Krumning optræder i mange sammenhænge: Kurver krummer, flader krummer, Universet krummer. Hvad mener man med det?  I indlæggene Smilehuller og rynker  og også Fra fladt papir til krumme flader, har krumning optrådt som en vigtig egenskab, så det er på sin plads med en uddybning:

Der er to væsensforskellige slags krumning: Indre og ydre. Den indre krumning kan man observere “indeni” ved at måle afstande og vinkler indeni. Uden at stikke hovedet op og kigge ud. Tænk for eksempel på en kugleflade, overfladen af en kugle. Den kan man kigge på udefra, og for eksempel måle radius og diameter, men indeni må man nøjes med at måle langs med kuglefladen. [Tilføjet januar 2018:  Der er tilsyneladende mulighed for at misforstå dette. Lad mig præcisere: Indeni betyder inde i den todimensionale overflade. Det er ikke som at være inde i en badebold, men at være inde i overfladen af badebolden. At være et meget fladt lille dyr, som ikke kan måle andet end langs med overfladen.] Selv med den begrænsning kan man godt observere, at der er krumning. Med Robert Ossermans æbleplantageanalogi (fra “Poetry of the Universe” dansk udgave: Universets geometriske poesi. link til bibliotekerne )

En æbleplantage i planen har æbletræer i lange lige rækker, og man kan plante dem med lige langt mellem træerne både på den ene og den anden led – man kan for eksempel sætte træer i et koordinatsystem – plante et træ hvor både x- og y-koordinaten er et helt tal.

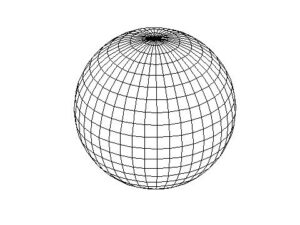
Lad os plante æbletræer på en kugleflade, hvor vi kun kan måle afstand og vinkler indeni fladen (strengt taget kan vi så ikke plante træer, for de stikker ud. Men lad os markere, hvor træerne skal stå.)

1. Man kan måle sig til at “gå ligeud” – langs en storcirkel. Hvorfor? Fordi storcirklen mellem to punkter er kurven, der svarer til at kortest afstand. Og vi kan jo måle afstand.
2. Vælg en storcirkel. Her vælger vi Ækvator: Plant æbletræer langs Ækvator med konstant afstand k.
3. Begynd i et af æbletræerne og gå vinkelret på Ækvator. Plant æbletræer med konstant afstand k langs storcirklen i den retning.
4. Gentag punkt 3 for alle æbletræerne langs Ækvator. Nu har vi plantet æbletræer langs alle længdegraderne.

Sådan en æbleplantage er fundamentalt anderledes end en æbleplantage i planen og det ses tydeligt på figuren: Hvis vi går op mod Nordpolen og kigger til siden, bliver der kortere og kortere mellem træerne. Da vi gjorde det samme i planen, fik vi samme afstand mellem træerne på begge ledder.

Det skyldes kuglefladens krumning. Nærmere bestemt Gausskrumningen.

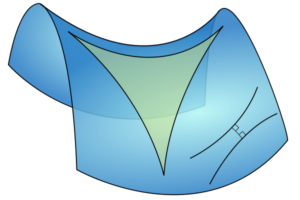
Plantageplantning på en cylinder har samme karakteristika som i planen, som figuren her viser. Man kan sætte træer efter et system, hvor afstandene på begge ledder holdes konstant. Forsøger man sig på en køletårnslignende flade (på figuren er den forrest), vil der blive længere og længere mellem træerne, når man går væk fra “mavebæltecirklen”.

Kuglen har positiv krumning, cylinderen (og planen) har krumning 0, køletårnet har negativ krumning. For flader med konstant krumning, kan man finde krumningen ved

1. Lav en trekant:  Vælg tre punkter og forbind dem parvis med den korteste kurve, som løber i fladen og ikke ud i rummet omkring. I planen er det linjer, på kuglen storcirkler og på køletårnet kan man forestille sig, at man sætter tegnestifter i punkterne og forbinder med elastiktråd, så elastiktråden løber langs køletårnets overflade og ikke ud i rummet omkring – det kan være svært at gøre konkret – elastikken vil meget let skyde genvej gennem rummet omkring. En tommefingerregel: Hvis den rette linje mellem de to punkter går ind i midten af køletårnet (hvis for eksempel punkterne begge to er på “mavebælteciklen”), så skal elastikken trækkes på ydersiden. Ellers skal den trække på ydersiden. (For eksempel for punkter lodret over hinanden på tårnet.) På tegningen nedenfor kan man se nogle eksempler på valg af punkter og forbindelser mellem dem på en køletårnsagtig flade.
2. Mål de tre vinkler a, b, c og arealet af trekanten, A. (Vinkler måles i radianer her.)
3. Da er a+b+c=+K*A. Og K er krumningen. Omvendt kan man få en formel for K ved at omorganisere ligningen. K=(a+b+c-)/A

Trekanter på “køletårnsagtige” flader (sadler, frisee-salat og kartoffelchips) har vinkelsum mindre end . På kuglefladen buler trekanter og får vinkelsum større end . I planen har de som bekendt vinkelsum . En torus har ikke konstant krumning – den har områder med positiv og områder med negativ krumning. Generelt varierer krumningen på en flade fra punkt til punkt. Og så skal man skærpe sin definition – det gør jeg ikke her.

Den ydre krumning er en effekt af, hvordan kurven, fladen,… er anbragt i et omliggende rum – hvor hurtigt den bøjer væk fra noget plant. I den forstand får en cylinder krumning og tynde cylindere krummer mere end tykke cylindere. Men set “indefra” kan man ikke observere denne krumning.

Når vi taler om, at universet eller rummet krummer, mener vi indre krumning. Man skal altså ikke forestille sig universet anbragt indeni noget endnu større.