I mandags, 20/3 2023, udkom et preprint “An aperiodic monotile“. Det gav anledning til megen aktivitet på diverse SoMe (i matematikerhjørnerne af SoMe inklusive vores egen FB-side) og i eksempelvis New Scientist. Det er et preprint – det betyder, at det ikke er udkommet i et tidsskrift endnu og at det ikke er igennem peer review, hvor andre eksperter læser det igennem og godkender, at det ser korrekt ud. Så der kan være fejl i, men nu får det alligevel et blogindlæg; forfatterne er i velanskrevne i området, så det er sikkert korrekt. Og der er fire forfattere; de kan nok korrigere hinanden. Nå, nok med forbeholdene. Hvad skal Einstein med en ny hat? Og hvorfor er det interessant.
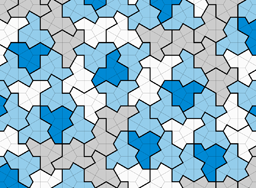
Hver flise i mønsteret ligner en hat. Det er en aperiodisk fliselægning. Billede fra forfatternes side om resultatet.
Hvad er en fliselægning?
Fliselægninger, tilings, af hele planen, er der mange af.





Eksemplerne her er periodiske: De bringes over i sig selv ved parallelforskydning.
En mængde fliser er aperiodisk, hvis:
- Man kan lave en fliselægning af hele planen ved kun at bruge disse fliser.
- Denne fliselægning er aperiodisk – ingen parallelforskydning bringer den over i sig selv.
- Man kan ikke med de samme fliser lave en periodisk fliselægning.
Den første mængde af fliser med den egenskab havde 20426 flisefaconer. Det var svaret på et spørgsmål i logik/datalogi, som var blevet oversat til et spørgsmål om aperiodiske fliser.
I 1974 lavede Roger Penrose, fysiker og Nobelprisvinder, et eksempel med 6 fliser:
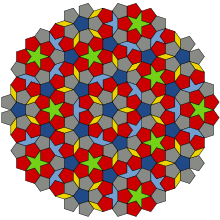
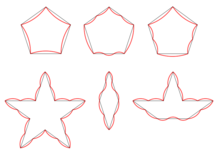
De mest kendte Penrose-fliser er “kite and dart”
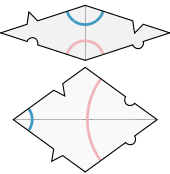
De røde og blå kurver har samme effekt – ligesom i et spil Tantrix.

Spørgsmålet, som den nye artikel svarer på, er, om der findes et eksempel med bare én flise. Vittige tyskkyndige har kaldt der “ein Stein”-problemet – heraf Einstein.
Svaret er nu ja, og flisen kaldes Einsteins hat… Ja, nørdhumor er sommetider ikke så avanceret. På hjemmesiden for artiklen er der interaktive illustrationer, en video om, hvordan man kan lave en hel kontinuert familie af disse aperiodiske hatte, og naturligvis link til artiklen.
Aperiodicitet fra periodiske mønster i højere dimension. (Kopieret fra tidligere blogindlæg – jeg er lidt doven lige nu)
Penrosemønstre og andre aperiodiske fliselægninger/byggeklodser kan konstrueres ved “cut and project” metoden. I 1981 viste B.G. de Bruin, at alle Penrosefliselægninger, som er lavet med små og store romber, kan konstrueres udfra standardgitteret i dimension 5, altså alle punkter (x1,x2,x3,x4,x5) i med heltallige koordinater ved
- Læg en plan ind i
,, så den ligger passende skævt – dens retningsvektorer skal have irrationale koordinater.
- Gør den lidt tykkere – gå et lille stykke ud vinkelret på begge retningsvektorer
- Projicer alle de gitterpunkter, der ligger i den optykkede plan ind på den oprindelige plan og forbind dem med kanter, hvis de var naboer i gitteret.
Det giver naturligvis et mønster i hele planen.

Hører man til dem, der ikke så let kan forestille sig to-dimensionale planer i det fem-dimensionale rum, er her et eksempel på at lave aperiodiske mønstre på en linje ved cut and project fra standardgitteret i planen.
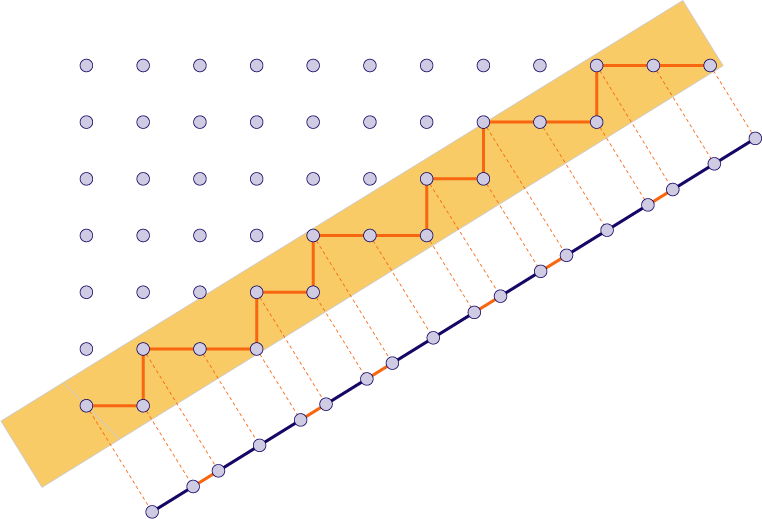
1D quasicrystals by Fibonacci substitution and lattice projection
Wolfram Community.
Bemærk, hvordan der er to forskellige linjestykker, som dækker, men man kan ikke parallelforskyde og få same mønster. Det opfylder ikke betingelsen om, at man ikke kan ommøblere og lave et periodisk mønster, men som sagt er det lettere at se en linje i planen end en plan i , og princippet om, at det porjicerede mønster er aperiodisk, kan vi godt se i eksemplet med linjen.
Billederne nedenfor viser en projektion af den 5-dimensionale kube vinkelret ind på en plan, som ligger skævt – altså punkter med koordinater (0,0,0,0,0), (1,0,0,0,0), (0,1,0,0,0),…,(1,1,0,0,0) ,… etc. op til (1,1,1,1,1) – der er 32 hjørner – og kanterne imellem dem. Der er taget flere hjørner og kanter med – punkter af typen (2,0,1,0,1,0). Det er jo hele heltalsgitteret, der er i spil. Det er vigtigt, at planen ligger skævt, da punkterne ellers havner oveni hinanden. (Tænk selv over det) Her er, så vidt jeg kan se, diagonale hjørner, der lander oveni hinanden – (0,0,0,0,0) og (1,1,1,1,1).
De hvide klatter er et mønster opdaget af kemikeren Schechtman i 1982. Det er bemærkelsesværdigt ved at have rotationssymmetri af orden 10, og det er der ingen periodiske krystalstrukturer, der har (jeps, det kan man bevise). Det var den første aperiodiske krystal-struktur – og det gav Nobelprisen mange år senere.
