OK titlen er på onkelhumor-niveau. Jeg kunne ikke lade være. Det, jeg vil fortælle jer om, er matematikken bag kortprojektioner, altså at lave en god repræsentation af (en del af) den runde jord på et kort, som jo er fladt.

Her ligger Svalbard.

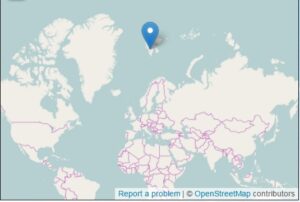
Da Politiken i december skulle vise læserne, hvor Svalbard ligger, brugte de dette kort. Det er rigtig nok, at Svalbard ligger der, hvor den blå pil er. Men det er alligevel ikke helt godt. Der er noget med størrelsesforhold: Svalbard ser ud til at være på størrelse med Storbritannien. I virkeligheden er Svalbard 61.000 km^2 og Storbritannien er 4 gange så stort.   Der er også et problem med retninger. Hvor kommer man hen, hvis man flyver stik nord fra Svalbard og fortsætter i den retning (stik syd, når man passerer Nordpolen)? Det kan man ikke se her – Nordpolen er strakt ud til en ret linje i dette kort.  Kortet er lavet i Mercatorprojektionen. Her kan man lege med arealer i Mercatorprojektionen.

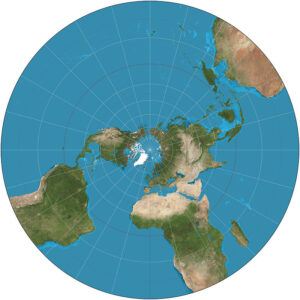
“Stereographic projection SW” by Strebe – Own work. Licensed under CC BY-SA 3.0 via Commons – 

Her er en anden fremstilling af, hvor Svalbard ligger. Det er lidt gnidret, men giver et bedre indtryk af, hvor områder tæt på Nordpolen ligger i forhold til hinanden. Man kan nu se, at en tur stik nord fra Svalbard vil ende et sted i Alaska. Der er stadig problemer med arealerne. Projektionen er en stereografisk projektion.

Google Earth. Nordpolen i centrum.

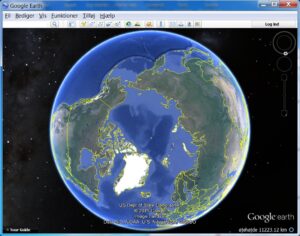
Google Earth giver et andet billede – men man får igen et meget bedre indtryk af områder tæt på Svalbard.

Hvad er så det bedste kort? Det er ikke så svært at indse, at man får problemer, hvis man vil vise hele Jorden i et enkelt kort. Man er i hvert fald nødt til at lave et hul et sted, før overfladen af Jorden kan strækkes ud i planen. (Hvis man vil ikke vil have flere punkter på Jorden til at ligge oveni hinanden i kortet.)

Her er den matematiske formulering af, hvad et kort er: Man kan give punkterne på Jorden geografiske koordinater (længdegrad, breddegrad)=. Et kort er så en funktion som tager to variable ind og giver to variable ud. For eksempel er Mercatorprojektion givet som 

Google Earth – kortet er sådan cirka 

Og Stereografisk projektion er

I alle tre eksempler, kan man skalere svarende til at squeeze på mobiltelefonen. Det svarer til at gange begge koordinater med en konstant (x,y) -> (kx,ky). Det ændrer ikke på de fundamentale egenskaber ved kortene. Nu kan vi regne på egenskaber ved kort og på et mere overordnet niveau spørge: Findes der kort, som opfylder xxx? Her er nogle spørgsmål og svar:

1. Findes der kort, der bevarer forholdet mellem arealer af landområder? Svar. Ja. (Se nederst for et eksempel)
2. Findes der kort, der bevarer vinkler? Svar: Ja. (Både Mercatorprojektion og Stereografisk projektion gør dette.)
3. Findes der kort med konstant målestoksforhold? Nej.
4. Findes der kort, som opfylder både 1 og 2? Nej.

3 og 4 siger, at der ikke findes et ideelt kort. Man må vælge det, der passer til formålet. Jeg vil ikke give et fuldt argument for 3 og 4 – det kan I jo komme til et af mine foredrag og høre om… Grundlæggende er problemet, at Jordens krumning forhindrer det.

Et kort argument for 3: Forsøg at lave sådan et kort med Nordpolen i centrum. lad os sige, det skal have målestoksforhold m. De punkter på Jorden, hvis afstand til Nordpolen er 50 km (afstand langs med Jordens runde overflade). skal i kortet have afstand km til punktet, der er f( Nordpolen). De ligger altså på en cirkel i planen med omkreds . Ser vi nu på den tilsvarende cirkel på Jorden, der altså udgøres af  punkter 50 km fra Nordpolen, når man måler langs Jordoverflade, så er dens omkreds mindre end . (Man går lidt “ind mod midten”, mens man går fra Nordpolen langs Jordoverfladen) Så skaleringsfaktoren langs denne cirkel er ikke målestoksforholdet m. Og altså er der ikke konstant målestoksforhold.

I Danmark har vi flere kort i spil. De er allesammen vinkelbevarende, da det er væsentligt for opmåling og gør, at “facon” bevares nogenlunde (og da man ikke kan få alting…): Mercatorprojektionen bruges til havområderne, og for landområderne har vi Transversal Mercator Projektion – Mercatorprojektion, hvor man først har drejet kuglen, så en længdegrad er lagt ned på Ækvator. Man skal vælge to ting: Hvilken længdegrad skal være i midten – midtemeridianen og hvad er variationen, afvigelsen fra hovedmålestoksforholdet  (målestoksforholdet er jo ikke konstant, men hvor galt må det gå) det fortæller implicit, hvor bredt kortet bliver. I Danmark har vi UTM med målestoksvariation og to zoner:  Zone 32 med midtemeridian og Zone 33 med midtemeridian  (Bredden på zonerne er altså til hver side. I virkeligheden bruger vi Zone 32 i hele landet undtagen Bornholm, men det er en anden historie.)

Vi har også DKTM, Dansk Transversal Mercator. Der er 4 Zoner med en målforholds afvigelse på maksimalt . DKTM har to zoner i Jylland. Kravet om lille variation af målestoksforholdet giver altså flere zoner, så man må vælge. Få zoner eller lille variation. Det er jo bøvlet at skifte kort 14 gange, når man skal køre fra Aalborg til Thisted, så det vil man gerne undgå.

I Danmark vedligeholdes kort af Geodatastyrelsen og der kan man også læse lidt om matematikken bag. Noget af det, de skriver, kan jeg kende fra mit eget kursus for landinspektørstuderende, men det har en hel generation af landinspektører også været igennem. Og de bliver jo også ansat i Geodatastyrelsen. Lige nu kan jeg faktisk ikke finde noget som helst om teorien bag kort, referencenet etc. på deres hjemmeside, men det er måske fordi de er ved at flytte hele molevitten til Aalborg, så de har nok at se til.

Archimedes’ arealbevarende cylinderprojektion,

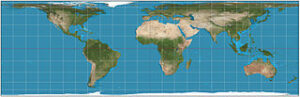
Her er en arealbevarende projektion. Som I kan se, er der problemer med faconen på områderne til gengæld.