For godt en uge siden, 7. januar 2016 annoncerede GIMPS, at de har fundet endnu et Mersenneprimtal, nemlig 274.207.281-1. Det plejer at give en avisnotits eller to, men faktisk er det ikke i sig selv særlig interessant, hvor stort det største kendte primtal er. Vi ved nemlig, og har vidst det siden Euklid, at der er uendelig mange primtal; eller sagt på en anden måde: Uanset hvor stort et tal, nogen giver mig, så ved jeg, at der er primtal, der er større end det.
Men det er da fascinerende, at man ved, at netop tallet 274.207.281-1 er et primtal. Det har 22.338.618 cifre i titalssystemet, så ja, det er godt nok stort.
Mersenneprimtal er primtal på formen 2p-1, hvor p i øvrigt også er et primtal. Ellers kan 2p-1 ikke være et primtal: Man kan nemlig faktorisere
, så hvis hverken r eller s er 1, har vi en faktorisering i ikke-trivielle faktorer.
Man kan sige mere end det, nemlig at primtal på formen altid har a=2 og p et primtal. Hvorfor? Jo, vi har lige set, at a-1 går op i
(brug s=1 og r=k i formlen ovenfor, og sæt a ind i stedet for 2) og hvis a ikke er 2 giver det igen en ikke-triviel faktorisering.
Altså er 74.207.281 også et primtal.
De første Mersenneprimtal er 3 (p=2), 7 (p=3), 31 (p=5), 127 (p= 7), 8191 (p=13) og de har været kendt i mere end 500 år. På Sloanes website med lister over heltal, som Ege har skrevet om her på bloggen, kan man finde en liste over primtal, som er eksponenter i Mersenne primtal. Den er nu ikke ajourført med det seneste i skrivende stund. Da man i 1963 fandt ud af, at p=11.213 giver et Mersenneprimtal, (det er det 23. af de 49 kendte Mersenneprimtal) lavede Illinois et særligt poststempel:

(Fra Eric Weissteins Mathworld)
GIMPS-projektet, Great Internet Mersenne Prime Search begyndte i 1996 som et af de første eksempler på “crowd sourcing” hvor mange stiller deres computere til rådighed for en større opgave. Det er interessant og senere brugt mange andre steder, at man på den måde fordeler beregninger til mange; og organiseringen af, hvordan man udnytter de mange mindre computere, er en opgave i sig selv – distribuerede beregninger er et område i datalogi.
Vi ved ikke, om der findes uendelig mange Mersenneprimtal, men med det seneste har vi da fundet 49. Hvis man vil finde meget, meget store primtal, så er Mersenneprimtal imidlertid et godt bud. Det er generelt svært at teste et stort tal for, om det er et primtal – og mere generelt at faktorisere et stort tal i sine primfaktorer. Men der er en test, Lucas Lehmer testen, som kun virker for tal på formen 2p-1, altså potentielle Mersenneprimtal, og som er hurtigere end andre tests for tal i den størrelse. Derfor kan det være smart at tage forholdsvis store primtal, som 74.207.281, (dem kan man finde ved en af de sædvanlige tests), og se om 2p-1 er et primtal. Og hvorfor vil man så finde store primtal? Tjah – af nysgerrighed, for at teste sin hardware, for at finde nye algoritmer til andre ting,… på “Why do people find these big primes?” er der en liste med 7 begrundelser:
- Tradition!
- For the by-products of the quest
- People collect rare and beautiful items
- For the glory!
- To test the hardware
- To learn more about their distribution
- For the money?
Jeg kan afsløre, at punkt 7 ikke er en hovedbegrundelse.
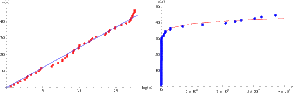
Om punkt 6 kan man sige, det er svært at lave formodninger, hvis man kun har 49 Mersenneprimtal, men på Mathworld er der en graf med antallet af Mersenneprimtal Mp=2p-1 med p < ln(x) (grafen til venstre på figuren). De finder bedste rette linje og skriver en anelse skeptisk: “If the line is not restricted to pass through the origin, the best fit is ![]() . It has been conjectured (without any particularly strong evidence) that the constant is given by
. It has been conjectured (without any particularly strong evidence) that the constant is given by ![]() , where
, where ![]() is the Euler-Mascheroni constant” Nu må vi se, om nummer 49 ryger langt ved siden af linjen.
is the Euler-Mascheroni constant” Nu må vi se, om nummer 49 ryger langt ved siden af linjen.
Når det er sagt, så bruges store primtal til kryptering, og det er helt fundamentalt i vores brug af netbanking og i det hele taget til hemmelig kommunikation over offentlige kanaler- Så jo, primtal er vigtige, algoritmer til at finde dem er vigtige, og ny information om primtal er altid fint.