Emmy Noether viste allerede i 1915, at fysiske bevarelsessætninger (energibevarelse, impulsbevarelse,…) alle har en symmetri af fysiske ligninger som underliggende forklaring eller i hvert fald makker. Så symmetri er ikke bare det, vi ser med det blotte øje i flisemønstre og havegange.
Matematisk set er en symmetri af en ligning eller en geometrisk figur, en afbildning (funktion), der ikke ændrer ligningen eller figuren. Eksempelvis er ligningen xy+yz+zx=2 uændret under ombytning af koordinaterne – en afbildning (x,y,z) -> (y,z,x) ændrer ikke ligningen. Den slags observationer kan være nyttige, når man skal løse ligninger – eksempelvis differentialligninger.
Jeg vil fokusere på geometriske figurer her, men der er altså mange andre anvendelser af symmetri. Symmetrierne af en geometrisk figur D i planen, er de funktioner fra planen til planen, som sender D bijektivt i sig selv
. Vi holder os her til isometrier, altså afbildninger f, som bevarer afstand mellem punkter:
.
Translationssymmetri: I sidste blogindlæg om kuglepakninger så vi på gitre. De har symmetri:
L= Alle punkter i planen, hvis koordinater begge er et helt tal.
f(x,y)=(x+1,y) og g(x,y)=(x,y+1) sender L over i sig selv og det gør alle afbildninger (x,y) -> (x+k,y+l), hvor k og l er hele tal.
Et gitter har samme type symmetri: Afbildninger
sender M i sig selv, når blot n og m er hele tal. Symmetrier, som er parallelforskydninger langs givne vektorer, kaldes translationssymmetri.
Rotationssymmetri.
Figuren her har rotationssymmetri: Hvis man drejer den med en vinkel på omkring midtpunktet, så går den over i sig selv. Det er ikke svært at forestille sig rotationssymmetriske figurer med vinkler på
for givet k.
Spejlinger I Folkeskolen lærer man om spejlingssymmetri. Det har vi naturligvis også med her: Man kan spejle i en given akse gennem origo. Desuden har vi glidespejlinger, som er spejling og translation i et hug. Det forstås vist lettest fra en tegning:  Spejling i aksen vandret mellem højre og venstrefødderne er ikke en symmetri, men kombineret med translation mod højre (eller venstre), er det.
Spejling i aksen vandret mellem højre og venstrefødderne er ikke en symmetri, men kombineret med translation mod højre (eller venstre), er det.
Matematikken bag:
Symmetrierne af en figur D udgør en gruppe med sammensætning af afbildninger som komposition: Hvis f og g er symmetrier, så
- er
en symmetri
er en symmetri
- identitetsafbildningen, i(x)=x er en symmetri.
Det er forbavsende, hvor meget, vi kan få ud af disse meget simple observationer. Altså, at vi nu har oversat til at studere grupper (og gruppevirkninger mere præcist). Gruppeteori er meget velstuderet og er helt centralt i matematikken – det er branchen “algebra”, der bl.a. omfatter gruppeteori.
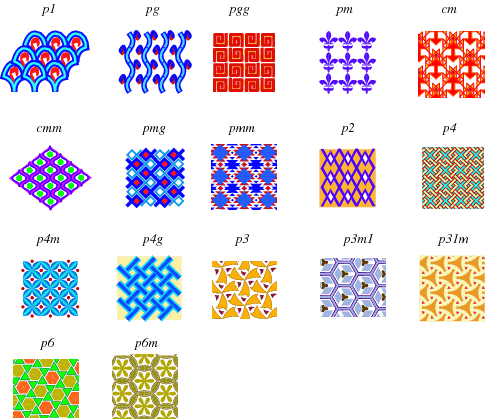
Tapetgrupper Tapetmønstre og fliselægning har en blanding af rotations, spejlings og og translationssymmetri. Som udgangspunkt kræves, at der er translationssymmetri i to retninger, i.e., langs to vektorer, som ikke må være parallelle – det ville være snyd. Nu spørger man så, hvis man er nysgerrig, hvad de mulige symmetrigrupper mon er. Det er (næsten) klart, at ikke alle kombinationer er tilladt. Roterer man med en vinkel, der ikke “passer sammen” med vektorerne, der skal translateres langs med, så går det ikke. Men det viser sig at være meget restriktivt. De grupper, der kan kombineres med translationer, er
- Cykliske grupper (rotationer) af orden 2,3,4 og 6 -(rotation med vinklen 360/2, 360/3, 360/4 og 360/6) og
- Diedergrupperne (som er rotation kombineret med en spejling – D1, D2, D3, D4, D6) Eksempelvis er D4, Diedergruppen med 8 elementer – (engelsk, dihedral group, hvis du vil Google) symmetrierne af et kvadrat – man kan rotere med vinklen 90 , 180, 270 og 0 grader og spejle i fire akser. D4 giver strukturen af sammensætning af rotationer og spejlinger.
Disse grupper er punktgrupperne – de holder et punkt fast. Og så er der tilbage at se, hvordan det kan kombineres med translationer:
Her er et mønster med tapetgruppe p31m. De blå pile er translationsretningerne. Der er spejligssymmetri og rotation med vinklen 120 graderomkring tre forskellige centre.

Tapetgruppen p3. Her er , ligesom for p31m rotationssymmetri med vinklen 120 grader, men her er ikke ikke spejlinger. Det forhindres af asymmetrien “indenfor fliserne”
Der er 17 væsensforskellige tapetmønstre. Her mener vi, at deres symmetrier er forskellige som gruppevirkninger og ikke nødvendigvis som grupper. Klassifikation kræver, at man overvejer, hvornår objekter er ens – der kan laves rigtig mange forskelligt udseende tapeter, som har samme symmetri. Det kan man lære mere om i projektet på 4. semester her på matematikstudiet. Figuren nedenfor viser dem alle 17. Der er en “grundflise”, som translateres i to retninger. Hvis denne grundflise ikke selv har nogen symmetri, er der kun translationerne og symmetrien af gittere. Har den symmetri, kan man lave en mindre grundflise, som flyttes rundt med både rotation/spejling og med translation. I eksemplet pm, er der en spejling udover translationerne. I p1, som i øvrigt ikke er tegnet helt færdigt, er der en asymmetrisk figur i “fliserne” – den forhindrer yderligere symmetri. I p6m er der rotation med vinklen og en spejling.
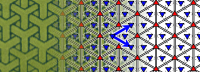
Der er en tilsvarende klassifikation af gittermønstre i rummet, hvor man forlanger tre translationsretninger. Det giver de såkaldte krystallografiske grupper. Dem er der 219 af. Ingen af disse grupper (tapet eller krystal) indeholder rotation med vinklen , som var symmetrien for Penrosemønsteret ovenfor. Og det er begyndelsen på et nyt kapitel, nemlig om kvasisymmetri.
Kvasisymmetri: Klassifikationen af de krystallografiske grupper har (selvfølgelig) stor betydning i kemi/fysik. Man ved, hvilke punktgrupper, (lokale symmetrier, som holder et punkt fast), man kan kombinere med translation – ligesom man ved det i planen. En af de grupper, man ikke kan have som punktgruppe, er Ikosaedergruppen – symmetrierne af ikosaederet. Og man kan som følge deraf ikke have rotation med orden 10 i et røntgendiffraktionsbillede (man sender røntgen eller muligvis andre stråler – jeg har kun bifag i fysik gennem et krystal og ser på det plane billede) af en krystalstruktur. Så Dan Schechtman blev meget forbavset, da han i 1982 så netop den rotationssymmetri i et
billede af Zn-Mg-Ho. Han blev så forbavset, at han endte med at få en Nobelpris. For at opdage kvasikrystaller. Kvasikrystaller er krystaller, som lokalt har en symmetri, som gentages – man genbruger en “3d-flise”, men gentagelsen er ikke en simpel paralleltranslation – der er ikke et gitter. Siden er der opdaget flere eksempler på kvasikrystalstrukturer i kemi. I planen er det tilsvarende spørgsmål: Kan man finde et antal fliser, som kan lægges i et mønster, der dækker planen, men som ikke kan lægges i et “tapetmønster”- altså periodisk i to retninger? Det kan man. Roger Penrose har givet navn til Penrose fliselægning og gav i 1975 et eksempel på 2 fliser, som kan dække planen, men ikke, hvis man forlange translationssymmetri. Billedet, jeg har brugt til at illustrere rotationssymmetri er del af en Penrosefliselægning. Billedet her viser fliserne foran Andrew Wiles-bygningen i Oxford. Det var et meget stor arbejde at få lagt fliserne og måtte gøres om, da nogle fliser ikke var lavet præcist nok.

Penrosefliselægning foran Matematisk Intitut i Oxford. Cirklerne er sat ind af kunstneriske årsager – af Penrose himself…