Mange store uløste matematiske problemer er meget svære at forstå. De drejer sig om matematik, som i sig selv er svært tilgængelig. Fermats problem er let at forstå. Men løsningen kan de færreste læse og forstå.
i denne uge har Popular Mechanics fem eksempler på problemer, som kan forklares, selvom vi ikke kan løse dem. Endnu. Det har jeg ladet mig inspirere af. I får to af problemerne her. Så må de andre komme senere – Cliff hanger…:
Om Euler-mursten og et problem, der ligner Fermat:
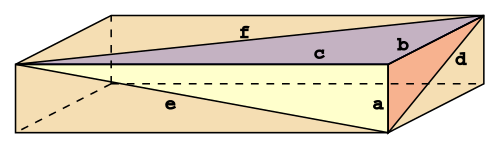
En Euler-mursten er en kasse, som opfylder
- Længde, bredde og højde er hele tal. a,b,c.
- Diagonalerne på sidefladerne er hele tal.
M.a.o. er a,b,c hele tal og det er løsningerne d,e, f til ,
og
også.
Der er uendelig mange tripler a,b,c, som er sidelængder i en Euler-mursten. Det mindste tripel er (a,b,c)= (44,117,240). Diagonalerne har da længde 125,244,267.
Når først, man har en løsning, kan man skalere med et helt tal og få endnu en. Derfor har vi allerede nu uendelig mange. Se Wikipedia for mange andre facts om Euler-mursten. Euler fandt to uendelige familier – som ikke bare var lavet ved skalering.
Nå, men det er tydeligvis ikke et uløst problem at finde Eulermursten. Men perfekte/fuldkomne Eulermursten har vi ikke fundet nogen af.
En Eulermursten er perfekt, hvis den opfylder betingelserne ovenfor. Og dens hoveddiagonal også har heltallig længde. Altså
3) og g er et helt tal.
VI ved ikke, om der findes perfekte Eulermursten. Vi har hverken dundet nogen eller vist, de ikke findes. Naturligvis ved vi, at der ikke findes nogen med små sidelængder. Det kan man sætte en computer til. Hvis der findes perfekte Eulermursten, er en af sidelængderne mindst (påstår Wikipedia).
OBS. Den skal BÅDE have heltallige sidediagonaler (d,e,f ovenfor) OG heltallig hoveddiagonal. I Popular Mechanics påstås, at vi ikke ved, om der finde heltallige løsninger til 3) I så fald skal jeg have skrevet en artikel om, at . Men det tror jeg nu alligevel ikke, jeg skal…
Sofakonstanten.
For en del år siden arbejdede projektgrupperne på 1.semester med “klaverflytning”. ( Som jeg husker det, var det Hans Huttels ide.) Hvor stort et klaver kan man få igennem en smal gang, der knækker? Det kom der fine projekter ud af – de fleste fokuserede på det plane problem, hvor man skubber klaveret rundt uden at måtte dreje det undervejs, de så på idealiserede klaverer – trekantede, kvadratiske, rektangulære,…
Leo Moser er efter sigende ophavsmand til Sofaflytningsproblemet: Hvad er det største areal, en plan figur kan have, hvis den skal kunne skubbes gennem en gang med bredde 1 og et 90 graders knæk. ( Det er underforstået, at gangen er lang på begge sider af knækket og at figuren er stiv.) Dette største areal kaldes sofakonstanten.
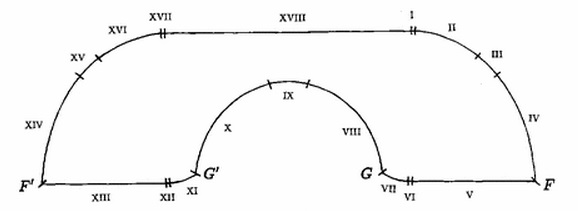
Jopseph L. Gervers sofa (fra 1991 – artiklen er her ) er bygget af 18 kurvestykker – antydet på figuren. Den har det største areal af alle de sofaer, vi kender, som kan skubbes gennem en gang som ovenfor.
Arealet af Gervers Sofa er ca. 2,2195. Det præcise tal og integralet, der regner det ud, kan man finde på MathWorld og i artiklen ovenfor. VI ved altså, at sofakonstanten er større end eller lig med arealet af Gervers sofa.
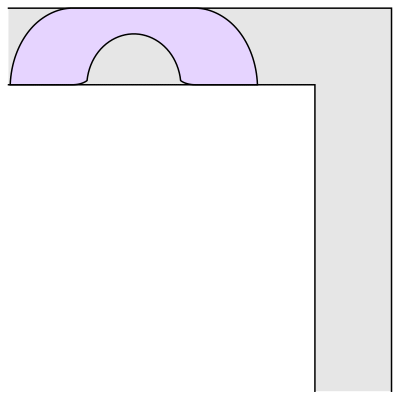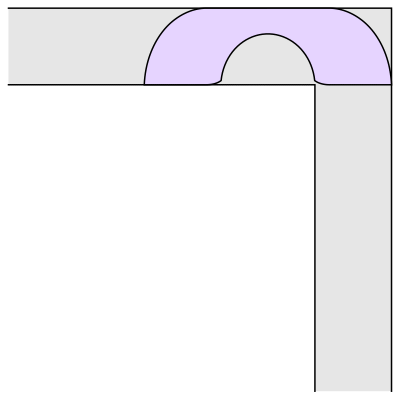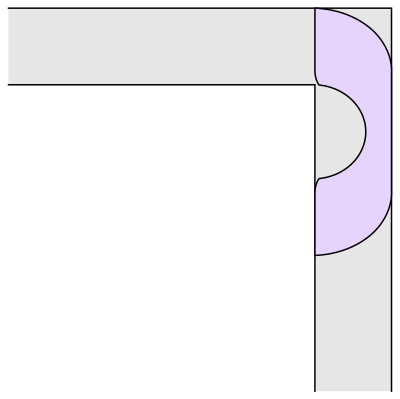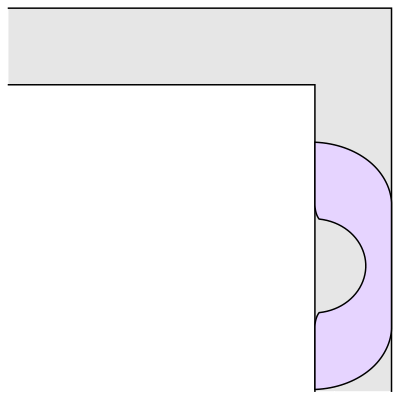
Gervers Sofa. Fra Dan Romik på UC Davis. Der er flere animationer og mere om sofaproblemet.
Mange matematiske geometriske problemer har “pæne” løsninger. Et område i planen, som kan hegnes ind af et hegn med længde L har størst areal, hvis det er en cirkel. Det tilsvarende problem i rummet giver en kugleflade. Så vi bliver lidt skuffede, når der er grimme løsninger. Og Gervers sofa er grim… 18 randkurver, hvor 3 er linjestykker og resten er løsninger til nogle differentialligninger, han opstiller. Det er ikke kønt. Før Gerver, havde vi Hammersleys sofaer:
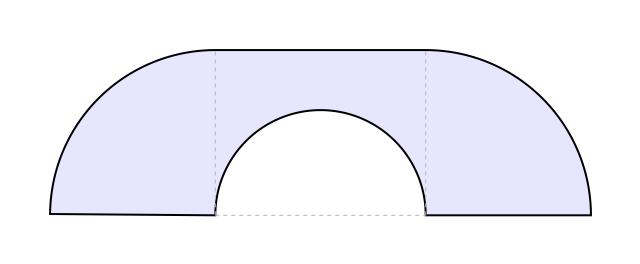
Hammersleys sofaer har, som man kan se, en halvcirkel i midten, to kvarte cirkler som en del af sofaryggen og linjestykker for resten. HAn konstruerede dem ved at lave en halvcirkel med radius 1 og sætte et rektangel ind i midten – det skal der så klippes en mindre halvcirkel ud af, hvis det hele skal kunne skubbes om hjørnet. Hammersley viste, at den facon er optimal, hvis den midterste halvcirkel, som er klippet ud, har radius . Det er egentlig en meget smukkere konstruktion end Gervers. Men arealet er
altså ca. 2,2074. Hammersley fandt også en øvre grænse for sofakonstanten på
(ca. 2,82). Jeg har ikke læst argumentet for det, så det vil jeg ikke udbrede mig om, men interesserede kan som altid Google.
Uanset, om den er grim vil det give ny indsigt, hvis Gervers sofa faktisk er optimal. Differentialligningerne, der indgår i hans konstruktion bygger på antagelser om en form for stabilitet af den måde, man skubber sofaen igennem. Måske er der ny viden at hente i disse antagelser.
Senere får I noget om Collatz-formodningen og den lykkelige slutning. Og måske også noget om indskrevne kvadrater.