Ved statsministerens pressemøde inden påske, hvor en gradvis “åbning” af Danmark blev lanceret, fortalte Kåre Mølbak fra Statens Serum Institut, at de har fremskrevet mulige scenarier ved at bruge matematiske modeller. I TV2News’ løbende undertekster stod “matematiske modeller” – altså med anførselstegn. Man kan se, at det er uvant, at der udtrykkeligt tales om matematiske modeller til et pressemøde…. selvom der er matematiske modeller bag valg af finansiering af stort set hvert eneste politiske udspil.

 

I Nature beder Julia Gog, britisk epidemiolog, om at slippe for, at for mange overfylder epidemiologernes inboxe og diverse preprintarkiver med halvbagte beregninger – hvis man virkelig vil hjælpe og har evnerne, vil det være godt at fortælle, hvad modellerne går ud på. Se det er et kampråb jeg kan forstå. Og reagere på.

Først lidt generelt om matematiske modeller: Det er modeller –  ikke virkeligheden. Når man laver en matematisk model vælger man at se bort fra noget af virkeligheden. Det gælder om

1. Modellen skal være simpel nok til, at man kan håndtere matematikken i den.
2. Resultaterne af at “regne” på matematiksiden skal være væsentlige og relevante for den virkelige problemstilling.
3. Output fra modellen skal kunne fortolkes, give mening og være nogenlunde retvisende for den virkelighed, der skal beskrives og påvirkes.

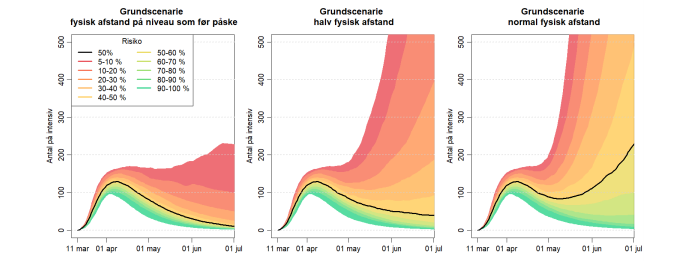
Hvor god modellen er afhænger i høj grad af, hvor godt man forstår den virkelig problemstiling, hvor meget og hvor præcist data, man har, hvor hurtigt, man kan få fat i data etc. Derfor vil output fra modeller ofte komme med flere mulige scenarier vægtet med forskellig sandsynlighed. Her er eksempelvis ekspertgruppens  prognose for indlæggelser på intensiv, hvis vi havde opretholdt restriktionerne fra før påske, men slækket på “social afstand”, som det kaldes.. Det går, som man kan se, ganske overordentlig meget galt med en ikke så lille sandsynlighed.

 

 

 

 

 

 

 

 

 

Hvor ved ekspertgruppen så det fra – hvordan laver de beregningerne? Hvad er modellen? Det får I ikke hele historien om – jeg er ikke epidemiolog – kan knap stave til det – men jeg kan løfte lidt af sløret – jeg har læst mig til noget og vidste lidt i forvejen.

Epidemimodeller. SIR og SEIR.

En meget simpel model for epidemier er SIR-modellen. Det er en kompartmentmodel hvor befolkningen er delt i “kasser” og flytter rundt mellem disse kasser. Her står S for Susceptible (de raske, der kan smittes), I for Infected (dem, der smitter), R for recovered (dem, der ikke smitter mere eller kan smittes). Man ser på en samlet population, som så enten er smitbare (S), smittede (I) eller (R):har været smittet, nu ikke smitbare og heller ikke smitter – herunder er også dem, der er døde.

S+I+R er konstant. Det er jo den samlede befolkning. Så Recovered inkluderer dem, der er døde.

Som tiden går flytter personer  mellem S, I og R. Det er altså funktioner af tiden S(t), I(t) og R(t).

HVordan flytter de rundt? Lad mig først udvide modellen til en SEIR, hvor E er Exposed – de er smittet, men smitter ikke endnu.

Hvor mange flytter fra S til E? Tiden kan her sættes til at svare til dage. Så hvordan udvikler S,E, R sig, hvis vi kender S(t), E(t), I(t), R(t) til et tidspunkt? Det afhænger af, hvor smittefarlig sygdommen er og hvor mange møder, der er mellem smittede og raske. Det plejer vi at modellere som en sædvanlig differentialligning (“sædvanlig” er et fagudtryk – “ordinary” er den engelske pendant –  S,E,I,R er funktioner af t, tiden og ikke andet – vi har nemlig også funktioner af flere variable):

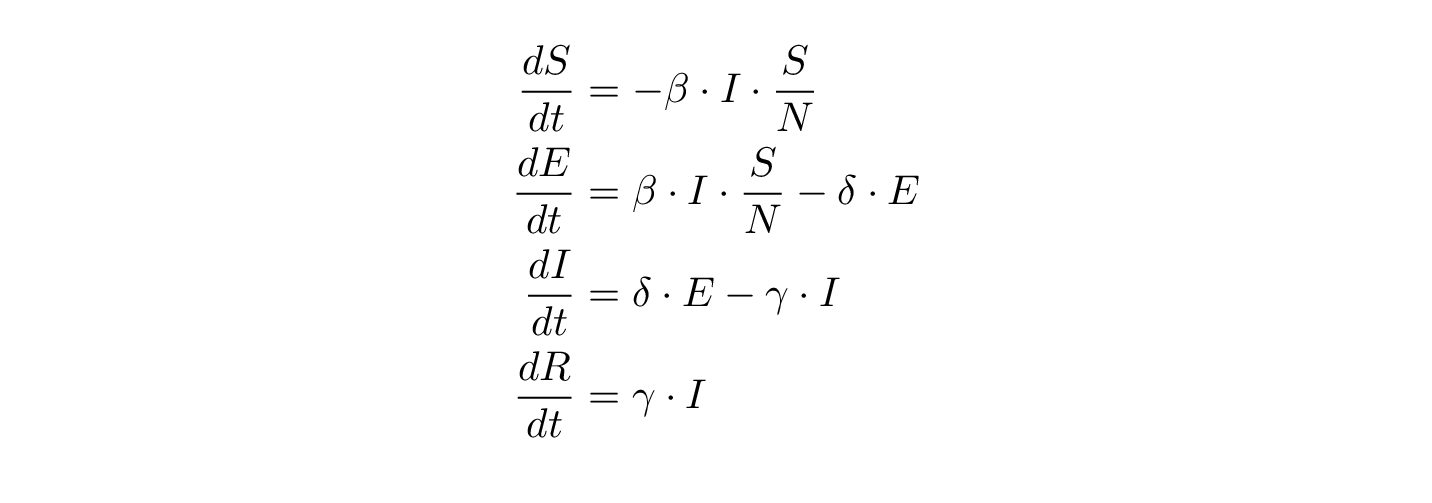
Lad mig starte nedefra:  , hvor D er det antal dage, man i gennemsnit er syg (og smitter) – det er altså den andel af de inficerede, der kommer sig og flytter til R. Den optræder (med modsat fortegn)  både i den afledte af R og den afledte af I – de flytter jo fra I til R. TIlsvarende er 1/d, hvor d er inkubationstiden – den tid, man er smittet, men ikke smitter.

er et mål for smitsomheden – den ganges med IS/N, hvor N er befolkningens størrelse – rationalet er, at man smitter, når man mødes.

Man kan allerede med denne model se, at det kan hjælpe på epidemiens udvikling at sætte syge i karantæne. Så bliver I(t) mindre  og der smittes ikke så mange.

Det er imidlertid en meget, meget simpel model. Hvis man skal lave de grafer, ekspertgruppen har lavet, skal man for eksempel vide, hvilken del at befolkningen, der bliver smittet – der er stor forskel på, hvor syg man bliver og dermed, om man skal på intensiv afdeling.

Det kan man reparere på ved at lave flere kompartments: Opdeling i aldersgrupper, som så er underopdelt i S, E, I, R, altså eksempelvis raske 0-5-årige. Det giver en finere model, hvor man kan tage hensyn til, hvilke dele af befolkningen, der mødes og dermed om de smittede 50-55-årige smitter de 0-5-årige.

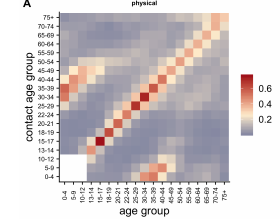
I England lavede man et “citizens science” projekt hvor 36.000 personer rapporterede om deres kontaktmønstre – hvem mødes de med og hvor (arbejde, hjemme, skole,…) Der var også automatisk indrapportering via GPS og telefoner. Ud af det kom eksempelvis kontaktmatricen nedenfor:

 

De hvide felter er manglende data – børn under 12 rapporterede ikke, eller der var ikke nok med.

Det giver en indikation af, at vi mødes med jævnaldrende og  børn mødes med deres forældre.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

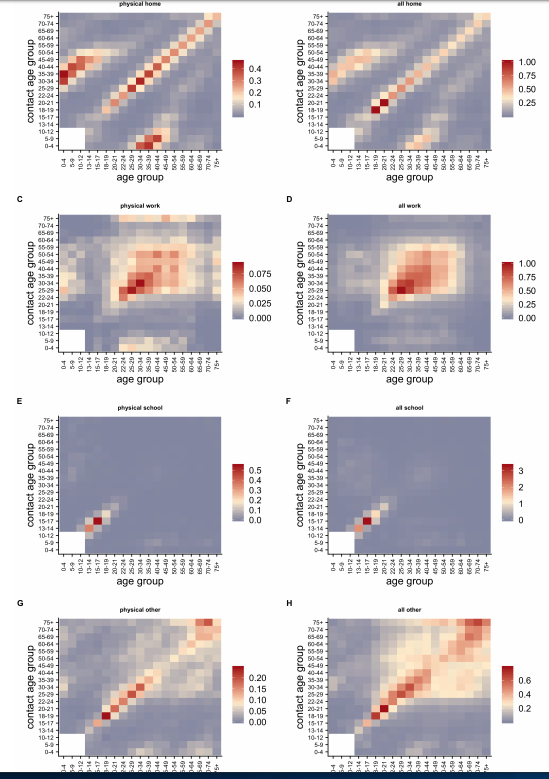
Hjælper det, at vi holder os hjemme? Det afhænger af, hvor vi mødes med hinanden og det har projektet i England også undersøgt. Søjlen til venstre er fysisk kontakt, til højre al kontakt – defineret passende – måske skal man tale med folk eller passere tæt på dem.

Det giver tydeligvis input til, hvad man får ud af at holde os hjemme fra arbejde. Desuden er fysisk kontakt minimeret ved “social distancing”. Man kan omvendt også se noget om, hvad det betyder at lade børn komme i skole.

Men, men: Det er en model for et land – Storbritannien. I Danmark er vores kontakter formentlig anderledes – i Storbritannien har de eksempelvis kostskoler, universitetsstuderende bor på universiteterne. De har færre vuggestuepladser og mange andre forskelle. Men uanset hvad: Man skal bruge viden om, hvordan og hvor vi mødes. Måske giver vi flere knus? Eller færre? (Det gør vi i hvert fald nu…)

Det er altså¨ganske indviklede modeller, men overordnet set drejer det sig om compartmentmodeller.

Den simple version, hvor befolkningen ikke underdeles efter alder, kan man læse mere om på dansk her. hvor kompartmentmodellen er udvidet med et Q for karantæne. Der er også mulighed for at “lege” med modellen. Men husk hele tiden, at det, der bruges af eksperterne, er mere kompliceret og i øvrigt skifter – man lærer mere om epidemien undervejs, kender antal syge bedre,…

Lige nu er AAU og DTU igang med en såkaldt agentbaseret model, hvor man simulerer enkeltindivider. På matematik her er det Torben Tvedebrink, Mikkel Meyer Andersen og Janus Valberg-Madsen, der er med i det projekt. Det kan være, de fortæller mere om det, men vi har jo egentlig ganske travlt med at holde universiteterne i luften med online undervisning.