Ja. Det kan man. Den findes allerede. Det er bogen Fermats Sidste Sætning, som er en billedbog lavet af kunstnergruppen Surrend og udgivet hos Dome of Visions. Surrendmedlem Jan Egesborg er også matematiklærer på Esbjerg Gymnasium og han har rådført sig med Johan P.Hansen, matematiker ved Århus Universitet, som har holdt en del foredrag om beviset for Fermats Sidste Sætning, FSS. (Der er noter og slides fra foredrag på siden).

Men måske er det slet ikke en børnebog om Fermats Sidste Sætning og derfor ikke et eksistensbevis? Selvfølgelig er beviset for Fermats Sidste Sætning ikke med i bogen. Det fylder godt 100 sider i Annals of Mathematics og kan end ikke læses af det store flertal af matematikere. Det kræver, at man er velbevandret i elliptiske kurver og algebraisk geometri, som er det område, beviset ligger i.

Bgoen blev anmeldt i Politiken

Jeg synes alligevel, det er en bog om Fermats Sidste Sætning. På samme måde, som børn kan lege med magneter og magnetisme, selvom magnetisme er en kvantemekanisk effekt og selvfølgelig ikke kan forstås af børn. Selvfølgelig kan børn ikke forstå beviset for Fermats sætning, men det, bogen gør, er at illustrere et modstridsargument. Der henvises på bagsiden af bogen til “Gerhard Freys smukke bidrag”. Frey konstruerede en elliptisk kurve hørende til et (muligvis ikke eksisterende) modeksempel til Fermats Sætning. Altså, hvis der findes naturlige tal a,b,c, så med n mindst 3, så findes en elliptisk kurve af en bestemt type. (Den er “ikke modulær”). Den kaldes en Frey-kurve.

Frey-kurven er en elliptisk kurve, hvis vi laver den udfra et modeksempel til FSS og den er “ikke modulær”. Det fører alt for vidt at definere elliptiske kurver – men i første omgang er det en kubisk kurve – ligningen er et polynomium i x og y og graden er 3. Man får et -led og ikke højere. Løsningsmængden (med x og y reelle tal) er en delmængde af planen – figurerne nedenfor er eksempler på kubiske og faktisk elliptiske kurver, taget fra Mathworld. Elliptiske kurver har en sammenhæng med komplekse funktioner, som er dobbeltperiodiske – der findes to komplekse tal , sådan at   for alle hele tal  . De to tal  må ikke opfylde hvor c er et reelt tal (eller omvendt – de er lineært uafhængige over de reelle tal), så punkterne  giver et gitter i den komplekse plan. funktionen f er altså bestemt ved sine værdier i et parallellogram og værdierne matcher langs kanterne. Folder man parallelogrammet sammen langs modstående kanter, får man en torus, så f er en funktion på en torus.

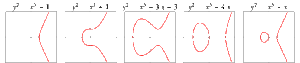
Elliptiske kurver fra Eric Wessteins Mathworld. Det får sort baggrund, hvilket formentlig kunne editeres værk, men I får lov at abstrahere i stedet for.

Frey indså, at hvis Taniyama Shimura Weil- formodningen er korrekt,  så findes der ikke nogen Frey-kurver. Fordi alle elliptiske kurver over de rationale tal ifølge Taniyama Shimura Weil  er modulære. Frey kunne ikke selv bevise dette, selvom han gav en del afargumenterne, så det tog flere matematikeres arbejde at få lukket hullet. Jean-Pierre Serre og Ken Ribet, nærmere bestemt. Da så Andrew Wiles beviste Taniyama-Shimura-Weil-formodningen, kunne han henvise til Frey, Serre og Ribet og konkludere, at Fermats Sidste Sætning er korrekt. Bemærk, at billedet af beviset for FSS som én matematikers arbejde – “the mathematical Marlboro Man” ikke er rigtigt.

I billedbogen indgår sådan en modstrid: Hvis der er en løsning, så er der et objekt (jeg vil ikke afsløre, hvad det er for et – I må jo låne bogen på biblioteket eller købe den), som man (tudsen på bogens forside) kan konkludere ikke findes. Jeg synes, det bliver lidt svært at være overbevist, når man tegner dette objekt – for så er det der jo allerede i en helt anden fysisk form end et abstrakt matematisk objekt såsom en løsning til FSS og en ikke-modulær elliptisk kurve – men det er rigtig fint at fortælle, at matematik indeholder den slags argumenter. Og forældre burde tale med børn om logiske slutninger og fejlslutninger. Der er nok af eksempler i hverdagen!