Tirsdag blev årets Abelprisvinder annonceret i en live streamet begivenhed i Oslo.

Karen K.Uhlenbeck får prisen for sit nybrudsarbejde (de skriver “nybrottsarbeid” på norsk) indenfor geometriske differentialligninger, gaugeteori og integrable systemer. Og for den fundamentale indflydelse, hendes arbejde har haft i analyse, geometri og matematisk fysik.

Her fortæller Karen Uhlenbeck om Emmy Noethers arbejde. (Foto Andrea Kane, IAS,Princeton) Noether var  i 1928 en af hovedforedragsholderne ved den internationale kongress for matematiker, ICM. Den næste kvinde i rækken af hovedforedragsholdere ved ICM var Karen Uhlenbeck i 1990.

Karen Keskulla Uhlenbeck (f. 1944) har, ligesom de andre Abelprismodtagere, haft en lang karriere i matematik og der er mange fine interviews og portrætter af hende på nettet. På Celebratio.org er hun  portrætteret i et fint interview af Allyn Jackson. Der er i øvrigt andre fine matematikerportrætter.

Jeg kender Uhlenbecks matematik fra da jeg i mit speciale beskæftigede mig med Gaugeteori. Uhlenbecks “bubbling” var helt centralt i det, der dengang var det hotte emne, 4-dimensionale mangfoldigheder og nye ideer, som forbandt forskellige områder af matematik og Gaugeteori fra fysik. Jeg vil (og kan) ikke forklare Uhlenbecks arbejde i detaljer, men nybrud, som Abelpriskommiteen kalder det, er en god overskrift.

Minimalflader, variationsregning og bobler/instantoner.

Minima og maksima for funktioner kendes fra gymnasierne. Man skal differentiere funktionen og finde nulpunkter.

Variationsregning er et skridt videre: Det, der skal minimeres er et funktional, som er en funktion, hvis input er andre funktioner. Det klassiske eksempel er det brachistochrone problem: Lav den hurtigste kuglebane mellem to punkter. Kuglen lægges i det øverste punkt og er kun påvirket af tyngdekraften, mens den ruller til det andet punkt. Man ville måske gætte på en linje – det er sådan en pæn kurve – men den blå kurve nedenfor giver svaret.

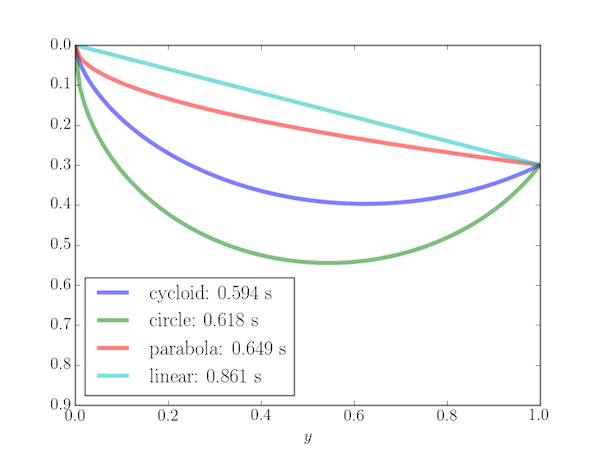
Man skal altså se på alle de kurver, der findes fra A til B – kurverne er de variable, funktionen er den samlede tid.

Mere generelt ser man på den samlede energi. Der er her vide rammer for, hvad energifunktionalet kan være. Man kan faktisk også her differentiere og finde nulpunkter for den afledede, men det kræver mere maskineri. Og man får bragt partielle afledede ind i billedet.

Uhlenbecks PhD-afhandling, “The calculus of variations and global analysis”, 1968, er i dette område.

Mens det brachistochrone problem drejer  sig om alle kurver mellem to punkter, kan man i stedet se på flader (2-dimensionale objekter) mellem givne randkurver (tænk på sæbehinder)

OBS: Det er ikke det, der er Uhlenbecks “bubbling”.

Man leder her efter fladen med mindst areal. Trækker man ringene langt fra hinanden, får man to sæbehinder – en i hver ring.

I det mere generelle problem, som Uhlenbeck og Jonathan Sacks løste, har man flader i mere komplicerede rum end vores sædvanlige Euklidiske. En flade er da en funktion fra kuglefladen til dette mere komplicerede rum. De konstruerer en følge af sådanne afbildninger, som allesammen er “pæne” og kommer tættere og tættere på en ny flade – en grænse for følgen. Matematikstuderende har set den slags grænsefunktioner i indledende analyse.

Grænsefladen er en funktion, som er pæn, bortset fra i et endeligt antal punkter, singulariteter. Tæt på singulariteterne har man “bubbling”. Arealet af grænsefladen er mindre end forventet – det er ikke grænsen for arealerne af følgen. Noget af arealet er boblet af – som et stykke tyggegummi.

Metoden og ideerne har haft enorm indflydelse – grænser, der kan kontrolleres, bortset fra i endelig mange punkter, er ikke så ringe endda. Og bubbling giver en forståelse af singulariteterne.

Gauge Teori

(udtales som en engelsk port, “gage”) drejer sig i fysik om de fænomener, som ikke ændrer sig, selvom man skifter “koordinatsystem” – laver en gaugetransformation. Fysikerne Yang og Mills fik i 1999 Nobelprisen for det, de i 1954 havde foreslået som en model for den svage vekselvirkning og som udvidede de hidtil brugte “koordinatskift” (til ikke-abelske grupper for de indviede).

Det, der skal være uafhængigt af valg af koordinatsystem er nogle partielle differentialligninger.

Invarians under koordinatskift – et simplere eksempel:

“Vindretningen er NNØ (Nord Nord Øst), hvor jeg står” giver kun mening, hvis jeg har et koordinatsystem med retningerne. Men vinden har den retning, den har.

Står man på Nordpolen, given NNØ ikke mening – der skal bruges flere koordinatsystemer for at beskrive retninger på Jorden, og tilhørende “oversættelser” fra et koordinatsystem til et andet.

Tilbage til Gaugeteori. Den kombination af partielle differentialligninger (Yang Millsligningerne)  og geometri (kugleflader, mere komplicerede flader og lignende højeredimensionale objekter – mangfoldigheder) kræver nye metoder og mod til at gøre noget i det ene matematiske område, som man aldrig har prøvet før. Uhlenbeck gav matematisk fast grund under fødderne i studiet af Yang Mills ligningerne. Bl.a. er bubbling fundamentalt. Uhlenbeck forklarer selv i interviewet med Allyn Jackson, at bubbling fungerer, når man har et problem, der er invariant under skalering – noget, hun allerede havde klarlagt i sin phd-afhandling.

Som den skarpsindige læser vil se, er Uhlenbecks arbejde ikke let at forklare. Hun har arbejdet mellem matematiske områder og kastet sig ud på det dybe vand imellem områderne.

Karen Uhlenbeck i Berkeley i 1969.

En anden side af Karen Uhlenbeck er hendes arbejde for at give matematikken videre. Hun startede, sammen med Dan Freed i 1996 Park City Mathematics Institute, PCMI, hvor bl.a. gymnasielærere og matematikere mødes. Det er flere parallelle sommerskoler og har haft stor betydning for mange, som er mødtes der. Der er en forskningsdel for phd-studerende og der er fokus på at give minoriteter i faget mulighed for at få fodfæste.

Karen Uhlenbeck har haft enorm indflydelse i både matematik som fag og blandt matematikere, og potentielle matematikere, hvor hun siger, hun håber, hun kan være rollemodel for de skæve eksistenser. Hun er rollemodel for mange, hun er en matematisk superstjerne og nu får hun Abelprisen. Det er jeg meget begejstret for.

Læs mere i Quanta Magazine  og på Abelprisens sider. Der er mange andre, men dem finder I nok, når I Googler.