Der er gang i de matematiske modeller lige nu. Og i at forklare og misforstå dem. Her vil  jeg give eksempler på gode forklaringer leveret af andre – der er ikke grund til at lave animationer etc. igen, når gode folk allerede har leveret dem. Og så vil jeg til sidst selv forklare et lille hjørne af den matematik, der er i spil. Matematikken indgår helt fundamentalt i at forsøge at forudsige, hvad der sker, hvis… Trods de matematiske modellers begrænsninger – der er mange forudsætninger og ting med småt, når man laver en model – så vil de fleste formentlig foretrække den slags modeller fremfor at spå i kaffegrums. Vejrudsigter gælder kun et stykke tid frem – det skyldes både begrænsninger i modellen og at man ikke kender data superpræcist. Sådan er det med alle disse modeller. Finasnministeriets modeller for økonomien i år havde eksempelvis ikke inkorporeret pandemien – så de gælder nok ikke nu.

Først lige et host om de mange fortolkninger og budskaber, som florerer med enten click bait intention eller ren og skær uvidenhed/manglende omtanke. (Jo, min titel med modelbureauet er lidt click bait, så undskyld for den 🙂 )

Min yndlingsoverskrift i den retning var “Flere kvinder end mænd testes nu positive for Coronavirus”  – det var en Ritzau-nyhed og stod i rigtig mange dagblade. Den kom et par dage efter, man var begyndt at teste rigtig mange, der arbejder i sundhedsvæsenet. Er der mange kvinder i sundhedsvæsenet? Joh, det er der vist. Så det er en ikke-nyhed, omend korrekt. Det forklarede en overlæge fra Seruminstituttet da også i artiklen, men overskriften skulle vi have.

Se den slags misvisende overskrifter og artikler skyldes egentlig ikke, at man mangler matematisk viden – de fleste kan forstå, at der er en sammenhæng mellem, hvilke grupper, der testes, og hvilke grupper, man finde syge iblandt. Andre skud i tågen skyldes mere, at man tror, man forstår matematikken og derefter selv laver udregninger bagpå en konvolut (hvis nogen har en konvolut…)

Meget afhænger af, hvem man tester. Mere om det nedenfor. (Lige nu, mens jeg skriver, kan man læse, at der skal testes “tilfældige danskere” – så er man fri for den skævvridning, der er i kun at teste bestemte grupper. Til gengæld skal man overveje det, der altid er i befolkningsundersøgelser – se for eksempel The problems of a “bad” test for antibodies. Hos Winton Centre for  Risk and evidence communication. Det er  ikke den test, man vil lave i DK lige nu, men testen for virus i svælget. Der gælder de samme overvejelser naturligvis. Udover overvejelser om, hvorvidt der er skævhed i, hvem der reagerer på en meddelelse i e-boks om, at man er udvalgt til at blive testet.)

Leg med tests og falske positive, falske negative på Understanding Uncertainty

 

Gode ressourcer om matematikken og modellerne.

I fredags, 1/5, gik siden, What Happens Next    i luften. Det er en imponerende flot side, det er lavet af Marcel Salathé, Epidemiolog ved EPFL Lausanne, og Nicky Case, som har stået for “art/code” og  på  ncase.me har  matematikanimationer/illustrationer under bl.a. overskriften explorable explanations. Det er rigtig godt lavet. Vil du oversætte til dansk, er det nemt at få lov til.  Jeg har bestemt mig til, at jeg ikke har tid.
Man kan eksperimentere med modellerne uden at få “ørerne i maskinen” og kløjs i matematikken. Men man skal selvfølgelig huske, at det er  modeller. Og, som Salathé har understreget fra det første offentlige foredrag, han holdt 26/2 om epidemien: Husk at checke datoen for et indlæg. Vi bliver klogere hele tiden. En hovedpointe i “What happens Next” er, at nedlukning af samfundet har givet os en mulighed for at starte forfra med at finde smittede, deres kontakter, isolere etc. Men gå igennem hele smøren, det er virkelig oplysende. De kalder det en epidemiflysimulator. Måske skulle nogen faktisk tage sig sammen og oversætte det…

En tidligere studerende på AAU, Michael Höhle, har på sin blog skrevet om grønne og røde kurver.

Onsdag 29/4 var der et Webinar arrangeret af ECMI (European Consortium for Mathematics in Industri) under titlen math4covid19. Her stå 4-tallet nok både for “for” og “against”. Der er mange tiltag i den retning, hvor vi forsøger at samle indsatsen. Det kan ses her. Det er på et noget andet matematisk niveau end ressourcen ovenfor, i.e., en anden målgruppe. Bl.a. fortæller Uffe Høgsbro Thygesen fra DTU om de modeller, vi bruger i Danmark. Man kan notere sig, at der er meget i spil. SEIR-modeller og kontaktstrukturer, som jeg beskrev i de to foregående blogindlæg, men naturligvis statistiske modeller oveni – tidsrækker, overlevelsesanalyse, stokastisk simulering af parametrene i modellerne, generelt en række modeller og ikke kun en enkelt. Som man må forvente det.

Det sidste foredrag drejede sig om at estimere, hvor mange, der er inficeret (i gruppen I i SIR-modellen). Det vil vi nu i DK gøre ved at teste en stikprøve af befolkningen. I foredraget estimeres det udfra dødstallet. Hvorfor? Jo, især når man vil sammenligne situationen i forskellige lande, om indsatser såsom lockdown virker etc., er effekten af forskellige teststrategier helt åbenlys. Hvis vi tester mange, finder vi mange. Og omvendt. Dødstallet kan så også være påvirket af, om man i et land ikke har ressourcer til at behandle de mest syge. Så der er ikke en facitliste. Se de sidste slides for alle forudsætningerne…

Dødelighed og overdødelighed.

Dødelighed og specielt overdødelighed monitoreres i Europa på EuroMOMO. Det er vores eget SerumInstitut, der står i spidsen for det. Man skulle tro, det var nemt nok at vide, om der dør usædvanligt mange, men det er det naturligvis ikke. Man skal vide, hvor mange, der plejer at dø, hvor stor spredningen er og i øvrigt, hvilken fordeling disse tal kan forventes at følge.

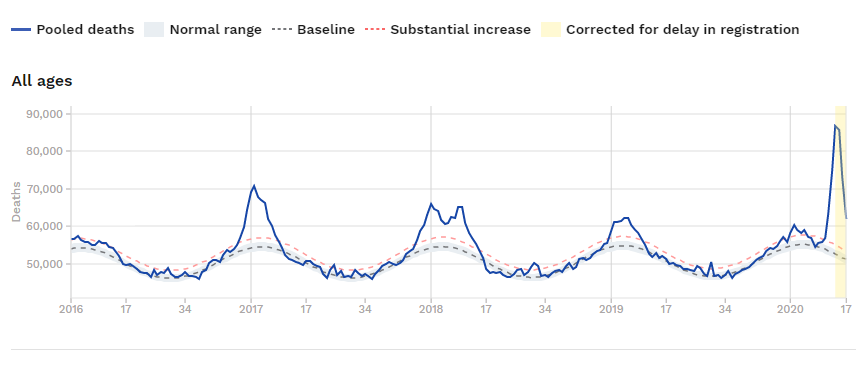
Her er det samlede antal døde – på ugebasis og siden 2016.

Bemærk de mange kurver. Den fede blå er data. Den stiplede blå “basislinje”, det grå normalområde, den stiplede røde for substantial increase og så det gule område til sidst, hvor man skal korrigere for, at tallene rapporteres senere end dødsdagen – forsinket henover weekenden eksempelvis.

Hvor kommer de andre kurver fra?

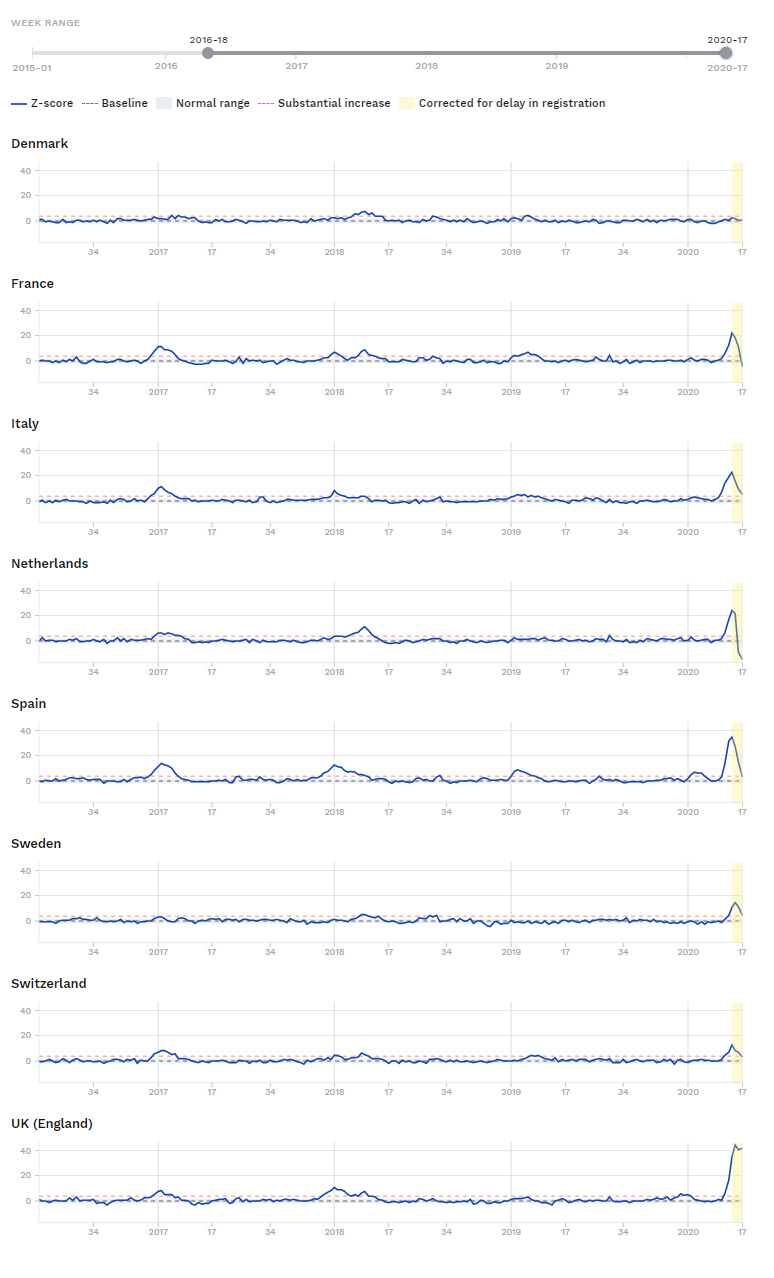
I får lige en hel masse andre kurver først (der er flere, hvor de kom fra på EuroMOMO)

 

 

 

De sidste kurver er “Z-score”, som, hvis man tager det med et gran salt, siger, hvor mange standardafvigelser, man ligger væk fra middelværdien i en normalfordeling. Mere end 3, hvor den stiplede røde kurve ligger – så er man substantielt over.

Men hvad så med det, der tilsyneladende sker ved årsskiftet – man ligger altid over den stiplede kurve i december. Så er det altså ikke et gennemsnit af dødstal i december et antal år tilbage. EuroMOMO skriver selv, hvordan de gør. Det er en Poissonfordelt tidsrække med trend og desuden en sinuskurve med året som periode. Modellen er altså mindre “hakkende” end gennemsnit af data. Det er med vilje. Man vil gerne kunne se, at der, som vanligt, er influenza ved juletid, eller se, at der nu her i april tydeligvis er det udbrud – men det ved vi jo.

Man kan tænke på en situation, hvor en model er en ret linje. Og der er flere data fra hver uge – fra flere år, hvor vi har samlet data til at lave modellen udfra. Så vil man nok ikke forvente, at den rette linje går gennem gennemsnit af data i hver uge.

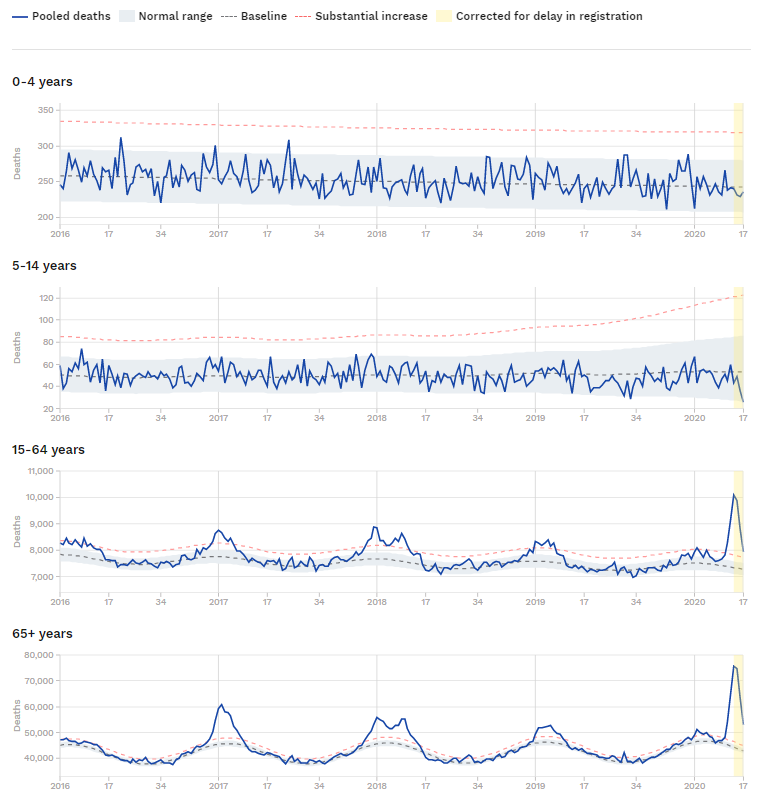
På den første graf kan man se, den stiplede kurve ligner en sinuskurve. Det skyldes, at man antager, at dødsfald blandt de 0-15-pårige ikke afhænger af årstiden, mens det for de over 15-årige er årstidsafhængigt – der dør flere om vinteren… så tilsammen afhænger det af årstiden, eftersom der dør flere over 15 end under. Det kan man se nedenfor, hvor døde i hele Europa er opdelt efter alder. Den grå stiplede kurve er en linje for 0-4 årige og for 5-14-årige. Den svinger for 15-64 årige og svinger mere for 65+