Matematikere i branchen algebraisk topologi vil sige, der er tre huller i en sædvanlig t-shirt. Andre vil nok mene, der er fire – to til ærmer, en halsåbning og et hul, hvor underkroppen stikker ud. Så hvorfor er matematikeren uenig i det?
Forklaringen på uenigheden er, at vi først skal definere, hvad et hul er, før vi tæller dem.

XKCD peger på et andet aspekt – i branchen Topologisk Data Analyse, ser vi på “huller” på forskellig “skala”, så kemikeren har også ret – det kommer vi til i en følgende blogpost – stay tuned. Men “normal person” har fat i noget, nemlig at der mangler en definition.
Lad os få t-shirten af vejen først: Der er et hul (af dimension 1) i et objekt, hvis man kan lave et loop (en lukket kurve for afficionados, se præcisionen nedenfor), som ikke kan trækkes sammen til et punkt, vel at mærke uden at den forlader objektet eller man klipper loopet over. Man må godt strække sit loop og skubbe det rundt undervejs – så trække sammen er lidt misvisende – deformere kunne man sige.

På en kugleflade (tænk på en badebold) kan alle loops trækkes sammen.
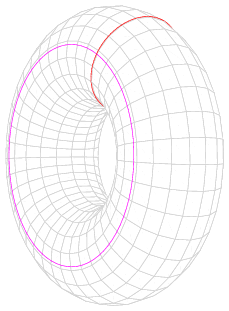
På en torus – en badering – den er hul indeni – kan man tegne (mindst) to loops, som ikke kan trækkes sammen til et punkt uden at trække dem udenfor torus.
(For de filosofisk anlagte: Hvis jeg laver et hul i badebolden, kan alle loops stadig trækkes sammen, så der er ikke noget hul i en badebold med et hul i – for topologerne…. Gisp!)
Så nu ved vi, hvornår der er ét hul og hvornår der ikke er nogen. På torus er der mange andre loops, der ikke kan trækkes sammen – man kan flytte lidt på det røde eller pink på tegningen, så får man tilsyneladende et nyt – men det gælder ikke.
Så hvordan tæller man loops?
- To loops betragtes som éns, hvis det ene kan deformeres over i det andet – ligesom vi trak et loop sammen på kuglefladen ovenfor.
- Man kan lægge loops sammen ved at sætte dem i forlængelse af hinanden.
- Det tæller ikke som et nyt loop, hvis man har taget to og lagt dem sammen. -Det svarer til lineær uafhængighed i lineær algebra.
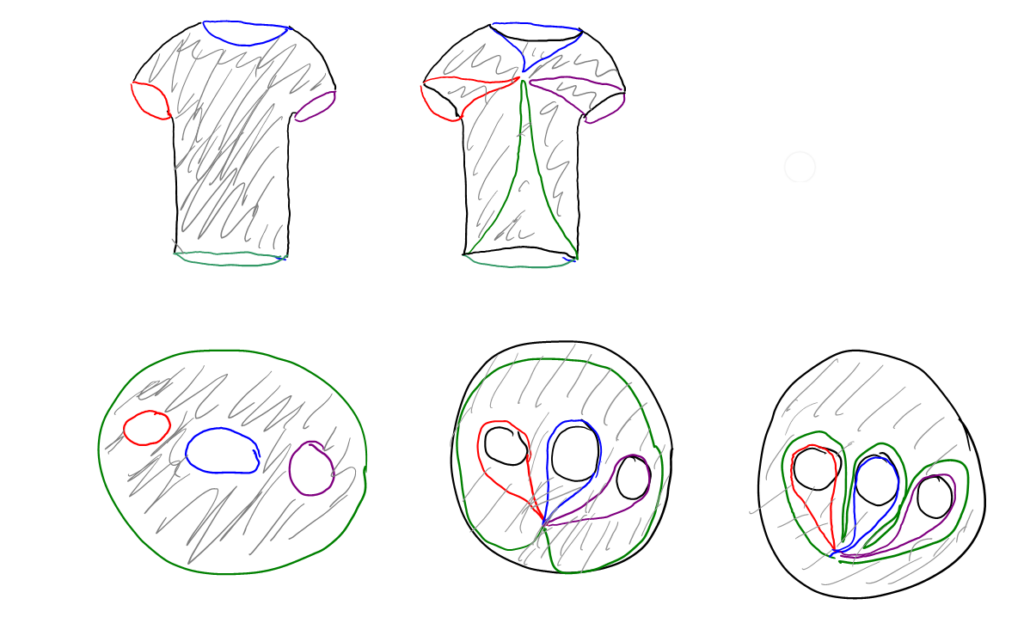
Antallet af huller (af dimension 1) er antal loops, når man tæller som beskrevet i de tre punkter. I figuren kan man se fire loops på en (grå) t-shirt. De deformeres, så de allesammen går igennem et fælles punkt. Det er “de samme” fire loops ifølge 1) ovenfor. Nedenfor har jeg trukket t-shirten ud og lagt den fladt – ellers er det svært at se bagsiden, og der er stadig samme loops, så det er ok. Den sidste fladmaste figur viser det grønne loop trukket sammen til at følge det røde loop, derefter det blå og så det lilla. Det grønne er altså en sum af de tre andre. Derfor er der tre huller i en t-shirt.
Andre typer huller
Der er andre typer af huller – torussen ovenfor har et hulrum indeni, og det har badebolden også. Det er huller af dimension 2 – fordi der sidder noget 2-dimensionalt rundt om, ligesom hullerne i t-shirten blev fundet via (1-dimensionale) loops.
Med matematik – loops og sammentrækning
Man kan naturligvis beskrive et loop præcist med matematik: Her er X badebolden eller torussen eller noget andet, man vil undersøge, og
er intervallet fra 0 til 1.
skal være kontinuert.
Man kan trække/deformere en lukket kurve over en lukket kurve
hvis der er en fri homotopi:
så
,
for alle s, og
. H skal være kontinuert.
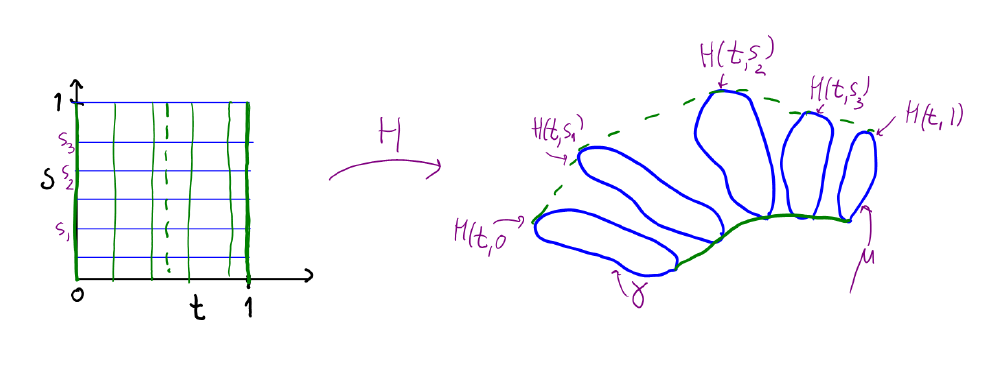
Hvordan kan jeg vide, hvordan jeg skal deformere loops? Og om det kan lade sig gøre? Hvordan kan man regne på geometrien? Det kan man bestemt heller ikke altid, men hvis man kan dele sit objekt op, kan det hjælpe.
Trekanter, tetraedre, polyedre, huller og hulrum.
Hvis man har et objekt, der er opdelt i linjestykker, trekanter, tetraedre og højeredimensionale tilsvarende objekter – simplices hedder de – så kan man regne på huller – både dem i t-shirten og dem, der er hulrum i badebolden og torussen. Der er et par kameler, der skal sluges i forhold til t-shirt-eksemplet med kurver og deformationer.
(For den indsigtsfulde læser går vi her fra homotopi til homologi – en ret heftig kamel 🐫at sluge, men hvis man ikke ved, der er en kamel, glider den lettere ned.)
- I stedet for at tillade alle mulige loops, kan man nøjes med dem, der er sammensat af linjestykker.
- I stedet for at spørge, om et loop kan deformeres til et punkt, spørger man, om det kan fyldes ud med trekanter. I så fald er dette loop 0.
- To loops er “ens”, hvis man kan fylde ud imellem dem med trekanter.
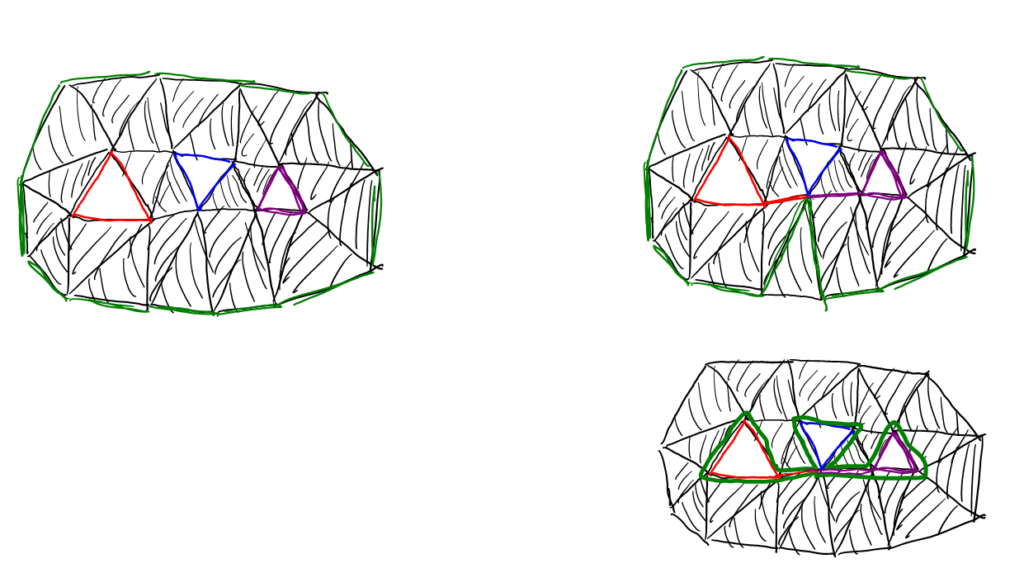
På figuren er lavet samme loops som i tegningen før, men man må kun bruge linjestykkerne – det røde er derefter forlænget med et linjestykke til spidsen af det blå; man går altså ad den kant og tilbage. Det lilla ligesådan. Det grønne er i første omgang flyttet henover en trekant; det må man godt. I den sidste tegning er det grønne flyttet henover mange trekanter og blevet til en sum af de tre andre.
Men synspunktet er nu faktisk et andet:
Rundt om en grå/skraveret trekant er et loop – via de tre kanter. Det loop er 0 – det er fyldt ud med en trekant.
Hverken det lilla, blå, røde eller grønne er nul hver for sig – ingen af dem er fyldt ud med trekanter. Men vi kan kombinere dem. Den figur, vi får ved at se på alle de grå trekanter, har en kant/rand, som er det røde plus det blå plus det grønne plus det lilla. Så den sum er nul.
rød + blå + grøn + lilla =0
Endnu en kamel: Vi holder ikke styr på, om man løber den ene eller den anden vej rundt – det gør, at ligningen ovenfor også kan skrives eksempelvis
rød = blå + grøn + lilla
rød + blå = grøn + lilla
grøn= rød+ blå + lilla
Den sidste svarer til det, vi gjorde tidligere, altså at det grønne loop er en kombination af det tre andre.
På samme måde kan man se på andre typer “huller”. Hvor et loop dannes af kanter/linjestykker, som hænger sammen med hinanden – altså ikke har nogen frithængende ender, så er et hulrum dannet af trekanter, der ikke har frithængende sider/kanter. Trekanterne på torussen nedenfor mødes to og to langs kanter. De omslutter et hulrum. (Og ja, det er voldsomt mange trekanter…). Hvis jeg fjerner en trekant (uden at fjerne dens kanter), er dens tre kanter nu frithængende og der er ikke et hulrum indeni.
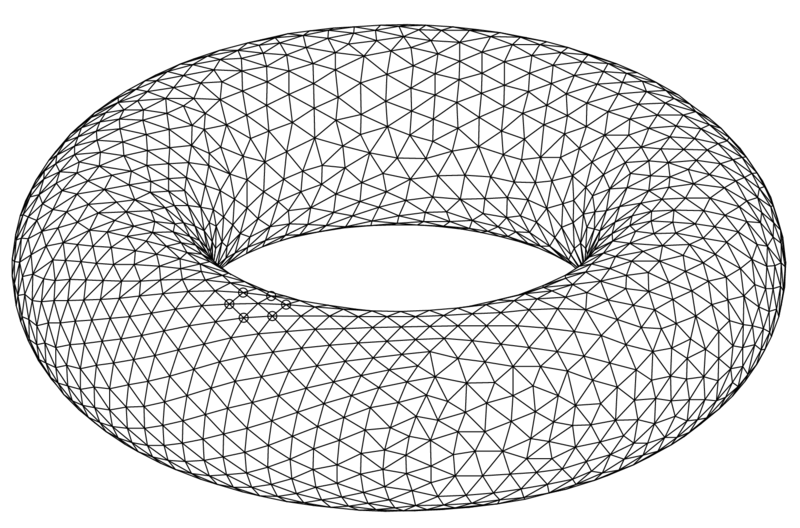
Algebra og udregninger
Algebraen bag kommer via trianguleringen, som beskrives som en sammenlimning af punkter linjestykker, trekanter, tetraedre, ,etc. hvor man har styr på, hvilke punkter, der er endepunkter for hvilke linjestykker, hvilke linjestykker, der er kanter i hvilke trekanter, hvilke trekanter, der er sideflader i hvilke tetraedre etc. Sætter man det i system, kan man bruge (smart) lineær algebra til at regne på huller af forskellig dimension. Hvis man tæller huller som ovenfor – antal huller af dimension k er udregning af dimensionen af et vektorrum – så får man – hvis vi holder os til at bygge med punkter, kanter, trekanter og tetraedre, at
antal punkter – antal kanter + antal trekanter – antal tetraedre = antal sammenhængskomponenter -antal huller af dimension 1 + antal huller af dimension 2 – antal huller af dimension 3.
Det tal kaldes Eulerkarakteristikken af det objekt, man har bygget. For en kugleflade er Eulerkarakteristikken 2. Der er 1 sammenhængskomponent (alle punkter på kuglen kan forbindes til hinanden), 0 loops og dermed 0 huller af dimension 1, 1 hul af dimension 2 og 0 huller af dimension 3.
For torussen er tallet 0. Der er 1 sammenhængskomponent, 2 loops, 1 2-dimensionalt hul. Det betyder også, at de vildt mange trekanter på den triangulerede torus opfylder
Antal (hjørne)punkter – antal kanter + antal trekanter =0
Og det behøver man ikke tælle efter. Det afhænger ikke af, hvordan man har opdelt i trekanter.
I geometrikurser møder man Eulerkarakteristikken af en lukket flade som den samlede Gausskrumning.