I blogposten Der er tre huller i en t-shirt lovede jeg, at vi skulle se på huller i forskellig skala. Zoomer man meget ind på en t-shirt, er der masser af huller igennem det materiale, det en strikket af, så der er tydeligvis flere svar på “hvor mange huller”.
I den tidligere blogpost gik jeg ud fra, at materialet var noget helt uden små huller, og det er det jo aldrig – ikke for en kemiker eller fysiker. Det viser sig at være vældig smart – hvis man tager det alvorligt og bruger persistent homology. Persistent kan betyde vedholdende, vedvarende eller ihærdig og her er det nok mest vedvarende, man skal tænke på.
Her er først opskriften på at komme fra atomers placering til noget med huller/loops/homologi. Tegningen nedenfor er i 2d, fordi det er lettest at tegne.
Man starter med de 12 punkter. Så lader man kugler vokse med centrum i punkterne – større og større radius. Undervejs holder vi øje med, om kuglerne mødes.
-
- Når to kugler mødes indsættes linjestykket mellem deres centre.
- Når tre kugler mødes – ikke bare parvis – indsættes en trekant (hele trekanten, ikke kun dens kanter.)
- Når fire kugler mødes, indsættes et tetraeder – ikke kun overfladen, men hele tetraedret.
Det giver en figur bygget af punkter, kanter, trekanter, tetraedre, som i forrige blogpost
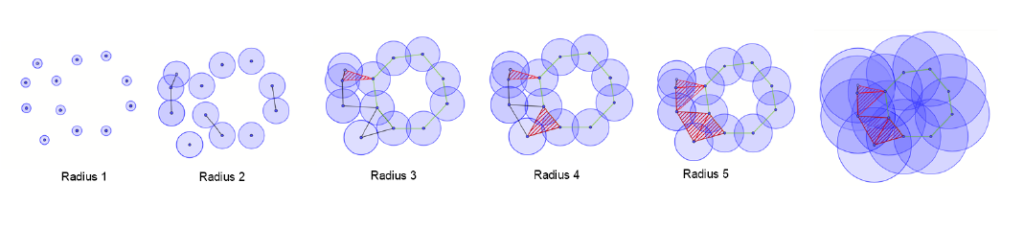
Undervejs opstår huller af dimension 1 (der er loops), de bliver fyldt ud med trekanter, når kuglerne er vokset mere. Man siger, de fødes ved en vis radius og dør ved en anden. Det holder man styr på, og tæller rigtigt – husk, der er (kun) tre huller i en t-shirt.
For hvert loop har man to tal, fødselsradius og dødsradius. Det giver et punkt (fødsel,død), som på grafen her
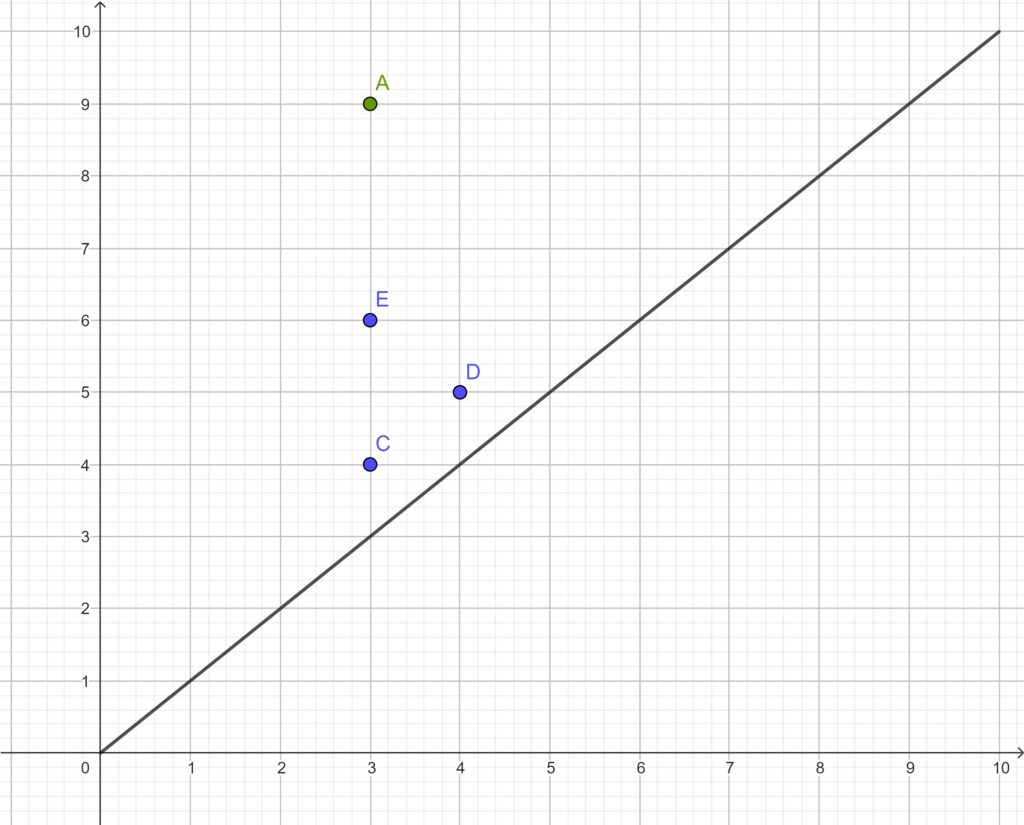
Der fødes et loop ved radius 4, som dør ved radius 5.
Man kunne finde mange andre loops undervejs, men de er talt med, som vi så med hullerne i t-shirten.
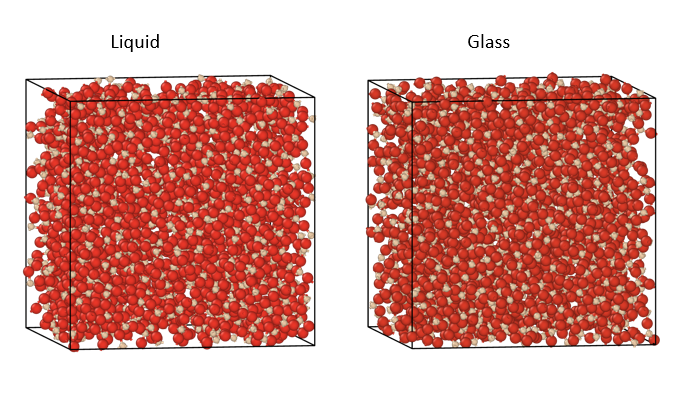
Hullet, der lever længst, A, er, når man kigger på punkterne, nok det med overbevisende hul, men i kemi vil vi gerne kende både små og store huller, altså på forskellig skala. Hvordan ser man f.-eks. forskel på glas og væske? Det er ikke let med det blotte øje. Billederne viser resultatet af simulering af glas og væske i en (stor) computer. Det er derfor, vi ved, hvor atomerne sidder:
Nedenfor har vi udregnet persistent homology og sat punkter svarende til loops ind i et koordinatsystem. Man kan godt se, der er en forskel på væske og glas i de diagrammer. Det kan kemikerne kigge nærmere på,
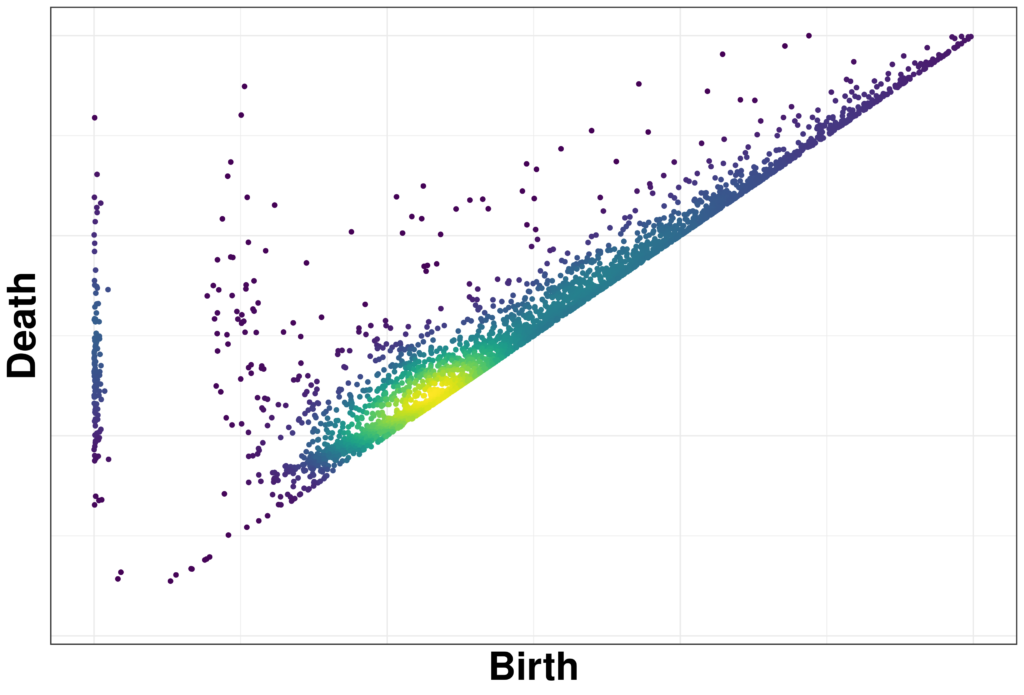
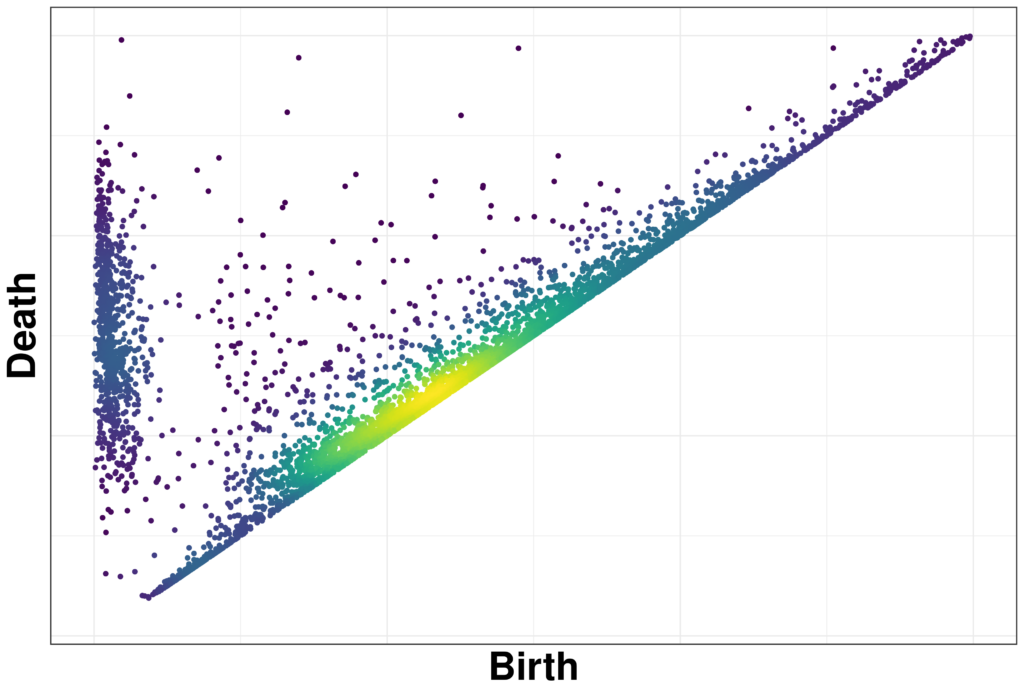
Vi kan sammenligne disse persistent diagrammer, som de hedder, ved for eksempel at bruge Machine Learning. Vi kan se på forskellige typer glas og vi kan selvfølgelig se på meget andet end glas – der er meget data, der kan betragtes som punkter, lige som centrum for atomerne. Det kan endda være punkter med mange koordinater.
Så kan man gå fra datapunkter -> Persistent diagrammer -> sammenligninger via Machine Learning.
Det kaldes Topologisk Data Analyse, TDA. Man bruger selvfølgelig også “huller” af højere dimension – hulrum – og laver diagrammer for, hvornår de fødes og dør.
Lige nu kigger vi efter tunneler gennem glas. Det kan man godt tænke på, som huller af dimension 1 – i den 2d-figur, jeg har lavet med voksende kugler, kunne man forestille sig, at det var en 3d-glasstruktur, hvor man kigger gennem hullerne -svarende til at kigge gennem en tunnel… hvis læseren kan se det for sig. Det viser sig at være noget mere indviklet at beskrive tunneler, så det giver mening i kemi, men så er der jo noget at tænke over. Det bliver det kun mere interessant af.