Abelprisen går til Yves Meyer.

Morten Nielsen har skrevet om årets Abelpris – og Arne Jensen har tidligere skrevet om Wavelets. Tak for det! – tilsammen giver det:

Abelprisen 2017
går til Yves F. Meyer (billede B. Eymann, Académie des Sciences)

for hans væsentlige bidrag til teorien om wa-
velets. Wavelets er funktionsystemer, der fremkommer ved dilatering
(udstrækning) og translation af én fast funktion :

$\psi$ :
$\{2^{j/2}\psi(2^jx-k)\},$

hvor j og k gennemløber heltallene. Langt de fleste funktioner frem-
bringer “ubrugelige” systemer, men tilbage i 1909 observerede Alfred
Haar at funktionen

$\psi(x)$ =

$1 \;\mbox{for}\;0 \leq x < \frac{1}{2},$
$-1 \;\mbox{for}\; \frac{1}{2} \leq x < 1,$
$0\; \mbox{ellers.}$

giver et såkaldt ortonormal system, der kan benyttes til at dekomponere
alle “rimelige” funktioner.
Haars funktion er ikke specielt “pæn”. Den er f.eks. ikke kontinuert
og det blev længe betragtet som en nær håbløs opgave at finde bedre
frembringere . Desuden kunne ingen på daværende tidspunkt forestille
sig praktiske anvendelser af sådanne systemer. Faktisk skulle der gå
omkring 70 år fra Haars opdagelse indtil tiden (og teknologien) var
moden til næste skridt.
Omkring 1980 kom geofysikeren Jean Morlet frem til, at systemer
med samme struktur som Haars system, ved implementation på en
computer, tilsyneladende var meget effektive til brug ved analyse af
seismografudskrifter fra olieeftersøgning. Dog havde Morlet ingen teo-
retisk forklaring på observationerne, men Morlets resultater satte gang
i intens ny forskning indenfor området.
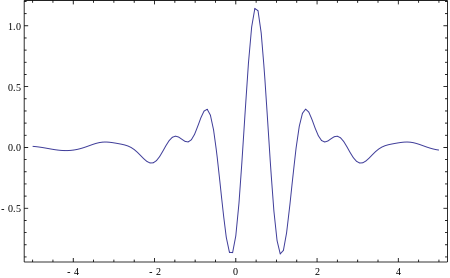
Nogle af de vigtigste fremskridt stod Yves Meyer for. Meyer kon-
struerede sammen med P. G. Lemarié-Rieusset det første eksempel på
en glat ortonormal wavelet, og Meyers analyse af konstruktionen ba-
seret på Fourieranalyse førte til en fuldstændig beskrivelse af glatte
wavelets. (Grafen viser Lemarié-Rieusset og Meyers wavelet – funktionsudtryk kan man finde her)

Wavelets anvendes i dag til mange ting, for eksempel kompression af
musik, billeder og video. Der er bl.a. en nyere standard for billedkom-
pression (JPEG2000) som er baseret på wavelets.
Yderligere information om wavelets kan f.eks. findes i denne tekst
skrevet af Arne Jensen til Numb3rsbloggen.