Rygterne går blandt matematikere og dataloger. Det ser ud til, at Laszlo Babai på tirsdag vil holde et foredrag om et stort resultat: Her er annonceringen Title: Laszlo Babai (University of Chicago): Graph Isomorphism in Quasipolynomial Time (Combinatorics and TCS seminar)
When: Tue Nov 10, 2015 3pm to 4pm  CST
Where: Ry 251
Description: We outline an algorithm that solves the Graph Isomorphism (GI) problem and the related problems of String Isomorphism (SI) and Coset Intersection (CI) in quasipolynomial (exp(polylog n)) time. 

Babai holder tre foredrag (i aftes, da jeg begyndte at skrive dette indlæg, var der kun annonceret et foredrag, men de har nok insisteret på at få en længere historie).

Hvad går det ud på? Vi skal have to ting på plads, nemlig grafisomorfier og quasipolynomiel tid.

Graf-isomorfi-problemet:

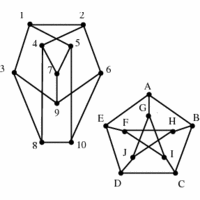
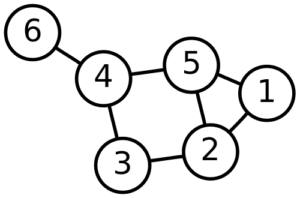Her er en graf. Den består af nogle knuder (de runde bobler) og nogle kanter (linjestykkerne imellem).

To grafer er ens, isomorfe, hvis man kan matche knuderne i den ene med knuderne i den anden og samtidig få kanterne til at passe sammen. OBS: Det er ikke det samme som dette problem,.

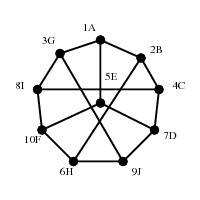
Her er to grafer, som faktisk er isomorfe. Det kan man måske ikke lige se, men på grafen nedenunder er skrevet en matching af knuderne ind (ved hver knude står navnet på en knude fra hver af de to grafer) og kanterne passer.

Når man har et forslag til en isomorfi kan man checke, om det faktisk er en isomorfi, og det er let nok. Men at finde en, eller bare vide, om der findes en, er straks værre.

Grafisomorfiproblemet går ud på at lave en algoritme, som kan undersøge, om der findes sådan en matching af to grafer. Men udover det, og det er det interessante: At bestemme, hvor god en algoritme, det er muligt at lave. Altså, hvor mange skridt en algoritme, der løser dette problem, mindst skal bruge som funktion af størrelsen af input.

Tidsompleksiteten for en grafisomorfialgoritme er et udtryk for, hvordan antallet af skridt, som algoritmen i værste fald skal bruge, afhænger af grafens størrelse. Man kan let lave sin egen algoritme, som starter fra en ende af – vælg en knude i graf 1 og match den til en knude i graf 2. Vælg så en ny knude i graf 1 og match til en, som ikke er matchet endnu i graf 2. Og så fremdeles. Hvis graferne begge to har n knuder, er der n knuder i graf 2 at vælge imellem, når den første skal matches, n-1, når den næste skal matches etc. Så der er nx(n-1)x(n-2)x….2×1 =n! mulige match af knuderne i den en med knuder i den anden. Så skal man for hvert match af knuder checke, om kanterne passer. Er der en, der passer, er svaret “ja, der findes en isomorfi.” Ellers er svaret “Nej”. Det er ikke effektivt. Når man går fra at have 100 knuder til 1000 knuder, er antallet af mulige match for 100 knuder 100!, som er cirka 10^157 (157 nuller efter 1-tallet). Har man 1000, er der 1000! cirka 10^2567, altså 2567 nuller efter 1-tallet. Dette er en algoritme med en helt urimelig  tidskompleksitet. Blot ved at få en graf, der har 10 gange så mange knuder, skal algoritmen bruge 10^2410 gange så lang tid. Men det er også en meget ubegavet algoritme.

Har man små datamængder, kan man nøjes med sådanne dumme algoritmer, der prøver alle muligheder  (de kaldes også brute force algoritmer) og leve højt på, at computere er hurtige. Men vi har store, meget store, datamængder. så vi skal være dygtigere.

Kompleksiteten af en algoritme er det antal operationer, der skal til, som funktion af størrelsen af input. En graf består af en mængde knuder og kanter, så her er størrelsen af input den samlede størrelse af disse to mængder. Mere præcist er det “størrelsesordenen” af antallet af operationer. Hvis antal operationer er er kompleksiteten O() og man er ikke interesseret i konstanten 32 eller leddene med lavere grad.

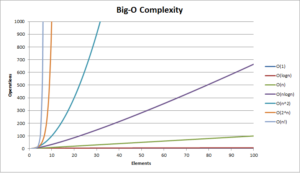Man inddeler beslutningsproblemer, altså ja/nej problemer, som eksempelvis, om der findes en matching af to grafer, efter kompleksitetsklasser – polynomiel, logaritmisk, eksponentiel etc.. Altså efter, hvad tidskompleksiteten er af den bedste algoritme. At finde en optimal algoritme er selvsagt mindst lige så vanskeligt som at afgøre, hvad kompleksiteten af en sådan algoritme ville være, hvis man kunne finde den.

Graferne på billedet illustrerer, hvordan klasser af funktioner vokser i forhold til hinanden. Læg mærke til, at n! er den, der vokser hurtigst. Den orange er , altså eksponentiel ( Grafisomorfiproblemet beskriver sin egen kompleksitetsklasse GI, som er alle problemer, man ved har samme kompleksitet som grafisomorfiproblemet – fordi man kan formulere det at løse det ene beslutningsproblem som et spørgsmål indenfor løsning af det andet problem og omvendt. Grafisomorfialgoritmerne har man hidtil haft i en klasse for sig, hvor man ikke har vidst, hvor de hører til. Det åbne spørgsmål er, om der findes en algoritme med polynomiel tidskompleksitet, der altid korrekt kan fortælle, om to grafer er isomorfe.  Altså en algoritme, hvis tidskompleksitet er et polynomium. Og det må gerne være et 2000-grads polynomium. Men man har ikke været i nærheden af at have en sådan algoritme. Man vidste, man kunne lave en, der er højst , hvor n er antal knuder. Den kompleksitet kaldes subeksponentiel – ikke polynomiel, men heller ikke så voldsom, at den er eksponentiel. Den algoritme er fra 1983, så det er derfor, der er røre i andedammen, når der kommer nyt.

Laszlo Babai har, hvis altså beviset holder, lavet en algoritme med tidskompleksitet hvor c er en konstant. Det er “quasipolynomielt” og klart mindre end det tidligere opnåede. Konstruktionen af algoritmen har involveret resultater fra det matematiske område gruppeteori.

På Numb3rsbloggen har Hans Hüttel skrevet om P versus NP. Kompleksitet af algoritmer har både teoretiske og praktiske sider. Eksempelvis har jeg lige hørt i kaffestuen, at digitalt tv ikke ville fungere, hvis vi brugte den dumme signalbehandlingsalgoritme, som er . Heldigvis bruger vi Fast Fourier Transform, som er , og så er der Vild med Dans på skærmen.

Nu er det spændende, om Babai er på vej mod en polynomiel algoritme. Grafisomorfi har også praktiske anvendelser – og der er såmænd gode algoritmer til at bestemme om visse typer af grafer er isomorfe. Helt generelt gælder det, at man med mere viden om det data, der skal behandles, kan lave hurtigere algoritmer.

Jeg har bedt min gode kollega Hans Hüttel om hjælp til at undgå alt for meget vrøvl i ovenstående – jeg er nemlig overhovedet slet ikke ekspert i kompleksitet, og han har reddet mange af mine misforståelser – der er muligvis nogen tilbage. Det er ikke Hans’ skyld. Hans skriver yderligere:  Noget andet, der er rigtig interessant, er om grafisomorfi-problemet mon også er i coNP, dvs. om problemet om to grafer _ikke_ er isomorfe mon er i NP. Ingen ved nemlig om NP er lukket under komplement (selv om der hvert år er studerende på 5. semester på datalogi, der mener at vide at det er tilfældet). Hvis vi finder en polynomiel afgører for grafisomorfi har vi samtidig fået aflivet en kandidat til at vise at NP ikke er lukket under komplement.