Der er mange andre aspekter af matricer, vektorer, produkt af matricer etc. end det, der ligger først for, nemlig løsning af lineære ligningssystemer. I et tidligere blogindlæg så vi på en ret lavtflyvende anvendelse, nemlig ideen om, at tal stillet op i et rektangulært skema, kan repræsentere billeder. Der kom lineær algebra ikke alvorligt i spil. Her tager vi, igen med udgangspunkt i bogen When Life is Linear: From Computer Science to Bracketology,  fat i matrix-vektorprodukt, egenvektorer og hvad det mon har med grafer at gøre. (Og hvad en graf er…).

Her er igen en matrix og en vektor .

Man kan gange en matrix med en vektor og få en ny vektor. En matrix med m rækker og n søjler kan ganges med en vektor med n koordinater og giver så en vektor med m koordinater. Matricen og vektoren ovenfor kan altså ganges sammen. Resultatet er en vektor med 3 koordinater. Det giver en funktion, som tager en vektor med n koordinater ind og giver en med m koordinater ud – fra til og går som følger:

1) Tag skalarproduktet af første række i matricen med vektoren v. Det giver . Det er første koordinat i vektoren . Og nej, det er ikke kønt, man man kan se, hvad der ganges med hvad.

2) Anden koordinat fås ved skalarprodukt af anden række i A med v etc.

Hvis matricen B er kvadratisk, altså har lige mange søjler og rækker, så har produktet Bw lige så mange koordinater som w.

Her er en kvadratisk matrix   Den er endda symmetrisk – hvis man spejler den i den diagonal, der går fra nordvest til sydøst, får man samme matrix tilbage. Det er nabomatricen for grafen 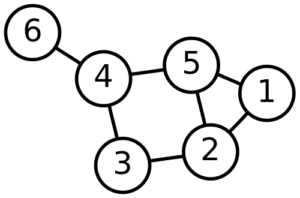 her. I den første række står 1 i søjle 2 og 5, fordi knude nummer 1 er forbundet til knuderne 2 og 5. Og så fremdeles. Bliver man mon klogere af at opstille nabomatricen? Ja, det gør man. Ganger man B med sig selv (se mine Pencasts, 1 og 2 om hvordan man gør det.) får man matricen , som indeholder information om, hvor mange stier af længde to, der er mellem knuderne. Eksempelvis er indgangen i 2.række, fjerde søjle skalarprodukt af anden række i B, som er (1,0,1,0,1,0),  med fjerde søjle i B, som er (0,0,1,0,1,1). Det tæller sammen, hvor mange steder 1-tallerne matcher. Det gør de på 3. og 5. koordinat. Så der er en sti fra knude 2 til knude 4 via knude 3 og en via knude 5.  Den første række (og første søjle) fortæller, hvor mange stier af længde 2, der er fra knude 1. Der er 2 stier fra 1 tilbage til 1, nemlig 1 til 5 til 1 og 1 til 2 til 1. Der er en sti til knuden 2, nemlig 1 til 5 til 2. og tilsvarende for knuderne 3, 4 og 5. Man kan ikke komme til 6 i to skridt, så der står 0. Nu kan læseren nok forudse, hvad der sker, hvis vi udregner etc. Men det gør jeg ikke her.

Der er andre matricer hørende til en graf: Et eksempel er Laplacematricen:  I diagonalen står antal af kanter, der udgår fra den tilsvarende knude, så der står 2,3,2,3,3,1, fordi eksempelvis knude 5 er forbundet til 3 andre, mens nummer 6 kun er forbundet til en anden. Udenfor diagonalen står , indgangene i B med negativt fortegn.

Summerer man elementerne i en given række eller søjle, får man 0 (tænk over det – det er ikke svært). Så matrix-vektorproduktet , hvor v=(1,1,1,1,1,1),  giver 0-vektoren.

Vektoren v er altså en egenvektor for matricen L(B) med tilhørende egenværdi 0. For en kvadratisk matrix A er w en egenvektor med tilhørende egenværdi s, hvis Aw=sw og hvis w ikke er 0-vektoren (det ville være snyd…). Altså hvis effekten af at gange w med A blot er at strække eller skrumpe vektoren w med faktoren s.

Vi har set, at L(B) har 0 som egenværdi med vektoren (1,1,1,1,1,1) som tilhørende egenvektor. Det siger ikke noget om grafen, for det er altid sådan for Laplacematricen hørende til en graf. Alle vektorer (k,k,k,k,k,k,k) er egenvektorer hørende til egenværdien 0. Men der er information at hente i de “næste” egenværdier/egenvektorer:

1. Alle egenværdierne er ikke-negative.
2. Egenværdien 0 har geometrisk multiplicitet 2 (der er andre egenvektorer end blot (k,k,k,k,k,k,k)) hvis og kun hvis grafen ikke er sammenhængende. Det er ret let at se, at det gælder den ene vej: Hvis grafen ikke er sammenhængende kan man omnummerere hjørnerne, så de første udgør en sammenhængende del og de sidste en anden. Laplacematricen bliver da blokdiagonal: Med seks hjørner, hvor de fire første hænger sammen og de sidste to hænger sammen får man og vektoren (1,1,1,1,-1,-1) er en egenvektor hørende til egenværdien 0 (fordi begge hjørnematricer er Laplacematricer.) Hvis der er k sammenhængskomponenter, er der k lineært uafhængige egenvektorer hørende til egenværdien 0.
3. Der er også information i egenvektoren/egenvektorerne hørende til den næstmindste egenværdi: Den kaldes Fiedlervektoren og siger, sammen med størrelsen af den næstmindste egenværdi noget om “hvor godt” dele af matricen hænger sammen. Fjerner man nogle kanter, bliver den næstmindste egenværdi mindre. I eksemplet får vi egenvektoren <0.415, 0.309, 0.069, −0.221, 0.221, −0.794> og egenværdi 0,723 (afrundet). Der er fire positive koordinater, nummer 1,2,3,5 og to negative, 4 og 6. De tilsvarende knuder i grafen hører sammen – 6 sidder ude for sig selv og kun fast i 4. Og de to dele er sammenhængende. For en fuldstændig graf, hvor alle knuder er forbundet med alle andre, har Laplacematricen to egenværdier, nemlig 0 og antal knuder, n. Så den næstmindste er antallet af knuder. Den har n-1 lineært uafhængige egenvektorer af typen (-1,0,0,…,1,0,…,0) Altså -1 i første koordinaten, 0 alle andre steder undtage et sted, hvor der står 1. Den næstmindste egenværdi er altså højst n og i så fald er grafen så sammenhængende, som den kan blive.

Spektral grafteori drejer sig om egenværdier og egenvektorer for matricer, der hører sammen med grafer, såsom nabomatricen og Laplacematricen. Der er forbindelser til netværk af elektriske modstande, til tilnærmelser af funktioner,… Se for eksempel Daniel A Spielmans  noter. Det er meget smukt og smart. Og som tidligere gælder det om at forstå graferne og matricerne på flere måder: Hvad er den lineære funktion svarende til nabomatricen? Hvordan kan man “se” den på grafen? Hvad med Laplacematricen?  Fun fact: For en vektor v=(v1,v2,…,vn) og en Laplacematrix for en graf, er summen af alle de differenser , hvor det i’te og j’te hjørne er forbundet med en kant. I eksemplet ovenfor, ville man få . For en fuldstændig graf får man alle

Grafer bruges som modeller mange steder, og der er en stor interesse i eksempelvis algoritmer, der finder længste/korteste vej, centralitet (hvilke knuder er centrale, så man skal igennem dem næsten uanset, hvor man kommer fra og til) og meget mere. Der er netværk af Facebookvenner, af www-sider, af neuroner i hjernen, af byer via veje, via flyruter, via jernbane,…