Mandag 18.april 13-15 kommer Steffen Lauritzen heldigvis til Aalborg.

Steffen Lauritzen

Denne gang for at holde tiltrædelsesforelæsning som adjungeret professor. OG der er reception bagefter.

Tilmelding senest 11.april til merete@math.aau.dk, så der er mad nok til receptionen… Flere oplysninger og det officielle opslag finder I her

Titlen og Resume:  Challenges in Graphical Models

Resume: ”Grafiske modeller har nu eksisteret i næsten fyrre år og har i den periode spillet en hovedrolle i mit videnskabelige liv. I forelæsningen skal jeg forsøge at give eksempler på hvad de er, hvordan de kan anvendes, og hvorfor de er interessante. Jeg vil også identificere vigtige historiske milepæle og forsøge at give indtryk af den seneste udvikling og nuværende udfordringer i forbindelse med deres teori og anvendelse – udfordringer, som jeg håber at tage op i den nærmeste fremtid.”

Det skal I komme og høre. Steffen er en fremragende forelæser og en af de helt store i statistik.

Grafiske Modeller dækker i sandsynlighedsteori og statistik over modeller, hvor afhængigheden er beskrevet ved en graf.

Bayesiansk Net.

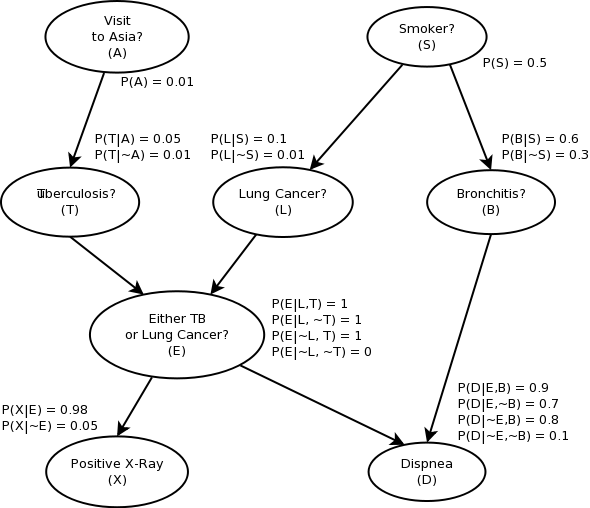
Her er et Bayesiansk netværk, som er et eksempel på en grafisk model. Øverst til højre er knuden “Ryger”. Der er, ifølge grafen, sandsynlighed 0,5 for, at man ryger. Er man ryger er der en vis sandsynlighed for, at man har lungekræft P(L|S)=0,1  og en anden for at have bronkitis P(B|S)=0.6. Sandsynligheden for at have lungekræft, hvis man ikke ryger, er P(L|~S)=0,01, så “tilden” ~betyder “ikke” eller “non”.  Til venstre for oven er en knude for at have været i Asien – det har 1% af befolkningen, P(A)=0,01, og sandsynligheder for, at man i så fald har tuberkulose hhv. lungekræft. De nederste knuder er hhv. at have et bestemt røntgenbillede (positivt…) og at have Dyspnoea, som  er kortåndethed. Bayes’ formel

giver en sammenhæng mellem betingede sandsynliheder den ene og den anden vej, så man kan spørge, hvad sandsynligheden er for, at en tilfældig person, som har lungekræft er ryger, P(S|L), kan udregnes, hvis man kender P(L|S) og det gør vi, P(S) kender vi også her, men vi kender ikke P(L), altså sandsynligheden for, at en tilfældig person har lungekræft.

Udfra netværket ovenfor, kan man eksempelvis regne på, hvad sandsynligheden er for, at en person, der har positivt røntgenresultat, kortåndethed og har været i Asien, har lungekræft. Man indtaster disse oplysninger og kan så opdatere sandsynlighederne i netværket – belief-propagation – ved som udgangspunkt at bruge Bayes’ formel.

Det er jo fint nok, men bliver netværkene store, kan det være beregningsmæssigt meget voldsomt, da der som udgangspunkt er sammenhæng op og ned og på tværs af hele nettet. Lauritzen Spiegelhalter algoritmen giver en effektiv måde at gøre det på – man kan lave visse udregninger færdige i en lille del af netværket og så føde dem ind i den større sammenhæng. Det udnyttes f.eks. i programmerne fra Hugin, som er startet af bl.a. Steffen Lauritzen. Man kan hente en demo, Hugin Light, som man kan lege med, hvis ens netværk ikke er for store. Sådanne netværk kan bruges til beslutningsstøtte.

Men kom til foredraget. Steffen fortæller det meget bedre.