Keplerproblemet er løst i dimension 8 og 24.

I marts offentliggjorde den ukrainske matematiker Marina Viaszovska , som lige nu er på Humboldt Universitetet Berlin, en artikel, som giver løsningen på kuglepakningsproblemet i dimension 8, og en uge efter kom en opfølger, hvor hun sammen med andre havde løsningen på problemet i dimension 24.

Spørgsmålet er simpelt nok: Hvor stor en andel af planen, rummet, det 4-dimensionale rum,,,, kan man fylde ud ved at pakke kugler med samme radius så tæt som muligt. En kugle i det n-dimensionale rum, er de punkter/vektorer $(x_1,\ldots , x_n)$ , som har (Euklidisk) længde højst 1: $x_1^2+\ldots + x_n^2 \leq 1$

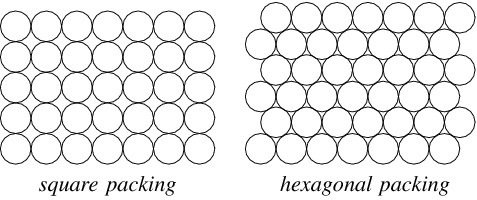
$To cirkelpakninger. Den til højre er tættere end den til venstre. (Fra MathWorld.)$

To cirkelpakninger. Den til højre er tættere end den til venstre. (Fra MathWorld.)

Allerede i 1892 vidste den norske matematiker Axel Thue, at den mest effektive måde at pakke cirkler i planen ville fylde $\pi/2\sqrt{3}$ ca. 91% af arealet ud. For eksempel ved et heksagonalt mønster, som i en bikube. Hans bevis (som kom i 1910) var ikke korrekt, så det første bevis er fra 1940 og skyldes Fejes Toth.

$Kuglerne pakkes med hvert lag efter den plane hexagonale pakning. Så stables lagene efter forskellige regler. Der er flere, der giver en optimal pakning i dimension 3.$

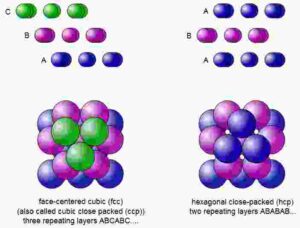
Kuglerne pakkes med hvert lag efter den plane hexagonale pakning. Så stables lagene efter forskellige regler. Der er flere, der giver en optimal pakning i dimension 3.

I dimension 3 fylder den tætteste pakning $\pi/(3\sqrt{2})$ ca. 74% og er for eksempel den, man får ved at pakke efter hjørnepunkter og center i kuber. Det var forbavsende vanskeligt at vise. Gauss viste allerede i 1831, at den pakning er den tætteste blandt gitter/lattice-pakningerne. Men der kunne jo være andre typer pakninger, som var bedre. I 1998 viste Thomas Hales, at det faktisk er den tætteste pakning – beviset var meget langt og brugte computere, så det var omdiskuteret, om det faktisk var korrekt,

$Lagene pakkes sammen. Med forskellig forskydning.$

Lagene pakkes sammen. Med forskellig forskydning.

men det mener vi nu, at det er.

En pakning beskrives ved koordinaterne for centrum af kuglerne, altså en (uendelig) delmængde $\Lambda$ af vektorer i $R^n$ . Det kaldes en gitterpakning, hvis

Hvis x og y er i $\Lambda$ , så er x+y og x-y også i $\Lambda$ . (Så 0 er altid med – tænk over det.)
Hvis x er i $\Lambda$ , så er x isoleret: Der findes et (muligvis lille) d>0, så der ikke er andre gitterpunkter i kuglen med centrum i x og radius d.
$\Lambda$ “fylder noget” – det er ikke indeholdt i noget n-1 dimensionalt underrum af $R^n$ . Eksempelvis må et gitter i planen ikke holde sig indenfor en linje. I rummet må det ikke ligge i en plan. etc.

Eksempelvis er mængden af punkter med heltallige koordinater et gitter. I planen er centrene givet som alle heltallige linearkombinationer – hvad man kan få ved at lægge vektorer sammen, gange dem med hele tal og kombinere disse – af vektorerne $\{ (2,0), (1, \sqrt{3})\}$ I dimension 3 er det (for eksempel) kombinationer af $\{ (2, 0, 0),(1, 1, 0),(0, 1, 1)\}$

I dimension 8 og 24 er der gitre, som giver en meget tæt pakning. E8-gitteret og Leech gitteret. Tætheden af E8 er $\pi^4/(2^4 4!)$ ca. 25% og tætheden af Leech gitterpakningen er $\pi^{12}/12!$ ca. 0,19% De nye resultater er, at de to gitre faktisk giver den tætteste pakning. Specielt er den tætteste pakning altså en gitterpakning. Både E8 og Leech-gitteret har forbindelser til mange områder af matematik (Leech lattice har bl.a. forbindelse til Golay-koder, men det får I ikke mere om her)- og beviset har krævet konstruktion af nye funktioner, som er i familie med det, der er kernen i beviset for Fermats sætning, nemlig modulære former!

Problemet er altså løst i dimensionerne 1,2,3,8 og 24. Generelt har vi en nedre grænse for, hvor tæt, en pakning nødvendigvis må være, hvis der ikke er huller, som er store nok til at proppe endnu en kugle ind: Hvis vi har lavet en pakning, hvor der ikke er plads til en kugle mere, så er der ingen punkter, som har afstand mere end 2r til alle kugler (r er radius af kuglerne). Så hvis vi tog kugler med dobbelt så stor radius og anbragte i samme centre, så ville hele rummet R^n være dækket. Dobbelt radius giver $2^n$ gange så stort volumen. Altså havde vi dækket mindst $1/2^n$ med den oprindelige pakning. Bemærk, at der ikke er nogen opskrift med til at placere kuglerne. Det er et ikke-konstruktivt bevis.

Hvorfor mon den andel, der bliver dækket, aftager med voksende dimension? Det kan man måske forstå, når man ser på volumen af n-dimensionale kugleflader. Formlerne er som følger for en kugle med radius R:

$V_{2k}(R) = \frac{\pi^k}{k!}R^{2k},$ for lige dimensioner 2k

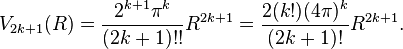$V_{2k+1}(R) = \frac{2^{k+1}\pi^k}{(2k+1)!!}R^{2k+1} = \frac{2(k!)(4\pi)^k}{(2k+1)!}R^{2k+1}.$ for ulige dimension 2k+1. Volumen går mod 0, hvis radius holdes fast mens dimensionen vokser. Derimod er volumen af en kasse med sidelængde 2R (som kuglen kan puttes ned i) $(2R)^n$ . Hvis man pakker efter systemerne, man fandt i lavere dimensioner – det kan man give en slags mening til – så bliver der mindre og mindre fyldt ud.

E8 kan ses som 1) Lav den pakning, der svarer til den hexagonale kubiske i dimension 3 – udfra vektorerne, jeg gav ovenfor – passende udvidet og lagt ind i dimension 8. Så bliver der huller med plads til flere kugler – systematisk. Fyld dem ud. Det giver E8. I E8 er kyssetallet – de kugler der rører en givet kugle – 240. I Leech-gitteret, som kan konstrueres udfra E8, men også på mange andre måder, kysses der meget – kyssetallet er 196560.