Som matematiker er jeg, ligesom Buzz Lightyear, vant til at tale om og at omgås uendelig – 1/x går mod 0, når x går mod uendelig – og lignende udsagn giver mening for mig. Det gør det, fordi jeg ved, der er præcise definitioner bag. Denne blogpost skal handle om at lægge tal sammen, rigtig mange tal. I en vis forstand at lægge uendelig mange sammen.
Summen kommer tættere og tættere på
jo flere led, der tages med. Mere præcist, så er det sådan, at uanset hvor lille et tal
, min værste fjende vælger, så vil jeg kunne finde et (måske meget stort) tal N, så
ligger mellem
og
og det gør
også, når
.
Og det er det, vi mener med, at en sum “går mod” og faktisk at den uendelige sum “er lig med” et tal, så vi skriver
At det rent faktisk er , er et klassisk problem, Baselproblemet, som
 Leonhard Euler (se billedet) gav det første bevis for. Man kan bruge resultatet til at approksimere
Leonhard Euler (se billedet) gav det første bevis for. Man kan bruge resultatet til at approksimere – ved at lægge flere og flere tal sammen i denne sum – det går nu ret langsomt i forhold til andre metoder, som også bygger på, at noget “går mod” noget med $latex\pi$.
Andre eksempler er
, den naturlige logaritme til 2. Bemærk, at nogle led bliver lagt til, andre trukket fra, så efterhånden som flere led lægges til, skyder man skiftevis over og under
, men mindre og mindre over og under.
En uendelig sum kaldes en række (series på engelsk, hvis I vil Google) og summen op til et vist kaldes en afsnitssum. En række er altså ikke selv en sum, men en opskrift på afsnitssummer.
, grundtallet for den naturlige logaritme.
Der er mange forskellige metoder til at afgøre, om sådan en sum konvergerer og i så fald mod hvad. En uendelig sum er konvergent, hvis der findes et tal, den “går mod”, når flere og flere led lægges til, sådan som ovenfor. er den ikke konvergent, så er den divergent. Sommetider er det meget let at afgøre, at summen divergerer. For at rækken skal konvergere, må de led, man lægger til, blive mindre og mindre. Gør de ikke det, er den i hvert fald ikke konvergent. Et klassisk eksempel på en divergent række, er den harmoniske række:
Der er flere forskellige argumenter for, at den divergerer: Et går via sammenligning med et integrale:
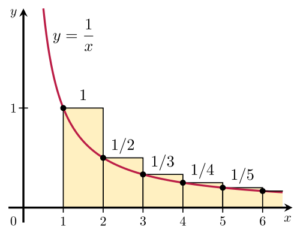
Figuren viser grafen for funktionen 1/x. Den illustrerer, at arealet under denne kurve, fra 1 til uendelig, er mindre end summen af den harmoniske række. Og dette integrale får man ved at lade M gå mod uendelig i . Det går mod uendelig. Så den harmoniske række er divergent. Men det går langsomt mod uendelig. Meget, meget langsomt.
I går lærte jeg, ved at læse min gode kollega Kevin Knudsons indlæg i Forbes, følgende svimlende faktum:
Hvis vi var begyndt ved Big Bang med at lægge tallene i den harmoniske række sammen og havde lagt et til hvert sekund, så var vi nu nået til et sted mellem 40,6 og 41,6. Udregningen går på, at Big Bang var for 13,8 milliarder år siden , år. Et år har 31 556 926 sekunder, ca.
(nogen siger
for at huske det). Det er altså
sekunder. Tag den naturlige logaritme (
og se, at Kevin har ret – Intervallet, Kevin har med, er en kombination af, at tidspunktet for Big Bang ikke er helt klart, og at den harmoniske række er større end det integrale, vi her regner på.