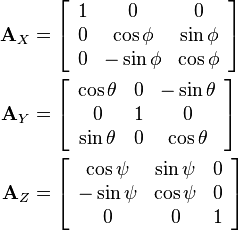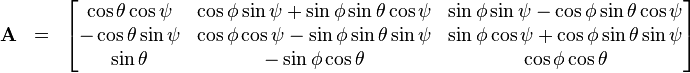Der er kvaternioner i computerspil, i flysimulatorer og i styring af robotter, der skal rotere. Hvad mon de laver der?

Kvaternionerne blev opdaget af den irske matematiker og fysiker, W.R. Hamilton. Han fik den fundamentale indsigt om dem, da han spadserede langs Royal Canal i Dublin og der sidder nu en

mindeplade på den bro, Broome Bridge hvor han efter sigende skriblede ligningerne

, , ,  .

Kvaternioner er tal, på formen a+bi+cj+dk, hvor a, b, c, d er reelle tal og i,j,k er symboler, som  kan lægges sammen som vektorer med 4 koordinaterog ganges sammen efter reglerne ovenfor. altså samme system som med de komplekse tal, men der er nu kommet j og k med. Eksempel:

og hvor jeg brugte reglerne ovenfor, da jeg gangede i,j og k med hinanden. Bemærk, at og tilsvarende for de andre produkter, der ikke er nævnt ovenfor.  i,j og k antikommuterer.

Kvaternionerne er en divisionsalgebra eller et skævlegeme. I får ikke regnereglerne for divisionsalgebraernes addition og multiplikation, men jeg har brugt mange af dem ovenfor. De reelle tal og de komplekse tal er også divisionsalgebraer (med kommutativ multiplikation). Tager man udgangspunkt i addition af vektorer og forsøger at finde en multiplikation, der “matcher”, kan man kun gøre det for for har man en multiplikation, der giver  Cayleytallene, men der er multiplikation ikke associativ: (ab)c er ikke nødvendigvis a(bc).

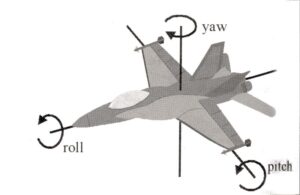
Hvad har det med computerspil og jagerfly at gøre?

En rotation i det 3-dimensionale rum kan beskrives ved en rotationsakse og en vinkel. Har man valgt sig et koordinatsystem, kan alle rotationer beskrives som en kombination af rotation om x-aksen, derefter om y-aksen og derefter om z-aksen. Man kan altså beskrive det ved de tre vinkler.

For jagerpiloter hedder det “roll”, pitch” og “yaw”, når man roterer om flyets egne interne akser. Man kan lege med Roll Pitch og yaw her (klik på Euler angles i øverste højre hjørne). Det er naturligvis ikke det samme som at vælge nogle faste akser, som ikke følger med flyet, men der er omregninger frem og tilbage mellem diverse systemer af vinkler og akser. Man er i øvrigt (heller) ikke enige om, hvilken akse, der roteres om først, så man skal være vågen, hvis man henter formler flere steder fra. Orienteringen  af et objekt i  rummet kan altså beskrives med tre vinkler, som siger, hvordan objektet er roteret i forhold til nogle faste x,y,z akser.De kaldes også Eulervinkler. Samme position kan svare til flere forskellige vinkler – hvis vi måler i radianer, gentager de sig for hver ;  i grader er perioden 360. Bemærk, at det drejer sig om orienteringen af et 3-dimensional objekt, ikke bare den retning, eksempelvis næsen på flyet peger i.

Så den rotation, der er lavet for at bringe flyet i en bestemt position, kan beskrives med tre vinkler, altså et punkt (u,v,w) i . Og man skal ikke bruge mere end de vinkler, der er i kassen, som er afgrænset af

, ,

for at være sikker på, man har alle rotationer med. Kunne man mon nøjes med færre vinkler – giver nogle vinkler de samme rotationer? (Svar: Ja) Hvordan er kassen “limet sammen”? Hvordan svarer punkter i den ene ende til dem i den anden, top til bund og front til bagside? Hvordan ser det ud, når et fly ændrer sin position og går via “ydervinklerne”. M.a.o. hvordan ser det ud i vinkler, når et fly laver loop, barrel roll og andre luftakrobatiske manøvrer? Hvordan laver man en kontinuert rotation, der bringer flyet til en bestemt position i rummet, altså en kontinuert kurve i mængden af rotationer. Det er der, det bliver interessant. Og hvor beskrivelsen med Eulervinkler må give op.

Matrixbeskrivelse.

En rotation kan beskrivesmed en 3×3 matrix, hvis første søjle er koordinaterne for vektoren [1,0,0] efter rotation, anden søjle er koordinaterne for [0,1,0] efter rotation og tredje søjle er koordinaterne for [0,0,1] efter rotation. Som udgangspunkt er der 9 tal i en 3×3 matrix, men en rotations matrix skal opfylde en stribe ligninger, som kommer udfra at søjlerne har længde 1, står vinkelret på hinanden og udgør et højrehåndssystem. (Da de jo er resultatet af at rotere basisvektorerne). Rotationsmatricerne udgør delmængden SO(3) af 3×3 matricerne. Det er en 3-dimensional delmængde af det 9-dimensionale rum, som svarer til de 9 tal i en 3×3-matrix. Enhver rotationsmatrix kan skrives som et

produkt af matricer, der svarer til rotation om x,y,z akserne. Altså udfra tre vinkler.

 

 

 

 

Med vinklen bliver den samlede rotation

Jeg har brugt additionsformler for sinus og cosinus. Bemærk, at rotationen ikke afhænger af og hver for sig, men kun af deres sum. Altså at eksempelvis giver samme rotationsmatrix uanset hvad er hver for sig. Det betyder, at beskrivelsen med vinkler er fejlagtig. Det ser ud somom, der kun er to “retninger” at vælge imellem, når man skal rotere væk fra positioner med , men der skal være 3.

Dimensionen af mængden af rotationer er 3. Det er et ægte praktisk problem, som får robotter til at gøre pludselige skift på 180 grader eller (mindre alvorligt) computerspil til at se mystiske ud, når jagerfly kommer i position med eksempelvis næsen opad. (Den ubestemthed, der er i situationen, hvor man ikke kan se, hvad de to vinkler er, kan have sære effekter.) Så der er en god grund til at gøre noget ved det.

Man kan tænke på en lidt analog situation, hvor man nærmer sig Nordpolen langs en meridian, altså med fast længdegrad. man har altså breddegrad, der vokser mod . Kigger man i systemet af længdegrader og breddegrader, vil man ikke kunne se, at en kurve op til Nordpolen langs Greenwichmeridianen (længdegrad =0) og væk fra Nordpolen langs en meridian med vinkel , slår et knæk på Nordpolen. Eller at kurven, der går op langs Greenwichmeridianen og væk langs datolinjen faktisk ikke knækker. Det skyldes, at systemet med længde- og breddegrader klemmes sammen i Nordpolen, så breddevinkel og længdegrad hvadsomhelst, er samme punkt, nemlig Nordpolen.

Kvaternionerne er bedre: 

Kvaternioner med længde 1 beskriver rotationer. Til en sådan kvaternion q=w+xi+yj+zk svarer rotationsmatricen

Som man kan se, giver kvaternionen -q samme rotation, men det er den eneste “sammenlimning”, der sker, når man afbilder fra enhedskvaternionerne til rotationerne. Enhedskvaternionerne udgør en 3-dimensional kugleflade – det er jo vektorer med 4 koordinater af længde 1. Effekten af at bruge kvaternioner til at beskrive rotationer er, at man har den rigtige dimension og i analogi med eksemplet med Nordpolen, nu kan se forskel på, om kurver af rotationer knækker eller ej, men der er andre gevinster: Skal man beskrive en kurve af rotationer, altså rotere fra en position til en anden gennem mellempositioner, så er det meget let at gøre med kvaternioner – man laver en kurve r(t) i , som starter i q1 og ender i q2 og ikke passerer 0. Nu skal man sikre sig, den holder sig indenfor kvaternioner med længde 1, men det er let. Man bruger bare r(t)/|r(t)|, altså dividerer med længden hele vejen. Skulle man gøre det med rotationsmatricer, var det ikke så let – en matrix, der ikke er en rotationsmatrix kan ikke med et snuptag korrigeres ind til rotationsmatricerne.