I dag er det Einsteins fødselsdag, hurra, hurra, hurra. (Og det er Pi-dag)

Nå, blogge eller ikke blogge om $\pi$ -dag? Det er jo hamrende uinteressant, at datoen idag har noget at gøre med de første decimaler af $\pi$ . Hvis du har undgået at løbe ind i begrundelsen for at holde $\pi$ -dag, så er den her: I USA skriver man datoer med måneden først, så 14.marts bliver 3/14. Og de første cifre i decimaludviklingen af $\pi$ er 3,14.

$Pi Pie fra Delft.$

Pi Pie fra Delft.

Jeps, det er en søgt undskyldning for at spise pie og tale om $\pi$ , men lad os nu hoppe på den. Og ellers så fejrer vi bare Einstein.

$\pi$ er forholdet mellem omkreds og diameter i en cirkel. Ikke bare en enkelt cirkel, men alle cirkler har det samme forhold.

$\pi$ er irrationelt og ovenikøbet transcendent:

De rationale tal $\mathbb{Q}$ er de tal, der kan skrives som en brøk p/q mellem hele tal. De irrationale tal er de reelle tal, der ikke kan skrive som en sådan brøk. At $\sqrt{2}$ er irrationalt ved mange fra gymnasiet og matematikerne har vidst det i mere end 2000 år. I 1761 viste J.H. Lambert, at $\pi$ er irrationalt.
Tal, der er rødder i polynomier med heltalskoefficienter kaldes algebraiske. Eksempelvis er $\sqrt{2}$ rod i andengradspolynomiet $x^2-2$ og det komplekse tal $i$ er rod i $x^2+1$ . Alle tal er sådan set rødder i polynomier: $\pi$ er rod i polynomiet $x-\pi$ , så det vigtige er koefficienterne. Et polynomium $a_nx^n+a_{n-1}x^{n-1}+\cdots a_1 x+a_0$ , har heltalskoefficienter, hvis alle koefficienterne $a_i$ er hele tal. Tal, der ikke er rødder i et polynomium med heltalskoefficienter kaldes transcendente. At $\pi$ er transcendent viste von Lindemann i 1882.

Det er forbavsende hvor mange steder, $\pi$ dukker op. Tidligere på bloggen i Mod det uendelige univers havde vi Eulers resultat om, at $1+ \frac{1}{4} +\frac{1}{9} +\frac{1}{16}+\cdots+\frac{1}{n^2}+\cdots = \frac{\pi^2}{6}$ . Så der kommer $\pi$ nok lidt overraskende ind.

Periodiske fænomener får ofte bragt $\pi$ ind i billedet via sinus og cosinus. Men der er også $\pi$ i statistik.

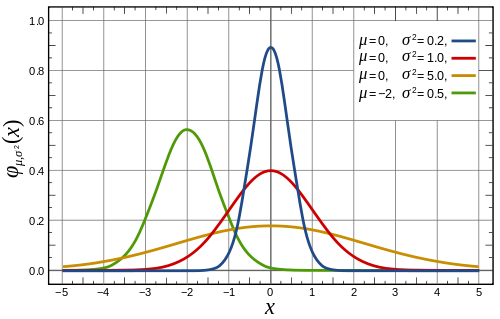
$Tæthedsfunktioner for normalfordelingen med forskellig middelværdi go spredning.$

Tæthedsfunktioner for normalfordelingen med forskellig middelværdi oo spredning.

Normalfordelingens tæthedsfunktion indeholder nemlig $\pi$ : Tæthedsfunktionen for normalfordelingen med middelværdi $\mu$ og spredning $\sigma$ har udtrykket $\varphi(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}$ . Man kan finde sandsynligheden for, at en stokastisk variabel, som er normalfordelt med disse parametre, ligger i intervallet mellem a og b, ved at udregne $\int_a^b\varphi(x) dx$ . Det må I få mere om i et andet blogindlæg eller læse her, hvor Ege Rubak forklarer, hvorfor normalfordelingen er så vigtig.

Det er ikke en tvangstanke hos matematikere, at der skal puttes $\pi$ i alting. Det kommer ud af krav til modeller, af svingninger og sommetider virkelig overraskende, hvor man skal gruble over, hvad grunden er.