Happy Ending problemet er ikke løst, men to matematikere, Ester Klein og George Szekeres, der arbejdede med det, blev gift. Så derfor kaldte Erdös det “Happy Ending-problemet”.
Det er et af de matematiske spørgsmål, som er let at forstå, men svært at løse – tilsyneladende, eftersom det ikke er løst endnu. Og det er et af dem, der er omtalt i Popular Mechanics – ligesom Collatzformodningen, Sofaproblemet og Eulermursten, som allerede er behandlet her på bloggen.
Spørgsmålet er: Tegn punkter i planen. Der må ikke ligge tre eller flere på linje. Hvor mange skal der være for at man er sikker på at kunne tegne en konveks n-kant, hvis hjørnepunkter allesammen er nogen af dem, vi tegnede? (Konveks betyder, at randen buler udad, alle indre vinkler er højst 180 grader. Tegner man linjestykket mellem to punkter i figuren, så er det indeholdt i figuren.)
Illustration fra MathWorld.
Hvis n=3 er det klart: Har man tre punkter, som ikke er på linje, er de hjørner i en trekant. Og trekanter er altid konvekse.
Kald antallet af punkter, der skal bruges, g(n). Vi ved nu g(3)=3.
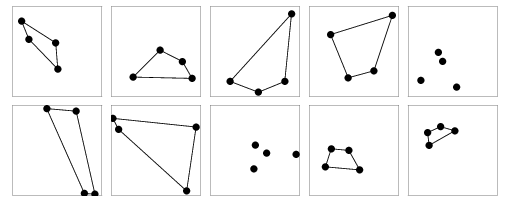
Billedet fra Eric Weissteins MathWorld illustrerer, at g(4) må være større end 4. Der er vist to tilfælde, hvor man ikke kan tegne en konveks firkant. Erdös Szekeres-formodningen siger, at 
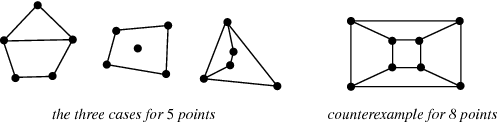
Illustrationen (igen fra MathWorld) til højre viser, at g(5)>8. Faktisk er g(5)=9. Først vist af E. Makai.
At g(6)=17 krævede computerkraft – det resultat er fra 2006.
Hvad med g(7)? Det ved vi ikke! Erdös og Szekeres viste, at g(n) er endeligt. Det overrasker muligvis ikke læseren, men hvis man ændrer problemet en anelse og spørger: Hvad er det mindste antal punkter, man skal have for at man er sikker på, der findes en konveks n-kant som ovenfor, som ikke indeholder nogen af de andre punkter (en tom konveks n-kant) så ved man, at uanset, hvor stort et N, man vælger, så kan der laves en punktmængde i planen med N punkter, som ikke indeholder nogen tom 7-kant. For en tom 6-kant gælder dette ikke, Der findes et tal, sådan at punktmængder med det antal punkter altid vil indeholde en tom 6-kant. Man ved også, at det tal er mindst 30… Se mere på Numberphile-videoen her: