Ved statsministerens pressemøde inden påske, hvor en gradvis “åbning” af Danmark blev lanceret, fortalte Kåre Mølbak fra Statens Serum Institut, at de har fremskrevet mulige scenarier ved at bruge matematiske modeller. I TV2News’ løbende undertekster stod “matematiske modeller” – altså med anførselstegn. Man kan se, at det er uvant, at der udtrykkeligt tales om matematiske modeller til et pressemøde…. selvom der er matematiske modeller bag valg af finansiering af stort set hvert eneste politiske udspil.

I Nature beder Julia Gog, britisk epidemiolog, om at slippe for, at for mange overfylder epidemiologernes inboxe og diverse preprintarkiver med halvbagte beregninger – hvis man virkelig vil hjælpe og har evnerne, vil det være godt at fortælle, hvad modellerne går ud på. Se det er et kampråb jeg kan forstå. Og reagere på.

Først lidt generelt om matematiske modeller: Det er modeller –  ikke virkeligheden. Når man laver en matematisk model vælger man at se bort fra noget af virkeligheden. Det gælder om

1. Modellen skal være simpel nok til, at man kan håndtere matematikken i den.
2. Resultaterne af at “regne” på matematiksiden skal være væsentlige og relevante for den virkelige problemstilling.
3. Output fra modellen skal kunne fortolkes, give mening og være nogenlunde retvisende for den virkelighed, der skal beskrives og påvirkes.

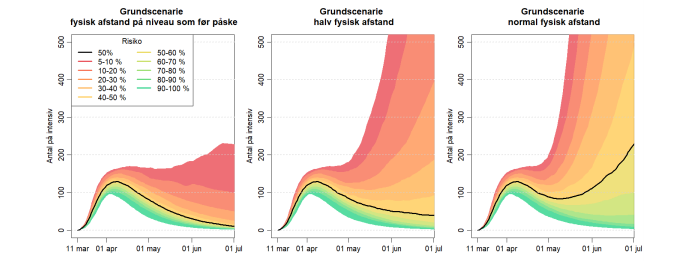
Hvor god modellen er afhænger i høj grad af, hvor godt man forstår den virkelig problemstiling, hvor meget og hvor præcist data, man har, hvor hurtigt, man kan få fat i data etc. Derfor vil output fra modeller ofte komme med flere mulige scenarier vægtet med forskellig sandsynlighed. Her er eksempelvis ekspertgruppens  prognose for indlæggelser på intensiv, hvis vi havde opretholdt restriktionerne fra før påske, men slækket på “social afstand”, som det kaldes.. Det går, som man kan se, ganske overordentlig meget galt med en ikke så lille sandsynlighed.

Hvor ved ekspertgruppen så det fra – hvordan laver de beregningerne? Hvad er modellen? Det får I ikke hele historien om – jeg er ikke epidemiolog – kan knap stave til det – men jeg kan løfte lidt af sløret – jeg har læst mig til noget og vidste lidt i forvejen.

Epidemimodeller. SIR og SEIR.

En meget simpel model for epidemier er SIR-modellen. Det er en kompartmentmodel hvor befolkningen er delt i “kasser” og flytter rundt mellem disse kasser. Her står S for Susceptible (de raske, der kan smittes), I for Infected (dem, der smitter), R for recovered (dem, der ikke smitter mere eller kan smittes). Man ser på en samlet population, som så enten er smitbare (S), smittede (I) eller (R):har været smittet, nu ikke smitbare og heller ikke smitter – herunder er også dem, der er døde.

S+I+R er konstant. Det er jo den samlede befolkning. Så Recovered inkluderer dem, der er døde.

Som tiden går flytter personer  mellem S, I og R. Det er altså funktioner af tiden S(t), I(t) og R(t).

HVordan flytter de rundt? Lad mig først udvide modellen til en SEIR, hvor E er Exposed – de er smittet, men smitter ikke endnu.

Hvor mange flytter fra S til E? Tiden kan her sættes til at svare til dage. Så hvordan udvikler S,E, R sig, hvis vi kender S(t), E(t), I(t), R(t) til et tidspunkt? Det afhænger af, hvor smittefarlig sygdommen er og hvor mange møder, der er mellem smittede og raske. Det plejer vi at modellere som en sædvanlig differentialligning (“sædvanlig” er et fagudtryk – “ordinary” er den engelske pendant –  S,E,I,R er funktioner af t, tiden og ikke andet – vi har nemlig også funktioner af flere variable):

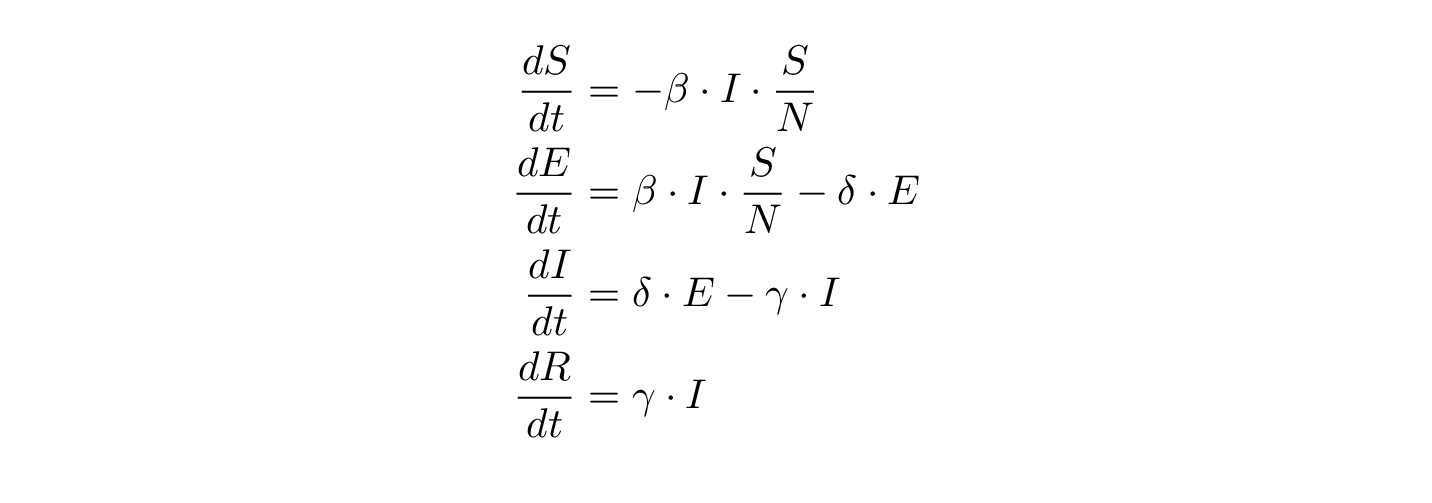
Lad mig starte nedefra:  , hvor D er det antal dage, man i gennemsnit er syg (og smitter) – det er altså den andel af de inficerede, der kommer sig og flytter til R. Den optræder (med modsat fortegn)  både i den afledte af R og den afledte af I – de flytter jo fra I til R. TIlsvarende er 1/d, hvor d er inkubationstiden – den tid, man er smittet, men ikke smitter.

er et mål for smitsomheden – den ganges med IS/N, hvor N er befolkningens størrelse – rationalet er, at man smitter, når man mødes.

Man kan allerede med denne model se, at det kan hjælpe på epidemiens udvikling at sætte syge i karantæne. Så bliver I(t) mindre  og der smittes ikke så mange.

Det er imidlertid en meget, meget simpel model. Hvis man skal lave de grafer, ekspertgruppen har lavet, skal man for eksempel vide, hvilken del at befolkningen, der bliver smittet – der er stor forskel på, hvor syg man bliver og dermed, om man skal på intensiv afdeling.

Det kan man reparere på ved at lave flere kompartments: Opdeling i aldersgrupper, som så er underopdelt i S, E, I, R, altså eksempelvis raske 0-5-årige. Det giver en finere model, hvor man kan tage hensyn til, hvilke dele af befolkningen, der mødes og dermed om de smittede 50-55-årige smitter de 0-5-årige.

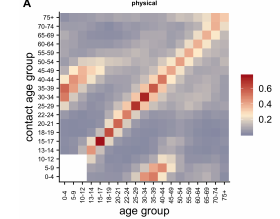
I England lavede man et “citizens science” projekt hvor 36.000 personer rapporterede om deres kontaktmønstre – hvem mødes de med og hvor (arbejde, hjemme, skole,…) Der var også automatisk indrapportering via GPS og telefoner. Ud af det kom eksempelvis kontaktmatricen nedenfor:

De hvide felter er manglende data – børn under 12 rapporterede ikke, eller der var ikke nok med.

Det giver en indikation af, at vi mødes med jævnaldrende og  børn mødes med deres forældre.

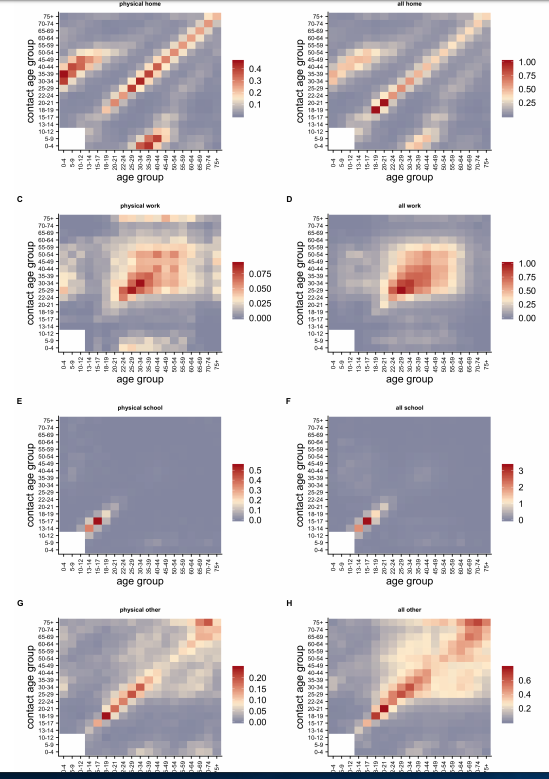
Hjælper det, at vi holder os hjemme? Det afhænger af, hvor vi mødes med hinanden og det har projektet i England også undersøgt. Søjlen til venstre er fysisk kontakt, til højre al kontakt – defineret passende – måske skal man tale med folk eller passere tæt på dem.

Det giver tydeligvis input til, hvad man får ud af at holde os hjemme fra arbejde. Desuden er fysisk kontakt minimeret ved “social distancing”. Man kan omvendt også se noget om, hvad det betyder at lade børn komme i skole.

Men, men: Det er en model for et land – Storbritannien. I Danmark er vores kontakter formentlig anderledes – i Storbritannien har de eksempelvis kostskoler, universitetsstuderende bor på universiteterne. De har færre vuggestuepladser og mange andre forskelle. Men uanset hvad: Man skal bruge viden om, hvordan og hvor vi mødes. Måske giver vi flere knus? Eller færre? (Det gør vi i hvert fald nu…)

Det er altså¨ganske indviklede modeller, men overordnet set drejer det sig om compartmentmodeller.

Den simple version, hvor befolkningen ikke underdeles efter alder, kan man læse mere om på dansk her. hvor kompartmentmodellen er udvidet med et Q for karantæne. Der er også mulighed for at “lege” med modellen. Men husk hele tiden, at det, der bruges af eksperterne, er mere kompliceret og i øvrigt skifter – man lærer mere om epidemien undervejs, kender antal syge bedre,…

Lige nu er AAU og DTU igang med en såkaldt agentbaseret model, hvor man simulerer enkeltindivider. På matematik her er det Torben Tvedebrink, Mikkel Meyer Andersen og Janus Valberg-Madsen, der er med i det projekt. Det kan være, de fortæller mere om det, men vi har jo egentlig ganske travlt med at holde universiteterne i luften med online undervisning.

Datarevolutionen er i gang og den digitale tidsalder har gjort data
mere tilgængelig end nogensinde før. Statistiske modeller og
datadrevne metoder er nødvendige for at kunne opnå viden og indsigt i de
stadigt voksende datamængder.
Det stiller krav til os alle. Begrebet “Data Science
Citizen” dækker bl.a. over evnen til at forholde sig kritisk til data
og konklusioner draget på baggrund af statistiske modeller.

I projektet “AI – Aalborg Intelligence”, som er støttet af Novo
Nordisk Fonden med 6 mio. kr., ønsker vi – med afsæt i og aftryk tilbage
til matematikfaget – at styrke gymnasieelevers kompetencer inden for
kunstig intelligens og de muligheder, som teknologien rummer. Torben
Tvedebrink, Mikkel Meyer Andersen og Lisbeth Fajstrup fra Institut for
Matematiske Fag, Aalborg Universitet, skal i projektet samarbejde med
de fem aalborgensiske stx-gymnasier (Hasseris, Katedralskolen,
Aalborghus, City og Nørresundby) om at udvikle et undervisningsforløb
som kombinerer AI og matematik, således at eleverne både får indsigt i
mulighederne med AI og styrker deres matematiske kompetencer.

Eleverne får mulighed for at se, hvor centrale matematiske begreber og
værktøjer er i udviklingen af avancerede AI-metoder og -algoritmer.
Projektet kommer til at styrke forståelsen af matematiske
funktioner og matematisk modellering.
Viden om hvorfor matematiske modeller er
nødvendige for at opnå indsigt i de komplekse, stigende datamængder,
styrkes sammen med evnen til at kunne navigere i strømmen af nyheder
baseret på sådanne modeller anvendt på data.

I “AI – Aalborg Intelligence” vil vi udvikle undervisningsressourcer i
form af noter, videoer og online interaktive apps sådan at
gymnasieeleverne selv kan lege og eksperimentere med AI-metoder. Ved
at “sætte vinduer i de sorte bokse” vil vi i de udviklede apps
tydeliggøre hvordan matematikken aktivt bruges i modelleringen af
data. Det vil være med til at gøre den abstrakte matematik mere
konkret og styrke motivationen for at tilegne sig de fornødne
matematiske kundskaber.

Ved afslutningen af det 4 årige projekt vil vi have udviklet et
undervisningsforløb, der kan inddrages i de eksisterende undervisningsplaner,
og som vil kunne udbredes til alle landets gymnasier.

Vi kan slet ikke vente med at komme i gang!

Torben, Mikkel og Lisbeth.

Tidlige computerspil var “flade” – karakterne kunne hoppe over, men ikke “til siden”. Nu er de naturligvis rumlige – på den flade computerskærm. Man kan så gå udenom i stedet for at forsøge at hoppe over. Men man kan stadig være fanget i et låst lokale. Hvis man har en fjerde dimension kan man bruge den til at “gå udenom”. Det er der nogen, der har lavet spil med – her er et forsøg, som muligvis ikke er realiseret:

Matematikere og anvendere af matematik har ikke noget problem med at tale om eksempelvis data i dimensioner højere end 3. For en gymnasieelev kan det lyde meget besynderligt og mange spørger “Er den fjerde dimension så tiden?” Men for daglige brugere af  modeller for fysik, biologi, økonomi og helt generelt højere dimensionalt data, er det slet ikke noget, vi overvejer.

Et punkt (1,-3,7,0,534,14) ligger for os i dimension 6, det 6-dimensionale rum. Der er nemlig 6 koordinater.  Vi kalder dette rum for (udtales “r seks” og ikke “r i sjette”) At vi så ikke lige kan tegne det ind i et koordinatsystem er en anden sag. Man kan sagtens regne med 6 koordinater uden at tegne. I det følgende tænker jeg ind imellem på sådan et punkt som en vektor – fra Origo til (1,-3,7,0,534,14) – og ind imellem som et punkt.

Nedenunder er a = og b=

Addition og multiplikation med en skalar (et tal):

(her er k et reelt tal.)

Afstand, vinkler, indre produkt.

Der er flere afstandsbegreber (metrikker), men den historie får I en anden gang. Her går vi med den Euklidiske version, som er den, de fleste er vant til. Jeg skriver alt i dimension 6, men det er naturligvis samme historie i dimension 238:

Skalarprodukt (indre produkt): – gang koordinater sammen parvis og læg resultaterne sammen.

Længden 

Afstand: Afstand mellem punkter er længden af vektoren, der forbinder dem: 

Vinkler: Vinklen v mellem a og b kan findes udfra

Kugler og kuber.

Cirkler i planen og kugleflader i rummet med centrum C og radius r, er begge karakteriseret ved, at det er du punkter, der har  afstand r til et punktet C. Det kan umiddelbart generaliseres:

Kuglefladen med centrum i C=(c_1,c_2,\ldots,c_6)  og radius r er de punkter, der opfylder Med centrum i Origo og radius 1 får vi

, de punkter i , som har længde 1. Hvorfor og ikke ? Fordi sådan en kugleflade har en dimension mindre – ligesom man kan have planer i . Den historie må også vente… Kuglefladen i er altså og er en cirkel.

Rektangler og kasser kan også fint generaliseres. De punkter, der opfylder er en kasse, et hyperrektangel om man vil.

Der er mere om kugleflader (kugler) i blogindlægget om kuglepakninger

Den “tesseract”, der vises i filmen ovenfor, er en kube i , en hyperkube. Altså punkter , hvor alle koordinater ligger mellem 0 og 1. Ydersiden af sådan en kube er der, hvor mindst en af koordinaterne er enten 0 eller 1. En sædvanlig kube har 6 sideflader:      .

En hyperkube har 8 kuber på sin “overflade”:  ,  . De hænger sammen – ligesom sidefladerne på en sædvanlig kube. Man kan selvfølgelig ikke se det i vores sædvanlige dimension, men man kan lave en film, hvor man ser projektionen af en roterende hyperkube:

En sædvanlig kube, der roterer kan vores hjerne straks lave 3d, selvom den er på en 2d skærm:

Kurver og kontinuitet.

Det går jo fint med at generalisere det, vi kender fra plan og rum. Nu prøver vi med kurver. vi skal jo snyde i et spil og komme ud af et lukket rum ved at bruge en dimension mere.:

En parametriseret kurve i er en funktion ,  , funktionen tager én koordinat ind og giver n koordinater ud. Man kan også sige, at den består af n koordinatfunktioner.

Kontinuitet: Gymnasieintuitionen om “ikke at løfte blyanten” har det svært, når blyanten skal tegne noget i højere dimensioner. I får definitionen at tygge på, men faktisk kan jeg nøjes med sige ,  er kontinuert, hvis alle koordinatfunktionerne er kontinuerte.

Her er definitionen: ,  er kontinuert i $t_0$, hvis der til ethvert findes et , så   garanterer, at

Jeg illustrerer, hvordan man kommer ud af et kugleformet rum – I kan selv oversætte til noget med kasser:

Hvis en 2d-computerspilsfigur er spærret inde i cirklen og kun kan bevæge sig i planen, så kan den ikke komme ud (uden at krydse gennem cirklen): Lad os antage, jeg har bevæget mig ud langs kurven  startende med t=0 sluttende med t=1. Det er en kontinuert kurve (ellers kan alt lade sig gøre i det computerspil 🙂 ).

Så er , fordi jeg begynder indenfor cirklen. Og , fordi jeg ender udenfor. Nu påstår jeg, at der er et tidspunkt , hvor . Hvorfor? Jo, den sammensatte funktion er kontinuert og g(0)<1, g(1)>1. Så siger mellemværdisætningen, at der findes , hvor .

Hvis den 2d-computerspilsfigur får sig en ekstra dimension, så kan den komme ud – den hopper over kanten:

• Lad os starte i (0,0), som nu udvides med en dimension – vi starter i (0,0,0).
• Første del af kurven er r(t)=(0,0,t) for t mellem 0 og 1.
• Næste del er r(t) = (t-1,0,1) for t mellem 1 og 3 – nu er vi kommet til punktet (2,0,1).
• Sidste del er r(t)= (2,0,4-t) for t mellem 3 og 4. Nu er vi i punktet (2,0,0) og vi folder den tredie dimension sammen igen.

Jeg passerer naturligvis igen et sted, hvor |r(t)|=1, men det er i punktet (0.0.1), som jo ikke ligger på cirklen. Jeg hopper over.

Hvis jeg er lukket inde i kan jeg komme ud med samme trick: Jeg starter i (0,0,0). Folder min fjerde dimension ud og er nu i (0,0,0,0). Den kontinuerte kurve ud er

• (0,0,0,t) for t mellem 0 og 1. Så er vi i (0,0,0,1)
• (t-1,0,0,1) for t mellem 1 og 3. Så er vi i (2,0,0,1)
• (2,0,0,4-t) for t mellem 3 og 4. Vi ender i (2,0,0,0) of folder den fjerede dimension ind igen.

Der er naturligvis et tidspunkt, hvor |r(t)|=1, nemlig i punktet (0,0,0,1), men det er ikke på , som er punkter  (x,y,z,0). Jeg er “hoppet over” via den fjerde dimension.

Har man knuder på snørebåndene eller på sit strikkegarn, kan man også have nytte af en fjerde dimension. Der kan alle knuder løses op…

I årets valgkamp ville Ekstrabladet have politikere til at underkaste sig en løgnedetektor. Det ville politikerne ikke – og det er der mange gode grunde til. En af dem er, at løgnedetektorer ikke virker. Det er ellers så smart i de amerikanske film, i talkshows og andre steder, at man kan finde “sandheden” med sådan en test. Men det er der ikke noget belæg for. (Nedenstående er en delvis genudsendelse fra Numb3rs-bloggen, men mon ikke, mange har glemt det indlæg…)

I bogen The Lie behind the Lie detector er en lang udredning om problemerne ved løgnedetektorer. Man kunne ellers forestille sig at man ret let kunne lave kontrollerede forsøg, eller undersøge noget af alt det data, man har fra allerede udførte løgnedetektioner, og det har man  også gjort, men det giver ikke gode resultater. Problemet er bl.a., at de fysiologiske reaktioner, man måler, også kan komme fra andet, end at man lyver. Og det er meget vanskeligt at skille ad. Og så er vi jo et stykke væk fra noget objektivt. Se også The polygraph and lie detection.
Et andet problem er, at forskellige personer fortolker et løgnedetektorudkrift forskelligt – i en Nature artikel fra 1984 tog man 207 udskrifter fra løgnedetektorer i en stribe senere opklarede sager og fik dem analyseret af 14 andre løgnedetektoreksperter. Det gav dom til 43 % af de uskyldige og frikendelse til 36 % af de skyldige…

Det er selvfølgelig værst, at man risikerer at dømme en uskyldig, men i andre lignende situationer kan både falske positive og falske negative være problematisk. Tester man for en sygdom kan det være lige problematisk at sende raske personer igennem en behandling med bivirkninger som at overse nogen, som er syge.

Hvordan ved man, om en test er god?

En test for en sygdom skal jo finde de syge, men helst ikke udpege for mange raske som værende syge. Lad os sige, man har en positiv test, hvis den viser, man er syg.

Der er et antal falsk positive FP (raske, som tester positivt)

Et antal falsk negative FN (syge med en negativ test)

Et antal sandt positive SP( De syge med positiv test)

Og et antal sandt negative SN (raske med negativ test)

Specificitet er , andelen af de raske, som tester negativt, altså sandsynligheden for at testen viser, man er rask, givet man er rask,  P(testrask|rask).
Sensitiviteten er , andelen af syge, der tester positivt P(testsyg|syg).

Vi er mere interesserede i “den anden vej”:

Den positivt prædiktive værdi er , andelen af positivt testede, som rent faktisk er syge, sandsynligheden for at være syg, når testen viser, man er det, P(syg|testsyg).
Eller, man kan se på den negativt prædiktive værdi , andelen af negativt testede, der rent faktisk er raske P(rask|testrask).
De prædiktive værdier afhænger af, hvor stor en andel af de testede, der er syge, prævalensen. Og ikke kun af sensitivitet og specificitet.

Eksempel: En test har sensitivitet 0,86 og specificitet 0,92

På et hospital henvises folk, som mistænkes for at have  sygdommen, til test. På et andet er det en test, der laves på alle. Prævalensen i det første tilfælde er altså højere end i det andet tilfælde.

På Hospital 1 er 37 ud af 49 patienter syge. (Prævalensen er 37/49=0,76)

SP=0,86×37=32,
SN=(49-37)x0,92=11,
FP=12-11=1,
FN=37-32=5.

Specificitet SN/(SN+FP)=11/12=0,92

Sensitivitet SP/(SP+FN)=32/37=0,86

Positiv prædiktiv værdi SP/(SP+FP)=32/33=0,97

Negativ prædiktiv værdi SN/(SN+FN)=11/16=0,69

På Hospital 2 er 37 ud af 157 syge. Prævalens 0,24

SP=32, SN=110, FP=10,  FN=5,

Specificitet SN/(SN+FP)=110/120=0,92

Sensitivitet SP/(SP+FN)=32/37=0,86

Positiv prædiktiv værdi SP/(SP+FP)=32/42=0,76

Negativ prædiktiv værdi SN/(SN+FN)=110/115=0,96

Hvis man tester en stor befolkningsgruppe med få syge, vil den negative prædiktive værdi være stor, i.e., hvis man tester negativt, er man med stor sandsynlighed rask. Men dem, der tester positivt vil i mange tilfælde være raske, i.e., sandsynligheden for at være syg givet testen viser syg, er lille. (Tallene er fra How sensitive is sensitivity, how specific is specificity, Phillips, Scott og Blasczcynski, American Journal of Roentgenology. Prøv selv at regne på, hvod der sker, hvis der er 37 syge ud af 12037. Så bliver positiv prædiktiv værdi 0.03 og negativ prædiktiv værdi 0,99. Der er altså rigtig mange blandt dem, der tester positivt, som alligevel er raske – her 97 ud af 100. Det er det, man skal overveje, når man laver store screeninger for sygdomme. Der er flere raske, som skal undersøges yderligere, måske behandles og i hvert fald bliver unødigt bekymrede.

På Understanding Uncertainty er der en fin animation af andre eksempler.

Løgnedetektorer igen.
Lad os nu antage, at de kan finde løgnere med en vis sandsynlighed (det kan de ikke, men alligevel…). Tester man alle, der ansøger om job i FBI, CIA,… og det gør man…vil dem, der ser ud til at lyve, stadig med ret stor sandsynlighed tale sandt. I.e., mange får et stempel som spion, uden at være det. Dem, der udses som ikke værende spioner, er det med ret stor sandsynlighed ikke, men det er mere fordi, der er rigtig mange, der ikke er spioner, end fordi man er god til at finde spioner. Der vil jo stadig være en enkelt spion der slipper ind nu og da.

Vi kan være glade for, at vi ikke bruger metoden til noget seriøst i Danmark og håbe på, det forbliver noget, der hører til pjattede TV-programmer. Så fans af Doctor Phil eller  andre populære brugere af løgnedetektorer bør tage det med et gran salt. Udover det helt oplagte, at sårbare mennesker ikke bør være underholdning. Men det er ikke matematik – bare almindelig ordentlighed.

Tirsdag blev årets Abelprisvinder annonceret i en live streamet begivenhed i Oslo.

Karen K.Uhlenbeck får prisen for sit nybrudsarbejde (de skriver “nybrottsarbeid” på norsk) indenfor geometriske differentialligninger, gaugeteori og integrable systemer. Og for den fundamentale indflydelse, hendes arbejde har haft i analyse, geometri og matematisk fysik.

Her fortæller Karen Uhlenbeck om Emmy Noethers arbejde. (Foto Andrea Kane, IAS,Princeton) Noether var  i 1928 en af hovedforedragsholderne ved den internationale kongress for matematiker, ICM. Den næste kvinde i rækken af hovedforedragsholdere ved ICM var Karen Uhlenbeck i 1990.

Karen Keskulla Uhlenbeck (f. 1944) har, ligesom de andre Abelprismodtagere, haft en lang karriere i matematik og der er mange fine interviews og portrætter af hende på nettet. På Celebratio.org er hun  portrætteret i et fint interview af Allyn Jackson. Der er i øvrigt andre fine matematikerportrætter.

Jeg kender Uhlenbecks matematik fra da jeg i mit speciale beskæftigede mig med Gaugeteori. Uhlenbecks “bubbling” var helt centralt i det, der dengang var det hotte emne, 4-dimensionale mangfoldigheder og nye ideer, som forbandt forskellige områder af matematik og Gaugeteori fra fysik. Jeg vil (og kan) ikke forklare Uhlenbecks arbejde i detaljer, men nybrud, som Abelpriskommiteen kalder det, er en god overskrift.

Minimalflader, variationsregning og bobler/instantoner.

Minima og maksima for funktioner kendes fra gymnasierne. Man skal differentiere funktionen og finde nulpunkter.

Variationsregning er et skridt videre: Det, der skal minimeres er et funktional, som er en funktion, hvis input er andre funktioner. Det klassiske eksempel er det brachistochrone problem: Lav den hurtigste kuglebane mellem to punkter. Kuglen lægges i det øverste punkt og er kun påvirket af tyngdekraften, mens den ruller til det andet punkt. Man ville måske gætte på en linje – det er sådan en pæn kurve – men den blå kurve nedenfor giver svaret.

Man skal altså se på alle de kurver, der findes fra A til B – kurverne er de variable, funktionen er den samlede tid.

Mere generelt ser man på den samlede energi. Der er her vide rammer for, hvad energifunktionalet kan være. Man kan faktisk også her differentiere og finde nulpunkter for den afledede, men det kræver mere maskineri. Og man får bragt partielle afledede ind i billedet.

Uhlenbecks PhD-afhandling, “The calculus of variations and global analysis”, 1968, er i dette område.

Mens det brachistochrone problem drejer  sig om alle kurver mellem to punkter, kan man i stedet se på flader (2-dimensionale objekter) mellem givne randkurver (tænk på sæbehinder)

OBS: Det er ikke det, der er Uhlenbecks “bubbling”.

Man leder her efter fladen med mindst areal. Trækker man ringene langt fra hinanden, får man to sæbehinder – en i hver ring.

I det mere generelle problem, som Uhlenbeck og Jonathan Sacks løste, har man flader i mere komplicerede rum end vores sædvanlige Euklidiske. En flade er da en funktion fra kuglefladen til dette mere komplicerede rum. De konstruerer en følge af sådanne afbildninger, som allesammen er “pæne” og kommer tættere og tættere på en ny flade – en grænse for følgen. Matematikstuderende har set den slags grænsefunktioner i indledende analyse.

Grænsefladen er en funktion, som er pæn, bortset fra i et endeligt antal punkter, singulariteter. Tæt på singulariteterne har man “bubbling”. Arealet af grænsefladen er mindre end forventet – det er ikke grænsen for arealerne af følgen. Noget af arealet er boblet af – som et stykke tyggegummi.

Metoden og ideerne har haft enorm indflydelse – grænser, der kan kontrolleres, bortset fra i endelig mange punkter, er ikke så ringe endda. Og bubbling giver en forståelse af singulariteterne.

Gauge Teori

(udtales som en engelsk port, “gage”) drejer sig i fysik om de fænomener, som ikke ændrer sig, selvom man skifter “koordinatsystem” – laver en gaugetransformation. Fysikerne Yang og Mills fik i 1999 Nobelprisen for det, de i 1954 havde foreslået som en model for den svage vekselvirkning og som udvidede de hidtil brugte “koordinatskift” (til ikke-abelske grupper for de indviede).

Det, der skal være uafhængigt af valg af koordinatsystem er nogle partielle differentialligninger.

Invarians under koordinatskift – et simplere eksempel:

“Vindretningen er NNØ (Nord Nord Øst), hvor jeg står” giver kun mening, hvis jeg har et koordinatsystem med retningerne. Men vinden har den retning, den har.

Står man på Nordpolen, given NNØ ikke mening – der skal bruges flere koordinatsystemer for at beskrive retninger på Jorden, og tilhørende “oversættelser” fra et koordinatsystem til et andet.

Tilbage til Gaugeteori. Den kombination af partielle differentialligninger (Yang Millsligningerne)  og geometri (kugleflader, mere komplicerede flader og lignende højeredimensionale objekter – mangfoldigheder) kræver nye metoder og mod til at gøre noget i det ene matematiske område, som man aldrig har prøvet før. Uhlenbeck gav matematisk fast grund under fødderne i studiet af Yang Mills ligningerne. Bl.a. er bubbling fundamentalt. Uhlenbeck forklarer selv i interviewet med Allyn Jackson, at bubbling fungerer, når man har et problem, der er invariant under skalering – noget, hun allerede havde klarlagt i sin phd-afhandling.

Som den skarpsindige læser vil se, er Uhlenbecks arbejde ikke let at forklare. Hun har arbejdet mellem matematiske områder og kastet sig ud på det dybe vand imellem områderne.

Karen Uhlenbeck i Berkeley i 1969.

En anden side af Karen Uhlenbeck er hendes arbejde for at give matematikken videre. Hun startede, sammen med Dan Freed i 1996 Park City Mathematics Institute, PCMI, hvor bl.a. gymnasielærere og matematikere mødes. Det er flere parallelle sommerskoler og har haft stor betydning for mange, som er mødtes der. Der er en forskningsdel for phd-studerende og der er fokus på at give minoriteter i faget mulighed for at få fodfæste.

Karen Uhlenbeck har haft enorm indflydelse i både matematik som fag og blandt matematikere, og potentielle matematikere, hvor hun siger, hun håber, hun kan være rollemodel for de skæve eksistenser. Hun er rollemodel for mange, hun er en matematisk superstjerne og nu får hun Abelprisen. Det er jeg meget begejstret for.

Læs mere i Quanta Magazine  og på Abelprisens sider. Der er mange andre, men dem finder I nok, når I Googler.

Jeg er lidt sent ude, men det bliver jo jul alligevel.

Der kommer ikke julekalender her på bloggen. Men der er heldigvis andre, der tror, de kan holde dampen oppe og poste 24 indlæg med matematik. Så her skyder vi genvej og henviser til andre.

Først på tysk Mathe im Advent
Man skal vistnok tilmelde sig.
The Aperiodical har selvfølgelig en julekalender. Der er mange fine matematikhistorier og opgaver. Og naturligvis Møbiusbånd.

Matthew Scroggs, endnu en matematikformidler i Storbritannien, har opgaver og hovedbrud.

Plus Magazine har en. Med Podcasts.

Transum, som jeg ikke kendte i forvejen har også en – med opgaver.

Og så noget matlabkode forklædt som juletræ:

Koden finder I her.

I kan vælge forskellige parametre. Hvor mange kugler skal der på? Hvor skinnende skal kuglerne være… Uhyre nyttigt 🙂

En artikel i Nature Communications om et “nyt matematisk objekt” har givet genlyd. Scutoiden hedder den lille ny. Den kan ses på figur d, hvor to scutoider passer sammen (den grønne og den gule)

Illustration fra Nature Communications.

Scutoider er (op)fundet af en gruppe forskere – biologer, dataloger, matematikere, som ville forstå, hvordan visse typer væv, epithelvæv, er opbygget. Den slags væv er lagdelt – eller pakket mellem nogle lag. Ifølge artiklen i Nature, er der epithel-celler, som forbinder celler i to (flade) lag. Det har man bl.a. set i bananfluer – drosophila.

Billede fra Wikipedia – cell junctions.

Hvis lagene ikke krummer, er der allerede en fin model, hvor de to lag forbindes med prismer og keglestubbe (a og b på første figur – frustrum er keglestub).

Men hvad nu, hvis lagene krummer? Som eksempelvis når væv er afgrænset omkring en blodåre, tarmene eller noget i den retning?

I hvert afgrænsende lag danner cellegrænserne Voronoiceller:

 De røde prikker er centre. Et punkt i en “celle” ligger tættere på det røde punkt i cellen end på noget andet rødt punkt.

Sådan er det altid – uanset, om lagene krummer eller ej. Nu skal to sådanne lag forbindes. I modellen skal der laves en forbindelse fra hver Voronoicelle i det ene lag til hver Voronoicelle i det andet, som man ser i a) og b) i første figur. Når lagene er plane, har man hidtil kunnet gøre det med keglestubbe og prismer – fordi man i det tilfælde har lige mange kanter langs matchende Voronoiceller i de to lag.

Forestiller vi os nu, at de to lag er cylindriske med forskellig radius som i c) og desuden for at gøre det simplere, at cellekernerne ligger “samme sted” bortset fra radiuskoordinaten – mere præcist: Punkter i rummet kan beskrives med en radius, vinkel og en højde. Figuren nedenfor viser radius, vinkel og højde . Cellekernerne på de to forskellige cylindere har altså samme , men forskellig

Hvad sker der så med Voronoicellerne? Bliver de ikke bare “ganget ud” med radius? Nej! For afstande mellem punkter på cylinderne bliver ikke bare ganget:

Afstande på en cylinder kan findes ved at “rulle cylinderen ud” til et rektangel og måle i planen.

Er cylinderen h høj og har radius r, er rektanglet h på den ene led og på den anden. Med samme højde og radius R er det h på den ene led og på den anden. Og så ændrer Voronoicellerne sig kvalitativt. På billederne nedenfor, som Jakob Gulddahl Rasmussen har lavet til mig, er 6-kanten omkring det midterste punkt blevet til en 4-kant, når der strækkes på den ene led. Linjestykkerne er midtnormaler mellem par af punkter (på linjestykket er der lige langt til to af “cellekernerne”) og de slutter, når de møder andre midtnormaler. I kan lege med, hvordan det ændrer sig, når man strækker på den ene led, eller  når man flytter  i en af de mange apps, der findes. Her er en på University of Michigan. – Se mere på Numb3rsbloggen

Og så kommer problemet: Man skal indsætte en forbindelse mellem celler med forskelligt antal kanter. Det kan ikke være en keglestub eller et prisme, for de har samme antal kanter i øverste og nederste flade. Det er her Scutoiden skal bruges. I figuren øverst ser man scutoider mellem femkanter og sekskanter. Den ene kant i scutoiden deler sig et stykke nede i to kanter. (Hvis man flytter delepunktet helt ned (eller op), får man et prisme, men det er ikke sådan, vævet opfører sig.)

Scutoidens sider er ikke plane – de krummer. Men det har vist sig, at det er sådan, det ser ud, når man kigger nærmere på en bananflue, eller hvad man nu har.

Scutoider bruges nu til at lave modeller for epithelvæv. Man gætter på, at de kan bruges til at lave kunstigt væv.

Man kan købe 3d-printede scutoider, der er artikler om scutoider her, der og allevegne. Jo, den lille ny er berømt.

Selvfølge har den uforlignelige Matt Parker lavet en video om scutoider. Med piberensere… Og interview med matematikeren bag.

Om det er ny matematik, kan man bestemt godt diskutere. Men det er ny indsigt og giver nye anvendelsesmuligheder i et samarbejde mellem mange fagområder. Det er da helt fremragende!

Det er sommer og der er stilhed på bloggen. Mens I venter er her et tilbud:

På The Aperiodical har de The Big Internet Math-Off – inspireret af VM i fodbold, I presume. Det er knock out fra begyndelsen af. To matematikformidlere fortæller om deres yndlingsmatematik og der kan så stemmes. Her er et forslag: Jeg lover, at vi vil fortælle mere her på bloggen om mindst et af emnerne. (Eller måske bare give en dansk version – det er svært at konkurrere med Matt Parker og co.)

Her er de hidtidige indlæg:

James Tanton mod Nira Chamberlain.

Tanton: Om at skære en kage op og samle den igen og få kage tilovers – og lave uendelig meget kage.

Chamberlain: Om Formel 1 og hvordan Reynoldsligningen sikrer, hjulene ikke falder af.

Samuel Hansen mod Paul Taylor

Hansen: Hvorfor dine venner har flere venner, end du har (Link til Soundcloud) og hvordan det kan bruges til at stoppe epidemier.

Taylor: Hvordan kan man være helt sikker på, Pythagoras’ sætning holder (se linket ovenfor – det er ikke en video.)

Peter Rowlett mod Alison Kiddle

Rowlett: Parabolske kurver – herunder at tegne dem med rette linjer. Og tikz-kode, så du kan gøre det i LaTeX. Også en lille video

Kiddle: Hagas sætning – matematisk origami, om at folde et kvadrat og få delt siderne  i diverse brøkdele Se også Plus Magazine

Edmund Harriss mod Colin Wright

Harriss: Penrose fliselægning. Det har vi haft på bloggen før, men ikke med så fine fliser skåret i træ 🙂

Wright: Tag et spil kort og lav 13 bunker (med 4 i hver). Hvis der er alle kort es, 2,3,…, konge, (ikke nødvendigvis i rækkefølge)  er du færdig. Ellers: Kan du omorganisere hver bunke, så du ender med at have es,to,…, konge øverst? Svaret er, ifølge Wright, altid ja.

Tiago Hirth mod Evelyn Lamb

Hirth: Et rebtrick med Borromeanske ringe

https://youtu.be/RRZqX2hOQvk

Lamb: Wallis’ si og sammenhængen med . (I familie med Sierpinskis tæppe, Mengers svamp,…)  Hun har mere om det på sin blog Det er et af en længere række af yndlingsobjekter (favourite spaces – svært at oversætte)

Matt Parker mod Matthew Scroggs 

Parker: Machine Learning med perler i æsker. En “maskine” lærer at spille kryds og bolle.

Scroggs: Om at spille Asteroids i en kortprojektion (han kalder det Mathsteroids). Blogmosteren her synes, det er supercool, men kortprojektioner er altså virkelig god matematik.

Her er spillet i Mercatorprojekttionen

Der er andre, som er mere udfordrende: Billedet her viser rette linjer i den projektion, der bruges i FNs logo.

FNs logo

James Propp mod Zoe Griffiths

Propp: Om knuder og rebtrick.

Griffiths: Sandsynlihedsteori og placering af passagerer i et fly

Jo Morgan mod Tony Mann

Morgan: Hexaflexagons. Med link til Vi Harts videoer om netop det. De har danske undertekster!

Mann: Om tilfældige tal og at score 100% til enhver eksamen (Njah, mon dog)

Vælg to hele tal p og q, som er parvis primiske (det eneste tal, der går op i både p og q er tallet 1). Tegn cirklen i planen med radius og centrum i . Bed nu en anden om at gøre det samme – med nyt valg af p og q. De to cirkler vil tangere x-aksen og enten tangere hinanden eller ikke have noget til fælles. Bliv ved og der opstår et fint mønster af cirkler. De kaldes Ford-cirkler, fordi de blev beskrevet i en artikel i American Mathematical Monthly i 1938 af Lester R. Ford Sr.

Notation: Fordcirklen svarende til p,q kaldes C(p,q).

Her på figuren er valgt , så og dermed er x-koordinaten for centrum mellem 0 og 1. Tallet i cirklen er x-koordinaten for centrum (forkortet, så det svarer til p/q). Farven indikerer nævneren p.

Her er nogle konstateringer:

• Ethvert rationalt tal a/b på x-aksen bliver rørt af en Fordcirkel: Forkort a/b og lav så Fordcirklen.
• Radius og dermed højde af C(p,q) afhænger kun af q.

To Fordcirkler skærer ikke hinanden:

To Fordcirkler C(p,q) og C(r,s) vil enten tangere (kysse kaldte jeg det i indlægget om kuglepakninger) eller slet ikke røre hinanden:

De har centrum i hhv.  og  så afstand mellem centrene opfylder

Summen af de to radier er

Nu sammenligner vi d og s ved at udregne . Hvis de to cirkler skærer hinanden er  . Tangerer de, er .

====

Forskellige Fordcirkler skærer ikke:

Hvis de to cirkler skærer, er
og altså 

Men  ps – rq  er et helt tal, så det vil kræve
ps – rq = 0 og altså  ps = rq ,
så
og altså er det samme cirkel.

Fareyfølger.

Hvis C(p,q) og C(r,s) tangerer, er |ps-rq|=1. Det leder til en anden pudsig observation. men først skal vi have indført brøkregning a la Farey:

Dette er de første Fareyfølger

Fareyfølgen er uforkortelige brøker mellem 0 og 1 med nævner højst n. Rækkefølgen er efter størrelse. De elementer, der tilføjes til for at få er medianten af naboerne:

I tilføjes . Naboerne er . Medianten er dårlig brøkregning, Fareyplus:

Her er det tilsvarende for Fordcirklerne

Hvorfor gælder det? Her er først nogle konstateringer:

1. Hvis ligger medianten imellem dem . Man viser det første ulighedstegn som følger:  og det følger af .
2. Medianten mellem to naboer i tilføjes i skridtet fra til , når nævneren den forkortede brøk svarende til er højst n+1.
3. Medianten af to naboer i en Fareyfølge er uforkortelig: Medianten er ikke i , da er naboer. Antag  og $\frac{q}{p}$ er uforkortelig. Så er p>k, da medianten ikke er i . rp=b+d og . Altså er r=1.

Medianten tilføjes altså i skridtet fra til .

Nu mangler vi blot at se, at alle uforkortelige brøker kommer med i en proces, hvor vi begynder med og tilføjer medianter.

Stern Brocot-træet.

Lad os undlade at holde styr på, hvor store nævnerne er. Så bygger vi Stern-Brocot-træet (opkadt efter Moritz Stern, matematiker, og Achille Brocot, urmager (!) ):

Vi bruger kun den venstre side. De stiplede linjer hjælper til at se, hvad der tages medianter af, men et lag eller “niveau” er kun de sidst tilkomne.

Påstand: Alle uforkortelige brøker kommer med i et lag i træet. (Og det er derfor ok at konstruere Fareyfølger via medianter.)

Først er hjælperesultat: Hvis er barn og forælder eller forælder og barn i træet (forbundet med en kant opad eller nedad fra  til $latex  \frac{c}{d}$, så er . Bevis: Induktion. Det er ok for 0/1 og 1/1. Hvis ok for , så er det ok for kanter til og fra medianten: Der er enten en  kant nedad mellem  eller opad .
pr antagelse. Og tilsvarende for den anden side. (Lav selv et særargument for medianterne med hhv. 0/1 og 1/1.) En konsekvens er, at afstanden er  .

Argument for, at alle uforkortelige brøker er med i Stern-Brocot-træet: : På det k’te niveau i træet er summen af nævner og tæller i brøkerne mindst k+2, da Niveau k fremkommer som medianter fra niveau k-1 og højere niveauer. (Der laves hele tiden medianter med 0/1 og 1/1).

Antag nu, at p/q ikke er med i træet. Specielt er den ikke med på niveau p+q-1. Men den ligger mellem to naboer (forbundet med en kant), hvor den ene er på niveau p+q-1: . Omskriv de to uligheder til

og . Det er hele tal, så vi kan skrive begge steder.

Heraf: (Det sidste følger af, at den ene brøk er fra niveau p+q)

Udregn venstresiden og brug bc-ad=1, da disse er forælder og barn i træet. Venstresiden giver da p+q. Og vi har en modstrid.

Tilbage til Fordcirklerne:

To Fordcirkler C(p,q) og C(r,s) tangerer hvis og kun hvis |ps-rq|=1. Altså svarer brøker, som er naboer i en Fareyfølge til tangerende Fordcirkler. Og det gælder også omvendt, men det har vi ikke vist her.

Endnu et pænt billede. His Fordcirklerne skærer, så vil halvcirklen fra (p/q,0) til (r/s,0) passere skæringspunktet.  Farven på halvcirklerne svarer til den Fareyfølge, hvori brøkerne er naboer.

I 1967 skrev den dengang 31-årige Robert P.Langlands et 17 sider langt brev til André Weil. Weil var 30 år ældre og en af den tids store og indflydelsesrige matematikere. De to mødte hinanden, da de ventede på at komme ind til et foredrag, Langlands gav sig til at fortælle om nogle ideer og Weil foreslog ham at skrive dem ned. Måske for at slippe væk… Weil inviterede desuden Langlands til at besøge ham på Institute of Advanced Studies, Princeton og det lange brev skrev han inden besøget. Billedet her viser, hvad Langlands skrev på forsiden:  ”In response to your invitation to come and talk I
wrote the enclosed letter. After I wrote it I realized
there was hardly a statement in it of which I was certain.
If you are willing to read it as pure speculation
I would appreciate that; if not – I am sure you have
a waste basket handy.”

Weil fik renskrevet de 17 sider – på skrivemaskine – og det er det, derblandt matematikere kaldes Langlandsprogrammet.

Nu får Langlands  Abelprisen for sine “spekulationer”! Han har naturligvis selv bevist matematiske resultater, men priskomitéen skriver, han får prisen for “sit visionære program, der forbinder repræsentationsteori og talteori.”

Langlands på en konference i 2016. (Dan Komoda/Institute for Advanced Study)

Langlandsprogrammet indeholder nogle formodninger (conjectures) og et program for, hvordan man bør kunne bevise, at disse er korrekte. Det drejer sig om nogle forbindelser mellem områder af matematik, som ellers er ret forskellige i både emneområde og metoder. Den slags forbindelser giver sædvanligvis anledning til rigtig mange nye indsigter i begge områder. Lad mig forsøge at kaste lys på et lille hjørne af, hvad det går ud på:

Nogle primtal kan skrives som en sum af to kvadrattal:

Hvis man ser bort fra 2 (vi skriver “for et ulige primtal”, men der betyder jo bare, at 2 ikke er med) har alle disse primtal en fælles egenskab: Et primtal p, som ikke er 2, kan skrives som en sum af to kvadrattal hvis og kun hvis , hvor k er et naturligt tal. Det beviste Euler. Det er et eksempel på en reciprocitetslov – en egenskab ved primtallene udtrykkes ved division med rest . Her er det division med 4, som skal give rest 1. Vi skriver

Et komplekst tal kaldes et Gaussisk heltal, hvis er hele tal. Hvis , så er ( husk, og så er resten givet ved at gange ind i paranteser) og omvendt. Et primtal p er et produkt af to Gausisske heltal hvis og kun hvis det er en sum af to kvadrattal. 

De Gaussiske rationale tal er tal , hvor a og b er rationale tal (kan skrives som en brøk , hvor c og d er hele tal. Ganger, dividerer, adderer eller subtraherer man to Gaussiske rationale tal med hinanden, er resultatet rationalt. De Gaussiske rationale tal udgør derfor ikke bare en delmængde af de komplekse tal, men et legeme. Man kan se det som en udvidelse af de rationale tal – man tilføjer og reglen og “beholder” regnereglerne. Det kaldes en legemsudvidelse. 

Nu ser vi på symmetrier.
Hvilke afbildninger har vi , som er lineære: f((a+bi)+(c+di))=f(a+bi)+f(c+di) og bevarer produktstrukturen f((a+bi)(c+di))=f(a+bi)f(c+di) og desuden opfylder f(a+0i) = a+0i. Der er kun to afbildninger: Identitetsafbildningen f(a+bi)=a+bi og g(a+bi)=a-bi.

Da g(g(a+ib))=a+ib (man får skiftet fortegnet to gange), udgør funktionerne f og g en gruppe og g har orden 2 – sammensæt den med sig selv to gange, så får man identiteten.Det er Galoisgruppen for legemsudvidelsen  over .

Tilsvarende kan man se på Galoisgruppen for andre udvidelser af de rationale tal. Tænk på  som en udvidelse af med rødder i og dermed kvadratrødder af alle negative rationale kvadrattal. Vi ved, at alle andengradspolynomier med rationale a,b,c, har to rødder (mere præcist, kan skrives med  og en formel for disse rødder kan skrives blot med brug af kvadratrodssymbolet.

Alle tredjegradspolynomier med rationale koefficienter har rødder, som kan opskrives ved brug af kvadratrødder og kubikrødder. Tilsvarende for 4.gradspolynomier, når man tilføjer fjerde rødder. Men for femtegradspolynomier går det galt. Det viste Abel og Galois. Det er altså ikke nok at kunne løse ligninger for at kunne løse alle femtegradspolynomieligninger. Det mere generelle spørgsmål er, om der er en sammenhæng mellem løsninger til et polynomium og et andet .

Man kan formulere resultatet om primtal som sum af kvadrattal via Galoisgrupper. For et (ulige) primtal p er , hvis og , hvis . Funktionen kaldes en Frobeniusafbildning og er et element af  Galoisgruppen. Frobeniusafbildningen er forbindelsen mellem “kan man skrive p som en sum af to kvadrattal” og  “hvad er “.

Tilsvarende spørgsmål. Polynomiet har rod 1, når man regner modulo 3, da  . Men 1 er ikke en rod modulo 5. Hvor meget information er der i, at kende antallet af rødder modulo  primtal? Og hvad har det med Galoisgrupper at gøre?

Langlandsprogrammet foreslår en vidtrækkende generalisering af dette.

Det giver en forbindelse mellem harmonisk analyse – automorfe former, som er funktioner fra de komplekse tal til de komplekse tal med visse periodicitets egenskaber  –  og rødder i polynomier undersøgt via regning med rest som ovenfor. Andrew Wiles brugte en forbindelse af den type, da han løste Fermats problem.

Jeg har støttet mig til dels informationen på Abelprissiderne nogle noter fra et foredrag at Laurent Lafforgue, som fik Fieldsmedaljen for sit arbejde med Langlandsprogrammet og diverse populariseringer.