Ford-cirkler – og addition af brøker som vor mor IKKE gør det.

Vælg to hele tal p og q, som er parvis primiske (det eneste tal, der går op i både p og q er tallet 1). Tegn cirklen i planen med radius $\frac{1}{2q^2}$ og centrum i $(\frac{p}{q},\frac{1}{2q^2})$ . Bed nu en anden om at gøre det samme – med nyt valg af p og q. De to cirkler vil tangere x-aksen og enten tangere hinanden eller ikke have noget til fælles. Bliv ved og der opstår et fint mønster af cirkler. De kaldes Ford-cirkler, fordi de blev beskrevet i en artikel i American Mathematical Monthly i 1938 af Lester R. Ford Sr.

Notation: Fordcirklen svarende til p,q kaldes C(p,q).

Her på figuren er valgt $p\leq q$ , så $0\leq \frac{p}{q}\leq 1$ og dermed er x-koordinaten for centrum mellem 0 og 1. Tallet i cirklen er x-koordinaten for centrum (forkortet, så det svarer til p/q). Farven indikerer nævneren p.

Her er nogle konstateringer:

Ethvert rationalt tal a/b på x-aksen bliver rørt af en Fordcirkel: Forkort a/b og lav så Fordcirklen.
Radius og dermed højde af C(p,q) afhænger kun af q.

To Fordcirkler skærer ikke hinanden:

To Fordcirkler C(p,q) og C(r,s) vil enten tangere (kysse kaldte jeg det i indlægget om kuglepakninger) eller slet ikke røre hinanden:

De har centrum i hhv. $(\frac{p}{q},\frac{1}{2q^2})$ og $(\frac{r}{s},\frac{1}{2s^2})$ så afstand mellem centrene opfylder

$d^2=(\frac{p}{q}-\frac{r}{s})^2+(\frac{1}{2q^2}-\frac{1}{2s^2})^2$

Summen af de to radier er $s=\frac{1}{2q^2}+\frac{1}{2s^2}$

Nu sammenligner vi d og s ved at udregne $d^2-s^2$ . Hvis de to cirkler skærer hinanden er $d^2-s^2<0$ . Tangerer de, er $d^2-s^2=0$ .

$d^2-s^2$ = $(\frac{p}{q}-\frac{r}{s})^2+(\frac{1}{2q^2}-\frac{1}{2s^2})^2-(\frac{1}{2q^2}+\frac{1}{2s^2})^2$ = $(\frac{p}{q}-\frac{r}{s})^2- 4(\frac{1}{2q^22s^2})$ = $(\frac{ps-rq}{qs})^2- (\frac{1}{q^2s^2})$ = $\frac{(ps-rq)^2-1}{(qs)^2}$

Forskellige Fordcirkler skærer ikke:

Hvis de to cirkler skærer, er
$( ps - rq )^2 - 1<0$ og altså $( ps - rq )^2 <1$

Men ps – rq er et helt tal, så det vil kræve
ps – rq = 0 og altså ps = rq ,
så $\frac{p}{q}=\frac{r}{s}$
og altså er det samme cirkel.

Fareyfølger.

Hvis C(p,q) og C(r,s) tangerer, er |ps-rq|=1. Det leder til en anden pudsig observation. men først skal vi have indført brøkregning a la Farey:

Dette er de første Fareyfølger

$F_1=\frac{0}{1},\frac{1}{1}$
$F_2=\frac{0}{1},\frac{1}{2}, \frac{1}{1}$
$F_3=\frac{0}{1},\frac{1}{3},\frac{1}{2},\frac{2}{3}\frac{1}{1}$
$F_4=\frac{0}{1},\frac{1}{4},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{1}{1}$
$F_5=\frac{0}{1},\frac{1}{5},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{1}{1}$

Fareyfølgen $F_n$ er uforkortelige brøker mellem 0 og 1 med nævner højst n. Rækkefølgen er efter størrelse. De elementer, der tilføjes til $F_n$ for at få $F_{n+1}$ er medianten af naboerne:

I $F_5$ tilføjes $\frac{2}{5}$ . Naboerne er $\frac{1}{3},\frac{1}{2}$ . Medianten er dårlig brøkregning, Fareyplus:

$\frac{1}{3}\oplus\frac{1}{2}=\frac{1+1}{3+2}=\frac{2}{5}$

Her er det tilsvarende for Fordcirklerne

Hvorfor gælder det? Her er først nogle konstateringer:

Hvis $0<\frac{a}{b}<\frac{c}{d}<1$ ligger medianten imellem dem $\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}$ . Man viser det første ulighedstegn som følger: $\frac{a}{b}<\frac{a+c}{b+d}$ $\Leftrightarrow$ $(b+d)a<(a+c)b \Leftrightarrow da<cb$ og det følger af $\frac{a}{b}<\frac{c}{d}$ .
Medianten mellem to naboer i $F_k$ tilføjes i skridtet fra $F_n$ til $F_{n+1}$ , når nævneren den forkortede brøk svarende til $\frac{a+c}{b+d}$ er højst n+1.
Medianten af to naboer i en Fareyfølge $F_k$ er uforkortelig: Medianten er ikke i $F_k$ , da $\frac{a}{b}, \frac{c}{d}$ er naboer. Antag $\frac{a+c}{b+d}=\frac{rq}{rp}$ og $\frac{q}{p}$ er uforkortelig. Så er p>k, da medianten ikke er i $F_k$ . rp=b+d og $b+d\leq 2k$ . Altså er r=1.

Medianten tilføjes altså i skridtet fra $F_{b+d-1}$ til $F_{b+d}$ .

Nu mangler vi blot at se, at alle uforkortelige brøker kommer med i en proces, hvor vi begynder med $\frac{0}{1},\frac{1}{1}$ og tilføjer medianter.

Stern Brocot-træet.

Lad os undlade at holde styr på, hvor store nævnerne er. Så bygger vi Stern-Brocot-træet (opkadt efter Moritz Stern, matematiker, og Achille Brocot, urmager (!) ):

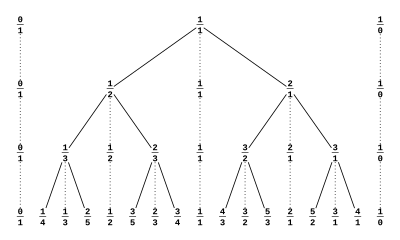
Vi bruger kun den venstre side. De stiplede linjer hjælper til at se, hvad der tages medianter af, men et lag eller “niveau” er kun de sidst tilkomne.

Påstand: Alle uforkortelige brøker kommer med i et lag i træet. (Og det er derfor ok at konstruere Fareyfølger via medianter.)

Først er hjælperesultat: Hvis $\frac{a}{b} < \frac{c}{d}$ er barn og forælder eller forælder og barn i træet (forbundet med en kant opad eller nedad fra $\frac{a}{b}$ til $latex \frac{c}{d}$, så er $bc-ad=1$ . Bevis: Induktion. Det er ok for 0/1 og 1/1. Hvis ok for $\frac{a}{b} < \frac{c}{d}$ , så er det ok for kanter til og fra medianten: Der er enten en kant nedad mellem $\frac{a}{b} < \frac{a+c}{b+d}$ eller opad $\frac{a+c}{b+d}<\frac{c}{d}$ .
$b(a+c)-a(b+d)=bc-ad=1$ pr antagelse. Og tilsvarende for den anden side. (Lav selv et særargument for medianterne med hhv. 0/1 og 1/1.) En konsekvens er, at afstanden er $|\frac{a}{b} - \frac{c}{d}|=\frac{1}{bd}$ .

Argument for, at alle uforkortelige brøker er med i Stern-Brocot-træet: : På det k’te niveau i træet er summen af nævner og tæller i brøkerne mindst k+2, da Niveau k fremkommer som medianter fra niveau k-1 og højere niveauer. (Der laves hele tiden medianter med 0/1 og 1/1).

Antag nu, at p/q ikke er med i træet. Specielt er den ikke med på niveau p+q-1. Men den ligger mellem to naboer (forbundet med en kant), hvor den ene er på niveau p+q-1: $\frac{a}{b} <\frac{p}{q}< \frac{c}{d}$ . Omskriv de to uligheder til

$bp-aq>0$ og $cq-dp>0$ . Det er hele tal, så vi kan skrive $\geq 1$ begge steder.

Heraf: $(bp-aq)(c+d)+(cq-dp)\geq c+d+a+b\geq p+q+1$ (Det sidste følger af, at den ene brøk er fra niveau p+q)

Udregn venstresiden og brug bc-ad=1, da disse er forælder og barn i træet. Venstresiden giver da p+q. Og vi har en modstrid.

Tilbage til Fordcirklerne:

To Fordcirkler C(p,q) og C(r,s) tangerer hvis og kun hvis |ps-rq|=1. Altså svarer brøker, som er naboer i en Fareyfølge til tangerende Fordcirkler. Og det gælder også omvendt, men det har vi ikke vist her.

Endnu et pænt billede. His Fordcirklerne skærer, så vil halvcirklen fra (p/q,0) til (r/s,0) passere skæringspunktet. Farven på halvcirklerne svarer til den Fareyfølge, hvori brøkerne er naboer.