I mandags, 20/3 2023, udkom et preprint “An aperiodic monotile“. Det gav anledning til megen aktivitet på diverse SoMe (i matematikerhjørnerne af SoMe inklusive vores egen FB-side) og i eksempelvis New Scientist. Det er et preprint – det betyder, at det ikke er udkommet i et tidsskrift endnu og at det ikke er igennem peer review, hvor andre eksperter læser det igennem og godkender, at det ser korrekt ud. Så der kan være fejl i, men nu får det alligevel et blogindlæg; forfatterne er i velanskrevne i området, så det er sikkert korrekt. Og der er fire forfattere; de kan nok korrigere hinanden. Nå, nok med forbeholdene. Hvad skal Einstein med en ny hat? Og hvorfor er det interessant.

Hver flise i mønsteret ligner en hat. Det er en aperiodisk fliselægning. Billede fra forfatternes side om resultatet.

Hvad er en fliselægning?

Fliselægninger, tilings, af hele planen, er der mange af.

Eksemplerne her er periodiske: De bringes over i sig selv ved parallelforskydning.

En mængde fliser er aperiodisk, hvis:

1. Man kan lave en fliselægning af hele planen ved kun at bruge disse fliser.
2. Denne fliselægning er aperiodisk – ingen parallelforskydning bringer den over i sig selv.
3. Man kan ikke med de samme fliser lave en periodisk fliselægning.
   

Den første mængde af fliser med den egenskab havde 20426 flisefaconer. Det var svaret på et spørgsmål i logik/datalogi, som var blevet oversat til et spørgsmål om aperiodiske fliser.

I 1974 lavede Roger Penrose, fysiker og Nobelprisvinder, et eksempel med 6 fliser:

De mest kendte Penrose-fliser er “kite and dart”

Spørgsmålet, som den nye artikel svarer på, er, om der findes et eksempel med bare én flise. Vittige tyskkyndige har kaldt der “ein Stein”-problemet – heraf Einstein.

Svaret er nu ja, og flisen kaldes Einsteins hat… Ja, nørdhumor er sommetider ikke så avanceret. På hjemmesiden for artiklen er der interaktive illustrationer, en video om, hvordan man kan lave en hel kontinuert familie af disse aperiodiske hatte, og naturligvis link til artiklen.

Aperiodicitet fra periodiske mønster i højere dimension. (Kopieret fra tidligere blogindlæg – jeg er lidt doven lige nu)

Penrosemønstre og andre aperiodiske fliselægninger/byggeklodser kan konstrueres ved “cut and project” metoden. I 1981 viste B.G. de Bruin, at alle Penrosefliselægninger, som er lavet med små og store romber, kan konstrueres udfra standardgitteret i dimension 5, altså alle punkter (x1,x2,x3,x4,x5) i  med heltallige koordinater ved

• Læg en plan ind i ,, så den ligger passende skævt – dens retningsvektorer skal have irrationale koordinater.
• Gør den lidt tykkere – gå et lille stykke ud vinkelret på begge retningsvektorer
• Projicer alle de gitterpunkter, der ligger i den optykkede plan ind på den oprindelige plan og forbind dem med kanter, hvis de var naboer i gitteret.

Det giver naturligvis et mønster i hele planen.

Hører man til dem, der ikke så let kan forestille sig to-dimensionale planer i det fem-dimensionale rum, er her et eksempel på at lave aperiodiske mønstre på en linje ved cut and project fra standardgitteret i planen.

Bemærk, hvordan der er to forskellige linjestykker, som dækker, men man kan ikke parallelforskyde og få same mønster. Det opfylder ikke betingelsen om, at man ikke kan ommøblere og lave et periodisk mønster, men som sagt er det lettere at se en linje i planen end en plan i , og princippet om, at det porjicerede mønster er aperiodisk, kan vi godt se i eksemplet med linjen.

Billederne nedenfor viser en projektion af den 5-dimensionale kube vinkelret ind på en plan, som ligger skævt – altså punkter med koordinater (0,0,0,0,0), (1,0,0,0,0), (0,1,0,0,0),…,(1,1,0,0,0) ,… etc. op til (1,1,1,1,1) – der er 32 hjørner – og kanterne imellem dem. Der er taget flere hjørner og kanter med – punkter af typen (2,0,1,0,1,0). Det er jo hele heltalsgitteret, der er i spil. Det er vigtigt, at planen ligger skævt, da punkterne ellers havner oveni hinanden. (Tænk selv over det) Her er, så vidt jeg kan se, diagonale hjørner, der lander oveni hinanden – (0,0,0,0,0) og (1,1,1,1,1).
De hvide klatter er et mønster opdaget af kemikeren Schechtman i 1982. Det er bemærkelsesværdigt ved at have rotationssymmetri af orden 10, og det er der ingen periodiske krystalstrukturer, der har (jeps, det kan man bevise). Det var den første aperiodiske krystal-struktur – og det gav Nobelprisen mange år senere.

Det første indlæg på bloggen hed Sker der noget nyt i matematik? Det gør der – der var på det tidspunkt (i 2015) 3,187,215 publikationer registreret i MathSciNet, (man skal nok være på et bibliotek eller et universitet for at have adgang) som er en database med alle de matematiske artikler og forskningsbøger, der nogensinde er publiceret, sådan cirka da. Man kan ikke læse hele artikler i MathSciNet, men titler, forfattere, tidsskrift og for langt de fleste et review af, hvad de indeholder, så man kan fritekstsøge – meget nyttigt.
Artiklen, hvor Andrew Wiles beviste Fermats sidste sætning, som man kan læse om på bloggen under Kan man skrive en børnebog om Fermats sidste sætning?, er registreret sådan her:

Jeg har ikke kopieret det review, der også er der. Det er langt og ikke let at læse, hvis man ikke er inde i branchen modulære elliptiske kurver. Der er 729 artikler, der citerer/refererer til denne artikel.

I dag er der 4,186,921 publikationer registreret. Så der er skrevet meget.
Der er en tilsvarende europæisk baseret database, Zentralblatt , som så vidt, jeg kan se, har open access. Deres ældste registreringer er fra 1868 (dengang hed det Jahrbuch für Mathematik) , hvor de har 879 artikler – MAthSciNet har 78 fra det år. I nyere tid har MathSciNet flest.
Det er artikler publiceret i visse matematiske tidsskrifter, det er bøger og det er konferencepublkationer, kaldet proceedings, hvor artiklerne er blevet fremlagt på en konference. Der er lige nu 1650 aktive tidsskrifter i MathSciNet. Det er færre end i 2015.

I 2014 blev der registreret  89642 nye artikler i tidsskrifter. I 2021 blev der registreret 120809. I perioden 2016-2021 inklusive er der kommet 668901 nye artikler i databasen. Registreringen for 2022 er ikke færdig endnu – det er derfor, jeg kun går til 2021. Det kommer altså flere og flere artikler og der er helt sikkert ingen, der har overblik over al den nye matematik.

Hvad med de gamle artikler. Bliver de ikke forældede? Det gør de som udgangspunkt ikke. Matematikken i dag bygger på ideer, metoder, resultater langt bagud i historien, og man kan ikke vide, om man skal bruge noget, der er fra 1810, som er den ældste registrering i databasen.

Matematikere forsker i et mindre område af matematikken. Når man skriver en matematisk artikel, skal den karakteriseres med emneområde(r). De mulige emnenumre finder man i Mathematics Subject Classification, MSC, (site check. Måske kan man lettere få adgang til ZentralBlatt, hvor man også bruger MSC), hvor der lige nu er ca. 6.600 numre at vælge imellem under 97 hovedområder. Der er tilsvarende emnenumre for datalogi, for statistik og sikkert også andre områder, men her holder jeg mig til matematik.

Min viden om mit matematiske område, algebraisk topologi er for nylig blevet nyttig i anvendelser i bl.a. kemi. Det nye område, Topologisk Data Analyse, har fået et nummer i MathSciNet ved en revision i 2020. Det er nu 55N31 Persistent homology and applications, topological data analysis. Og, for den statistiske del af området, 62R40 Topological data analysis. Man vil ofte sætte flere af disse numre under en artikel.

Det var en stor anerkendelse for dette nye (opstået i 1992) forskningsområde at få sin egen indgang, men det tog så også næsten 30 år… forrige opdatering var i 2010. Det er et større arbejde.

I blogposten Der er tre huller i en t-shirt lovede jeg, at vi skulle se på huller i forskellig skala. Zoomer man meget ind på en t-shirt, er der masser af huller igennem det materiale, det en strikket af, så der er tydeligvis flere svar på “hvor mange huller”.
I den tidligere blogpost gik jeg ud fra, at materialet var noget helt uden små huller, og det er det jo aldrig – ikke for en kemiker eller fysiker. Det viser sig at være vældig smart – hvis man tager det alvorligt og bruger persistent homology. Persistent kan betyde vedholdende, vedvarende eller ihærdig og her er det nok mest vedvarende, man skal tænke på.

Her er først opskriften på at komme fra atomers placering til noget med huller/loops/homologi. Tegningen nedenfor er i 2d, fordi det er lettest at tegne.
Man starter med de 12 punkter. Så lader man kugler vokse med centrum i punkterne – større og større radius. Undervejs holder vi øje med, om kuglerne mødes.

• 1. Når to kugler mødes indsættes linjestykket mellem deres centre.
  2. Når tre kugler mødes – ikke bare parvis – indsættes en trekant (hele trekanten, ikke kun dens kanter.)
  3. Når fire kugler mødes, indsættes et tetraeder – ikke kun overfladen, men hele tetraedret.

Det giver en figur bygget af punkter, kanter, trekanter, tetraedre, som i forrige blogpost

Undervejs opstår huller af dimension 1 (der er loops), de bliver fyldt ud med trekanter, når kuglerne er vokset mere. Man siger, de fødes ved en vis radius og dør ved en anden. Det holder man styr på, og tæller rigtigt – husk, der er (kun) tre huller i en t-shirt.
For hvert loop har man to tal, fødselsradius og dødsradius. Det giver et punkt (fødsel,død), som på grafen her

Man kunne finde mange andre loops undervejs, men de er talt med, som vi så med hullerne i t-shirten.

Hullet, der lever længst, A, er, når man kigger på punkterne, nok det med overbevisende hul, men i kemi vil vi gerne kende både små og store huller, altså på forskellig skala. Hvordan ser man f.-eks. forskel på glas og væske? Det er ikke let med det blotte øje. Billederne viser resultatet af simulering af glas og væske i en (stor) computer. Det er derfor, vi ved, hvor atomerne sidder:

Nedenfor har vi udregnet persistent homology og sat punkter svarende til loops ind i et koordinatsystem. Man kan godt se, der er en forskel på væske og glas i de diagrammer. Det kan kemikerne kigge nærmere på,

Vi kan sammenligne disse persistent diagrammer, som de hedder, ved for eksempel at bruge Machine Learning. Vi kan se på forskellige typer glas og vi kan selvfølgelig se på meget andet end glas – der er meget data, der kan betragtes som punkter, lige som centrum for atomerne. Det kan endda være punkter med mange koordinater.

Så kan man gå fra datapunkter -> Persistent diagrammer -> sammenligninger via Machine Learning.

Det kaldes Topologisk Data Analyse, TDA. Man bruger selvfølgelig også “huller” af højere dimension – hulrum – og laver diagrammer for, hvornår de fødes og dør.

Lige nu kigger vi efter tunneler gennem glas. Det kan man godt tænke på, som huller af dimension 1 – i den 2d-figur, jeg har lavet med voksende kugler, kunne man forestille sig, at det var en 3d-glasstruktur, hvor man kigger gennem hullerne -svarende til at kigge gennem en tunnel… hvis læseren kan se det for sig. Det viser sig at være noget mere indviklet at beskrive tunneler, så det giver mening i kemi, men så er der jo noget at tænke over. Det bliver det kun mere interessant af.

Matematikere i branchen algebraisk topologi vil sige, der er tre huller i en sædvanlig t-shirt. Andre vil nok mene, der er fire – to til ærmer, en halsåbning og et hul, hvor underkroppen stikker ud. Så hvorfor er matematikeren uenig i det?
Forklaringen på uenigheden er, at vi først skal definere, hvad et hul er, før vi tæller dem.

XKCD peger på et andet aspekt – i branchen Topologisk Data Analyse, ser vi på “huller” på forskellig “skala”, så kemikeren har også ret – det kommer vi til i en følgende blogpost – stay tuned. Men “normal person” har fat i noget, nemlig at der mangler en definition.

Lad os få t-shirten af vejen først: Der er et hul (af dimension 1) i et objekt, hvis man kan lave et loop (en lukket kurve for afficionados, se præcisionen nedenfor), som ikke kan trækkes sammen til et punkt, vel at mærke uden at den forlader objektet eller man klipper loopet over. Man må godt strække sit loop og skubbe det rundt undervejs – så trække sammen er lidt misvisende – deformere kunne man sige.

(For de filosofisk anlagte: Hvis jeg laver et hul i badebolden, kan alle loops stadig trækkes sammen, så der er ikke noget hul i en badebold med et hul i – for topologerne…. Gisp!)

Så nu ved vi, hvornår der er ét hul og hvornår der ikke er nogen. På torus er der mange andre loops, der ikke kan trækkes sammen – man kan flytte lidt på det røde eller pink på tegningen, så får man tilsyneladende et nyt – men det gælder ikke.
Så hvordan tæller man loops?

1. To loops betragtes som éns, hvis det ene kan deformeres over i det andet – ligesom vi trak et loop sammen på kuglefladen ovenfor.
2. Man kan lægge loops sammen ved at sætte dem i forlængelse af hinanden.
3. Det tæller ikke som et nyt loop, hvis man har taget to og lagt dem sammen. -Det svarer til lineær uafhængighed i lineær algebra.
   

Antallet af huller (af dimension 1) er antal loops, når man tæller som beskrevet i de tre punkter. I figuren kan man se fire loops på en (grå) t-shirt. De deformeres, så de allesammen går igennem et fælles punkt. Det er “de samme” fire loops ifølge 1) ovenfor. Nedenfor har jeg trukket t-shirten ud og lagt den fladt – ellers er det svært at se bagsiden, og der er stadig samme loops, så det er ok. Den sidste fladmaste figur viser det grønne loop trukket sammen til at følge det røde loop, derefter det blå og så det lilla. Det grønne er altså en sum af de tre andre. Derfor er der tre huller i en t-shirt.

Andre typer huller

Der er andre typer af huller – torussen ovenfor har et hulrum indeni, og det har badebolden også. Det er huller af dimension 2 – fordi der sidder noget 2-dimensionalt rundt om, ligesom hullerne i t-shirten blev fundet via (1-dimensionale) loops.

Med matematik – loops og sammentrækning

Man kan naturligvis beskrive et loop præcist med matematik: Her er X badebolden eller torussen eller noget andet, man vil undersøge, og er intervallet fra 0 til 1. skal være kontinuert.

Man kan trække/deformere en lukket kurve over en lukket kurve hvis der er en fri homotopi:

så , for alle s, og . H skal være kontinuert.

Hvordan kan jeg vide, hvordan jeg skal deformere loops? Og om det kan lade sig gøre? Hvordan kan man regne på geometrien? Det kan man bestemt heller ikke altid, men hvis man kan dele sit objekt op, kan det hjælpe.

Trekanter, tetraedre, polyedre, huller og hulrum.

Hvis man har et objekt, der er opdelt i linjestykker, trekanter, tetraedre og højeredimensionale tilsvarende objekter – simplices hedder de – så kan man regne på huller – både dem i t-shirten og dem, der er hulrum i badebolden og torussen. Der er et par kameler, der skal sluges i forhold til t-shirt-eksemplet med kurver og deformationer.

(For den indsigtsfulde læser går vi her fra homotopi til homologi – en ret heftig kamel 🐫at sluge, men hvis man ikke ved, der er en kamel, glider den lettere ned.)

• I stedet for at tillade alle mulige loops, kan man nøjes med dem, der er sammensat af linjestykker.
• I stedet for at spørge, om et loop kan deformeres til et punkt, spørger man, om det kan fyldes ud med trekanter. I så fald er dette loop 0.
• To loops er “ens”, hvis man kan fylde ud imellem dem med trekanter.

På figuren er lavet samme loops som i tegningen før, men man må kun bruge linjestykkerne – det røde er derefter forlænget med et linjestykke til spidsen af det blå; man går altså ad den kant og tilbage. Det lilla ligesådan. Det grønne er i første omgang flyttet henover en trekant; det må man godt. I den sidste tegning er det grønne flyttet henover mange trekanter og blevet til en sum af de tre andre.

Men synspunktet er nu faktisk et andet:
Rundt om en grå/skraveret trekant er et loop – via de tre kanter. Det loop er 0 – det er fyldt ud med en trekant.
Hverken det lilla, blå, røde eller grønne er nul hver for sig – ingen af dem er fyldt ud med trekanter. Men vi kan kombinere dem. Den figur, vi får ved at se på alle de grå trekanter, har en kant/rand, som er det røde plus det blå plus det grønne plus det lilla. Så den sum er nul.

rød + blå + grøn + lilla =0

Endnu en kamel: Vi holder ikke styr på, om man løber den ene eller den anden vej rundt – det gør, at ligningen ovenfor også kan skrives eksempelvis

rød = blå + grøn + lilla

rød + blå = grøn + lilla

grøn= rød+ blå + lilla

Den sidste svarer til det, vi gjorde tidligere, altså at det grønne loop er en kombination af det tre andre.

På samme måde kan man se på andre typer “huller”. Hvor et loop dannes af kanter/linjestykker, som hænger sammen med hinanden – altså ikke har nogen frithængende ender, så er et hulrum dannet af trekanter, der ikke har frithængende sider/kanter. Trekanterne på torussen nedenfor mødes to og to langs kanter. De omslutter et hulrum. (Og ja, det er voldsomt mange trekanter…). Hvis jeg fjerner en trekant (uden at fjerne dens kanter), er dens tre kanter nu frithængende og der er ikke et hulrum indeni.

Algebra og udregninger

Algebraen bag kommer via trianguleringen, som beskrives som en sammenlimning af punkter linjestykker, trekanter, tetraedre, ,etc. hvor man har styr på, hvilke punkter, der er endepunkter for hvilke linjestykker, hvilke linjestykker, der er kanter i hvilke trekanter, hvilke trekanter, der er sideflader i hvilke tetraedre etc. Sætter man det i system, kan man bruge (smart) lineær algebra til at regne på huller af forskellig dimension. Hvis man tæller huller som ovenfor – antal huller af dimension k er udregning af dimensionen af et vektorrum – så får man – hvis vi holder os til at bygge med punkter, kanter, trekanter og tetraedre, at

antal punkter – antal kanter + antal trekanter – antal tetraedre = antal sammenhængskomponenter -antal huller af dimension 1 + antal huller af dimension 2 – antal huller af dimension 3.

Det tal kaldes Eulerkarakteristikken af det objekt, man har bygget. For en kugleflade er Eulerkarakteristikken 2. Der er 1 sammenhængskomponent (alle punkter på kuglen kan forbindes til hinanden), 0 loops og dermed 0 huller af dimension 1, 1 hul af dimension 2 og 0 huller af dimension 3.

For torussen er tallet 0. Der er 1 sammenhængskomponent, 2 loops, 1 2-dimensionalt hul. Det betyder også, at de vildt mange trekanter på den triangulerede torus opfylder

Antal (hjørne)punkter – antal kanter + antal trekanter =0
Og det behøver man ikke tælle efter. Det afhænger ikke af, hvordan man har opdelt i trekanter.

I geometrikurser møder man Eulerkarakteristikken af en lukket flade som den samlede Gausskrumning.

Der bliver (heller) ikke en blogjulekalender i år. Men der er heldigvis andre, der laver den slags. De findes på mange niveauer, så vælg den, der passer dig bedst.

MATH+ i Berlin laver en julekalender, som også er en konkurrence – de skriver “The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.” og det skal jo nok passe.

Mathigon har en julekalender med matematiske udfordringer – de kalder dem puzzles.  Der er en appetitvækker hos The Guardian med udvalgte puzzles fra sidste år. Det er i Alex Bellos’ matematikklumme, som man kan følge hele året.

Sidste år havde Plus Magazine en julekalender.  Mon ikke, de laver én igen i år. Ellers kan man jo genbruge den fra sidste år. Det kan være, de har travlt med deres matematik og VM i fodbold.

The Aperiodical har tidligere haft en julekalender. Hvis de nu ikke har én i år, så kan man jo lave sig en regel om at kigge på en blogpost hver dag hos dem. De er ret gode. Hvis nogen vil prøve Mastodon, så har Christian Lawson-Perfect og Colin Wright lavet en “instance” (hvis det hedder sådan på dansk…) for flere år siden – jeg tilsluttede mig desværre ikke. Det kunne ellers være fint at være så meget på forkant. Det hedder (selvfølgelig ) Mathstodon.

Hos The Aperiodical faldt jeg over et indlæg om, hvordan AI (i dette tilfælde DALL-E mini, som nu hedder Craion) “opfatter” diverse aspekter af matematik. Jeg synes, det er jeg sjovt. Og sigende for, hvilke billeder, der findes af matematik på internettet, eftersom det er der, dette AI lærer. Jeg har bedt den om Mathematical Christmas og fik nedenstående, som er noget mere jul end matematik.

Mathematics and Christmas er julemænd og tavler…

 

 

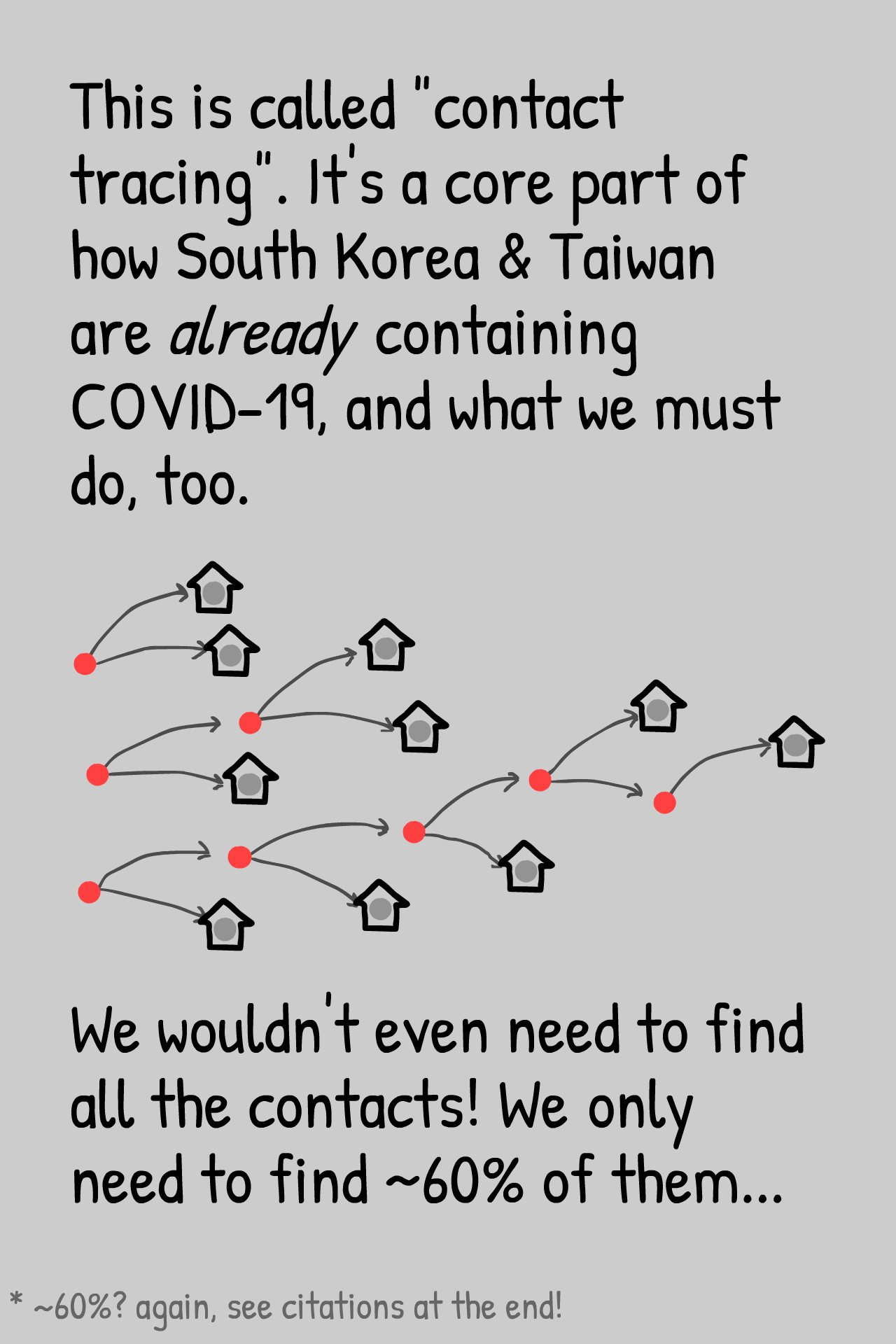
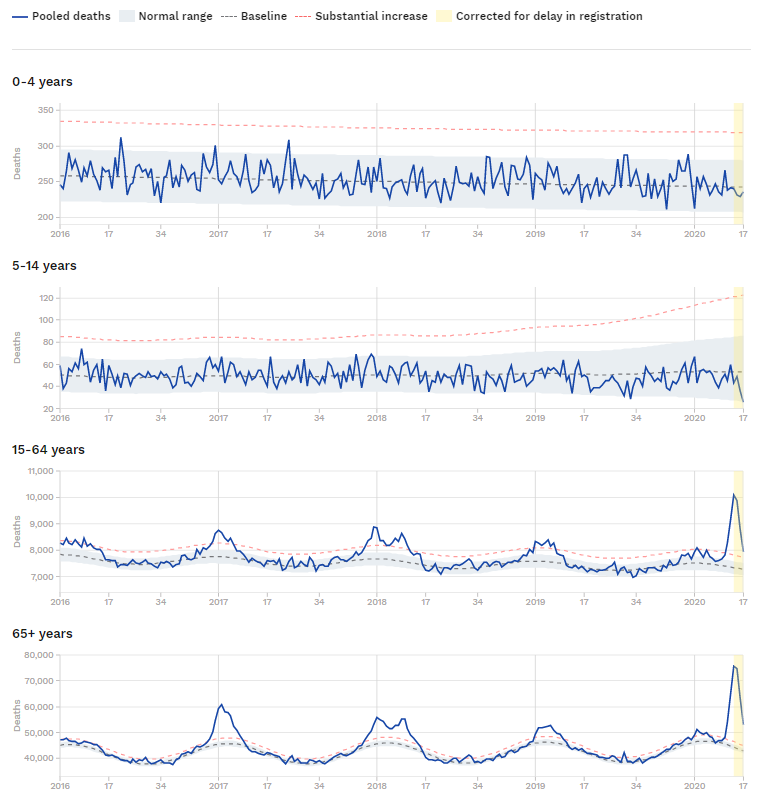
I dag, 26/3-2021 kan man læse, at SerumInstituttet ikke tæller dem, der er testet positivt ved kviktests med som smittede,men kun som muligt smittede. her kan man tage sin sølvpapirshat på og sige, de skjuler noget, men man man kan også finde brøkregnereglerne frem:

Der står: “45 procent – altså næsten hver andet – positive testsvar fra lyntest er forkert. Det er det, der kaldes falsk positive svar.”

Henrik Ullum siger i det indslag, at der udaf 1000 raske vil være 2-4, der tester positivt.

De to tal er hhv. den positivt prædiktive værdi. Hvis man tester positivt, hvad er så sandsynligheden for, at man er smittet. Den er altså 55%.

De 2-4 ud af 1000 er en beskrivelse af testens specificitet: ca. 99,7% af de raske får et korrekt svar. (Det passer ikke helt med det, man tidligere har hørt om kviktets, men det er det, Ullum er citeret for her. Tidligere har Rigshospitalet  sagt 99,5% )

De 55% afhænger af, hvor mange syge, der faktisk er, mens de 99,7% er en egenskab ved testen.

Testens sensitivitet er sandsynligheden for at teste positivt, når man faktisk er syg.

 

Lad os sige, kviktest har specificitet 99,7% og sensitivitet 70% (det er det, Rigshospitalet skriver under linket ovenfor. OBS, Jeg kender ikke de tal, Ullum bruger, så jeg gætter lidt her. Jeg tror, sensitiviteten er højere.)

Hvor kommer de positive testresultater så fra? 70% af de smittede tester positivt og 0,3% af de raske tester positivt. Vi ved også, at 55% af de positive testresultater er smittede personer. Så der er rigtig mange af de positive testresultater, der kommer fra raske personer, selvom kun 0,3% af de raske tester positivt. I kan regne videre på, hvor stor (meget lille faktisk) en andel af de testede, der så må have være smittede ved at bruge sammenhængene nedenfor. Det kaldes prævalensen og er under pandemien opgjort i incidens – antal smittede ud af 100.000.

 

I december var prævalensen (incidensen) højere, så andelen af positivve kviktest, som var fra raske, var lavere.

Lad os regne lidt:
Hvis incidensen er 20/100.000 (det kritiske niveau sidste sommer) så sker følgende:

0,3% af de 99980 raske tester positivt. Det er ca. 300 personer.
70% af de 20 tester positivt. Det er 14 personer.

Blandt de 314 positive er der nu 14 sandt positive og 300 falsk positive. Er man testet positivt, er der altså 14/314 risiko for, at man er positiv. Det er, hvis jeg kan regne, 4,5%

Hvis incidensen er 500 ser det sådan ud:
0,3% af de 99500 tester positivt. Det er ca. 298 personer – næsten lige så mange som før.
70 % af de 500 smittede tester positivt. Det er 350 personer.
Blandt de 648 personer, der tester positivt, er 350/648 altså smittet. Det er 54%.

Hvad med dem, der tester negativt?
Hvis incidensen er 20 har vi
99680 raske tester negativt.
6 smittede tester negativt.

Ud af de 99686 med negativ test, er 99680 faktisk raske. Det er 99,99 %

Hvis incidensen er 500 har vi
99202 raske tester negativt.
150 af de smittede tester negativt.
Blandt de 99352, der tester negativt, er 99202 raske. Det er 99,8%

 

Den problematik har vi haft tidligere på bloggen – Løgnedetektorer og screening for sygdom

Jeg har lavet tekster til NCUM, Nationalt Center for Udvikling af Matematikundervisning, om epidemimatematik, og herunder én om test. Den får I næsten ufordøjet her – husk, at den ikke er lagt ud af NCUM endnu. Det kommer på sitet Matematikdidaktik.dk

Test

 

Under en epidemi er det vigtigt at kunne identificere de smittede, så de kan undgå at smitte videre. Især når man kan smitte andre uden selv at have symptomer, er det vigtigt at kunne teste for sygdommen. Der testes også i mange andre tilfælde: For at give den rette diagnose og dermed den rette behandling, for at finde sygdom tidligt, så behandlingsmulighederne er bedre etc. Den matematik, der beskriver tests, er den samme uanset formålet med testen.

Om en test for en sygdom er god, afhænger af, om den finder de syge, men også af, om den ”finder de raske”, altså ikke erklærer folk syge, som ikke er det. Ekstremet er, at alle erklæres syge. Så har testen fundet alle syge, men det er naturligvis ikke en god test.

Skematisk er der for den enkelte disse muligheder:

Testresultatet er		Personen er
		Syg	Rask
Testen viser	Syg	Rigtigt	Forkert
	Rask	Forkert	Rigtigt

 

Der er to tal, der karakteriserer en test:

• Hvor stor en andel af de syge får testsvaret ”syg” (man siger, de tester positivt, hvilket kan give megen forvirring, eftersom det sjældent er positivt at være syg). Den andel kaldes sensitiviteten.
• Hvor stor en andel af de raske får testsvaret ”rask” (tester negativt). Den andel kaldes

De to tal er sjældent lige store. Begge skal helst være ret høje: Hvis sensitiviteten er lav, vil mange syge ikke blive opdaget (det er de falske negative), de kommer så ikke rettidigt i behandling og de kan måske smitte andre, når de efter testen tror, de er raske. Hvis specificiteten er lav, vil mange raske teste positivt (falske positive) og komme i behandling – det koster, og kan måske have bivirkninger. De to tal er indbyrdes afhængige: Man kan flytte grænsen for, hvornår testen betragtes som positiv – hvor meget antistof, hvor stor mængde virus,… Det flytter på både specificitet og sensitivitet.

Et andet spørgsmål kan være: Hvor stor en andel af dem, der tester positivt, er faktisk syge? Det afhænger af, hvor stor en andel af de testede, der faktisk er syge – prævalensen. Så det kan man ikke regne ud alene på basis af testens egenskaber (specificitet og sensitivitet).

Eksempel med udgangspunkt i antal:

Om en test har vi fået oplyst, at der er 100 syge og 900 raske. Og at testen viser Syg for 90 af de syge. Syg for 10 af de raske. Rask for 20 af de syge og Rask for 880 af de raske.

Hvor stor er risikoen for, at en syg person tester rask? Hvad er omvendt chancen for, at en syg tester syg.

Hvor stor er risikoen for, at en rask person tester syg? Og hvad er chancen for, at en rask tester rask?

Bemærk, at disse oplysninger ikke er normalt resultat af en test. Man ved ikke, hvem der er syge – det er derfor, man tester. Man kan forestille sig, at man prøver en ny test af på personer, der er testet med en kendt og meget troværdig test. (Det er det, vi gør, når vi tester igen med PCR)

 

Eksempel med udgangspunkt i andele: 

En test finder 80 % af de syge (har en sensitivitet på 80 %) dvs. ud af 100 syge, vil 80 teste positivt.
Den finder 90 % af de raske (har en  specificitet på 90%) dvs. ud af 100 raske, vil 90 teste negativt.

Hvis testen bruges på hele befolkningen og ca. 1% har sygdommen sker følgende for 1000 personer:

Der er 10 syge. Af dem tester 8 positivt.

Der er 990 raske. Af dem tester 99 personer positivt.

I alt er 107 testet positivt, men kun de 8 er syge. Det er 8/107, omkring 7%. Det er den positivt prædiktive værdi. Det er den, der er interessant for den enkelte: Hvis man er testet positiv, er der stadig 93% chance for, at man er rask

Hvordan med dem, der tester negativt? Dem er der 2+891=893 af. Og det er 2/893= 0,2%, der faktisk er syge. Den negativt prædiktive værdi er 99,8% (så man er ganske sikker på at være rask, hvis man er testet negativ).

 

Nu bruges samme test på 100 personer, der allerede har et eller flere symptomer. Man ved, at prævalensen da er 20%

Der er 20 syge. Af dem tester 16 positivt.

Der er 80 raske. Af dem tester 72 negativt.

I alt er 16+8=24 testet positivt og de 16 er syge. Den positivt prædiktive værdi er da 16/24, omkring 67%. Det er nu den positivt prædiktive værdi.

I alt er 4+72=76 testet negativt og de 72 er raske. Den negativt prædiktive værdi er 72/76, omkring 95%

 

Spørgsmål: Hvordan ændrer de prædiktive værdier sig generelt, hvis man kun tester den del af befolkningen, der har symptomer? (Prævalensen er større)

Mere generelt og med sandsynligheder:

 

Falsk Negative FN	Sandt Positive SP	Syge
Sandt Negative SN	Falsk Positive FP	Raske
Testet Negativt	Testet Positivt	Alle

I tabellen er resultatet af en test. Som udgangspunkt kender vi den nederste række, men egenskaber ved testen og en kendt prævalens kan give de andre celler.

Tabellen kan betragtes som andele af dem, der er testet eller som de faktiske antal. Har man de faktiske antal kan man få andele ved at dividere værdierne i alle celler med tallet ”Alle”. Omvendt: Har man andele og kender det samlede antal, kan alle andelene multipliceres med ”Alle”.

Opgave:

Nedenfor opstiller vi formler for de begreber, der blev beskrevet tidligere. Forsøg i hver tilfælde at argumentere for formlens rigtighed. Overvej, at det ikke afhænger af, om tabellen er andele eller faktiske antal.

Specificitet er 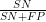, andelen af de raske, som tester negativt, altså sandsynligheden for at testen viser, man er rask, givet man er rask, det er den betingede sandsynlighed P(negativ|rask).
Sensitiviteten er 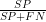  , andelen af syge, der tester positivt, igen en betinget sandsynlighed P(positiv|syg).

Specificitet og sensitivitet er egenskaber ved testen.

Prævalensen, andelen, der er syge, er .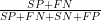

 

Den positivt prædiktive værdi er   , andelen af positivt testede, som rent faktisk er syge, sandsynligheden for at være syg, når testen viser, man er det, P(syg|positiv). Det afhænger ikke kun af testen, men også af prævalensen.
Eller, man kan se på den negativt prædiktive værdi  , andelen af negativt testede, der rent faktisk er raske P(rask|negativ).

 

Opgaver:

Udnyt Bayes’ formel til at finde sammenhænge mellem eksempelvis sandsynligheden for at være syg givet man tester positivt og sandsynligheden for at teste positivt, givet man er syg. Hvilke andre sandsynligheder indgår? Genfind prævalensen som sandsynligheden for, at en tilfældig person er syg.

 

Lige nu er der heldigvis gode nyheder om Covid19. Der er vacciner på vej! Der jubles over, hvor effektive, de er – 95% siges det om en af dem. 70% om en anden. Effektiviteten er et estimat for, hvor stor en andel af de vaccinerede, der bliver immune – i en periode. Der er usikkerhed. Måske er det i virkeligheden 73% og 92%.
Det er forskellige studier, der har givet disse effektiviteter og statistikere (Tak, Mikkel) har fortalt mig, at man ikke kan sammenligne vacciners effektivitet på tværs af studier, så det lader jeg være med. M.a.o.: Jeg regner her med tal, som hele vejen skal tages med et gran salt i statistikerforstand.

Hvor vigtig er effektiviteten mon? For den enkelte er det ret let at se, at 70% betyder, at man med en sandsynlighed på 30% ikke er beskyttet. Men der er en anden brøkregning, der kan være vigtig her.

Alle har efterhånden hørt om det famøse reproduktionstal – også kaldet kontakttallet – hvor mange smitter en smittet i gennemsnit. Og vi ved også, at det gælder om, at det kommer under 1 – så dør pandemien ud.

Kontakttallet er et gennemsnit. Der er nogen, der smitter mange, andre smitter ikke nogen. Cambridge-epidemiologerne har, før pandemien, lavet et spil, CounterPlague, hvor man kan se, hvordan det kan forløbe. For hver smittet slår man med en terning og ser fra en tabel, hvor mange, der smittes.

I Danmark er der kontakttal for hele landet, men også for mindre områder – tænk på lokale udbrud – der er kontakttallet højt i det område. Variansen betyder altså også noget for muligheden for at bremse smitten. Den kan måske vokse og dø ud et sted,  men undervejs flytte til naboområdet, som så oplever et udbrud. Det er m.a.o. kompliceret.

Hvis hver smittet i gennemsnit giver virus videre til 7 personer og vi har vaccineret 6/7 af befolkningen med en 100% effektiv vaccine, så er det kun 1 person, der bliver smittet. Vi har bragt kontakttallet ned til 1. Vi skal i det tilfælde vaccinere flere end 6/7 for at få r<1.

Hvis en smittet i gennemsnit giver virus til r personer og vaccinen er 100% effektiv, skal vi vaccinere en andel af befolkningen på .

Lige nu er kontakttallet for smitte ca. 1,2 ifølge Seruminstituttets opgørelse.
Det er i øvrigt baseret på en supersmart idé, som skal fjerne effekten af, at det er forskelligt, hvor mange der testes. Se ekspertrapporten fra 23/10

Med r=1,2 skal vi vaccinere mindst af befolkningen med en 100 % effektiv vaccine, før kontakttallet forventes at være under 1. MEN: Kontakttallet er 1,2 fordi vi lige nu overholder en lang række restriktioner og tak for det! Hvis vi nu ikke synes, det skal blive ved – selvom man vel godt kan blive ved med at vaske hænderne ordentligt – så er det et andet kontakttal, vi skal bruge. Hvad er det tal? Det kan man ikke svare helt sikkert på. Wikipedia citerer lige nu artikler for, at den grundlæggende reproduktionsrate, , er mellem 2 og 6. Kontakttallet er mindre end , men  afhænger af mange faktorer, så lad mig give nogle eksempler:

• Hvis r=2 skal der vaccineres mindst 50% af befolkningen.
• Hvis r=3 skal der vaccineres 2/3, knap 67% af befolkningen
• Hvis r=6 skal der vaccineres 5/6, godt 84% af befolkningen
• Hvis r=15 (for mæslinger er den 12-18) skal der vaccineres 14/15, godt 93%

Hvad nu, hvis vaccinen ikke er 100% effektiv? Og det er de aldrig. Tallene ovenfor drejer sig sådan set ikke om, hvor mange der skal være vaccineret, men hvor mange der skal være immune, herunder dem, der har haft sygdommen. Det er den såkaldte flokimmunitet. Hvis vi skal have 67% immune og vaccinen er 50% effektiv, er det ikke godt…

Er vaccinen 70% effektiv og vi ønsker at have 67% immune, tænker vi som følger:
Vaccinerer vi en brøkdel på x, vil vi få immune. Skal det give 2/3 (de 67%) kræver vi (man dividerer med 0,7) altså , godt 95%.

Er vaccinen 90% effektiv og vi stadig ønsker 2/3 immune, er regnestykket  godt 74%.

Med de nuværende bud på vacciner er der mange andre overvejelser – skal de køles ned til mere end en god fryser kan klare? Hvor dyre er de? Kan de produceres i store nok mængder? Og meget andet, men jeg regner med brøker her. Jeg er, som ofte skrevet her, ikke epidemiolog og nu heller ikke vaccineekspert…

Statens Serum Institut (SSI) har sammen med en ekspertgruppe udarbejdet flere rapporter med matematisk modellering af COVID-19 smittespredning og sygehusbelastning. I lang tid var modellerne (beregninger, kildekode og data) ikke åbne, men i starten af marts blev en del frigivet.

Torben Tvedebrink og jeg (Mikkel Meyer Andersen) har downloadet koden og data og kigget nærmere på modellen, der ligger til grund for ekspertgruppes rapport fra 16. april. (Bemærk at der også findes en nyere model, der ligger til grund for rapporten d. 6. maj, men her er data endnu ikke frigivet.) Vores nysgerrighed har givet anledning til blog-indlægget “Sensitivitet af ekspertgruppens COVID-19-modeller“.

I det undersøger vi hvor robust modellen er for visse antagelser (fx type af residualer og fordelingen af parameterne) og om hvor stor indflydelse data om antal indlagte på intensivafdeling har på modellens forudsigelser.

På Twitter har der også været interesse for vores blogindlæg. Bl.a. har folketingsmedlem Stinus Lindgreen (Radikale Venstre) vist interesse. Han har kæmpet for øget åbenhed for data og kildekode fra ekspertgruppen.

Vi håber at data for den nyeste model også snart frigives så vi også kan kigge nærmere på den.

Tegneserien nedenfor er lavet af Nicky Case, som også står for grafik og kodnng på den fantastiske side What happens Next? – gå først til den, hvis ikke, du har været der før. Det er sublim formidling.

Hvordan kan en kontaktopsporingsapp holde på dine hemmeligheder.

Tegneserien beskriver en konkret idé til en smitteopsporingsapp, men principperne bruges af flere og er i øvrigt ret velkendte fra feltet med kryptering, deling af hemmeligheder, at regne på/med information, man ikke kan se… hvor både matematik og datalogi er helt nødvendige. Det ser ud til, at man her bruger en lidt anden teknik  end den, vi tit hører om med primtal og andet i den talteoretiske/algebraiske boldgade.
På AAU er der også arbejde med smitteopsporing. Her er et spritnyt preprint – lavet i samarbejde mellem Institut for Matematik og Insitut for Elektroniske Systemer.

Hvor er matematikken i tegneserien (og appen): Jo, der er noget med pseudotilfældige tal. (“uniquely random gibberish”, som der står i tegneserien)  Det har jeg skrevet om før – eksempelvis her.

Alice får en engangsadgangskode (OneTimePasscode, OTP, hvis I vil Google). Bag dem ligger også pseudotilfældighed: Der skal ikke være let gennemskueligt system i, hvordan den næste kode bliver, når man har set en stribe af dem. Så ville man måske selv kunne lave sig en ved at hacke sig ind på dem, der sendes til Alice og andre.

Der bruges også et “cukoo-filter”, som er opkaldt efter gøgeunger, der vipper andre fugleunger ud. Det skal sikre, at det kun er relevant information (gøgeunger), der sendes til eksempelvis Bob i tegneserien.

Test af pseudotilfældige tal

Man skal til appen bruge en frembringer af tilfældige tal, en PRNG (PseudoRandomNumberGenerator). Den er “Pseudo” og der er altså et underliggende system i, hvordan tallene laves. Der er mange tests for, om det så er “tilfældigt nok”. Overordnet skal talene opføre sig som noget tilfældigt ville gøre. Det amerikanske NIST (National Institute for Standards and Technology) har beskrevet det og giver mange eksempler på den slags tests. Det er en statistisk test med 0-hypotesen: “Denne følge af tal er tilfældigt frembragt”. Så kan man skrue op og ned for, hvad der skal til for ikke at dumpe den test – justere den krævede p-værdi, om man vil.

Givet 20.000 tal, som enten er 0 eller 1. Læg dem sammen (ikke binært –  101 giver 2). Med 20.000 skal man få et tal mellem 9654 og  10346. Det vil rigtige tilfældige tal bestå med sandsynlighed 1-10^(-6). (Der er ca. lige mange 0 og 1 i følgen)

NIST gør følgende, som egentlig er samme ide:

For en følge  af 0’er og 1’er

lægger man sammen som følger. For hvert 1 lægges 1 til, men for hvert 0 trækkes 1 fra. Smart skrevet. Man summerer .
Eksempel: 11001010010111 giver S_obs=1+1-1-1+1-1+1-1-1+1-1+1+1+1=2.

Udregn hvor er antal bit (her 12).

Dette vil være normalfordelt med middelværdi 0 og spredning 1 for en sand tilfældig følge, så man kan undersøge, om hypotesen skal forkastes ved at udregne arealet af det, der ligger længere væk fra 0 i normalfordelingen. Det giver p-værdien. Man bruger mere end én test – se mere hos NIST eller det tyske BSI, Bundesamt für Sicherheit in der Informationstechnologie.

 

Vil man have rigtigt (sande) tilfældige tal, kan de hentes hos kvantefysikerne – henfald og bip i en Geigertæller er sandt tilfældige. Man kan hente det fra atmosfærisk støj på random.org og sikkert andre steder. Men det er dyrt, langsommeligt og dermed ikke smart til eksempelvis en smitteopsporingsapp.

En PRNG er en algoritme, som tager et input (et “seed”) og fra det producerer en streng af bits, som opfylder kriterierne ovenfor. Samme “seed” giver samme bitstreng. Men strengen skal se helt tilfældig ud – bestå de tests, NIST og andre har. Det er altså en ganske snedig algoritme.

Et eksempel på sådan en er Mersenne Twister, som bruger Mersenne primtal. Den er hurtig, men knap så sikker – man kan gætte systemet og derefter gætte næste bit. Langsommere, men mere sikker, er Blum Blum Shub, som gør som følger:

Man finder to primtal, p og q, som er meget store. Så ganger man dem og får M=pq. Nu vælges en startværdi – et “seed” x0 og udregner x2, x3,…. Talfølgen er givet ved at tage det seneste tal i rækken, xn, kvadrere det og udregne resten ved division med M.

Eksempel: p=7, q=11, så er M=77. Lad x0=15, så er x0^2= 225. Divider med 77. Resten er 225-154= 71.
Næste tal 5041-5005=36, 1296-1232=74, 5476-5467=9, 81-77=4, 16, 256-231=25

15, 71, 36,74,9,4,16,25

det ser da ret tilfældigt ud. Man bruger ikke direkte tallene fra output, men genererer en bit fra hvert af disse tal – f.eks. et 1 tal, hvis der er et ulige antal 1’er i xn skrevet binært…

Sikkerheden i Blum Blum Shub bygger bl.a. på, at det er  svært at finde p og q, selvom man måske kan finde M.

Er det så helt fuldstændig sikkert at bruge sådan en app? Se det kommer an på implementeringen. Man kan jo gøre noget andet, end man påstår. Så det er godt, man i dette tilfælde har adgang til koden bag appen. Så kan dem, der forstår det, kigge efter. Andre kan finde en, der forstår det og som man stoler på.

 

 

 

 

 

Der er gang i de matematiske modeller lige nu. Og i at forklare og misforstå dem. Her vil  jeg give eksempler på gode forklaringer leveret af andre – der er ikke grund til at lave animationer etc. igen, når gode folk allerede har leveret dem. Og så vil jeg til sidst selv forklare et lille hjørne af den matematik, der er i spil. Matematikken indgår helt fundamentalt i at forsøge at forudsige, hvad der sker, hvis… Trods de matematiske modellers begrænsninger – der er mange forudsætninger og ting med småt, når man laver en model – så vil de fleste formentlig foretrække den slags modeller fremfor at spå i kaffegrums. Vejrudsigter gælder kun et stykke tid frem – det skyldes både begrænsninger i modellen og at man ikke kender data superpræcist. Sådan er det med alle disse modeller. Finasnministeriets modeller for økonomien i år havde eksempelvis ikke inkorporeret pandemien – så de gælder nok ikke nu.

Først lige et host om de mange fortolkninger og budskaber, som florerer med enten click bait intention eller ren og skær uvidenhed/manglende omtanke. (Jo, min titel med modelbureauet er lidt click bait, så undskyld for den 🙂 )

Min yndlingsoverskrift i den retning var “Flere kvinder end mænd testes nu positive for Coronavirus”  – det var en Ritzau-nyhed og stod i rigtig mange dagblade. Den kom et par dage efter, man var begyndt at teste rigtig mange, der arbejder i sundhedsvæsenet. Er der mange kvinder i sundhedsvæsenet? Joh, det er der vist. Så det er en ikke-nyhed, omend korrekt. Det forklarede en overlæge fra Seruminstituttet da også i artiklen, men overskriften skulle vi have.

Se den slags misvisende overskrifter og artikler skyldes egentlig ikke, at man mangler matematisk viden – de fleste kan forstå, at der er en sammenhæng mellem, hvilke grupper, der testes, og hvilke grupper, man finde syge iblandt. Andre skud i tågen skyldes mere, at man tror, man forstår matematikken og derefter selv laver udregninger bagpå en konvolut (hvis nogen har en konvolut…)

Meget afhænger af, hvem man tester. Mere om det nedenfor. (Lige nu, mens jeg skriver, kan man læse, at der skal testes “tilfældige danskere” – så er man fri for den skævvridning, der er i kun at teste bestemte grupper. Til gengæld skal man overveje det, der altid er i befolkningsundersøgelser – se for eksempel The problems of a “bad” test for antibodies. Hos Winton Centre for  Risk and evidence communication. Det er  ikke den test, man vil lave i DK lige nu, men testen for virus i svælget. Der gælder de samme overvejelser naturligvis. Udover overvejelser om, hvorvidt der er skævhed i, hvem der reagerer på en meddelelse i e-boks om, at man er udvalgt til at blive testet.)

Leg med tests og falske positive, falske negative på Understanding Uncertainty

 

Gode ressourcer om matematikken og modellerne.

I fredags, 1/5, gik siden, What Happens Next    i luften. Det er en imponerende flot side, det er lavet af Marcel Salathé, Epidemiolog ved EPFL Lausanne, og Nicky Case, som har stået for “art/code” og  på  ncase.me har  matematikanimationer/illustrationer under bl.a. overskriften explorable explanations. Det er rigtig godt lavet. Vil du oversætte til dansk, er det nemt at få lov til.  Jeg har bestemt mig til, at jeg ikke har tid.
Man kan eksperimentere med modellerne uden at få “ørerne i maskinen” og kløjs i matematikken. Men man skal selvfølgelig huske, at det er  modeller. Og, som Salathé har understreget fra det første offentlige foredrag, han holdt 26/2 om epidemien: Husk at checke datoen for et indlæg. Vi bliver klogere hele tiden. En hovedpointe i “What happens Next” er, at nedlukning af samfundet har givet os en mulighed for at starte forfra med at finde smittede, deres kontakter, isolere etc. Men gå igennem hele smøren, det er virkelig oplysende. De kalder det en epidemiflysimulator. Måske skulle nogen faktisk tage sig sammen og oversætte det…

En tidligere studerende på AAU, Michael Höhle, har på sin blog skrevet om grønne og røde kurver.

Onsdag 29/4 var der et Webinar arrangeret af ECMI (European Consortium for Mathematics in Industri) under titlen math4covid19. Her stå 4-tallet nok både for “for” og “against”. Der er mange tiltag i den retning, hvor vi forsøger at samle indsatsen. Det kan ses her. Det er på et noget andet matematisk niveau end ressourcen ovenfor, i.e., en anden målgruppe. Bl.a. fortæller Uffe Høgsbro Thygesen fra DTU om de modeller, vi bruger i Danmark. Man kan notere sig, at der er meget i spil. SEIR-modeller og kontaktstrukturer, som jeg beskrev i de to foregående blogindlæg, men naturligvis statistiske modeller oveni – tidsrækker, overlevelsesanalyse, stokastisk simulering af parametrene i modellerne, generelt en række modeller og ikke kun en enkelt. Som man må forvente det.

Det sidste foredrag drejede sig om at estimere, hvor mange, der er inficeret (i gruppen I i SIR-modellen). Det vil vi nu i DK gøre ved at teste en stikprøve af befolkningen. I foredraget estimeres det udfra dødstallet. Hvorfor? Jo, især når man vil sammenligne situationen i forskellige lande, om indsatser såsom lockdown virker etc., er effekten af forskellige teststrategier helt åbenlys. Hvis vi tester mange, finder vi mange. Og omvendt. Dødstallet kan så også være påvirket af, om man i et land ikke har ressourcer til at behandle de mest syge. Så der er ikke en facitliste. Se de sidste slides for alle forudsætningerne…

Dødelighed og overdødelighed.

Dødelighed og specielt overdødelighed monitoreres i Europa på EuroMOMO. Det er vores eget SerumInstitut, der står i spidsen for det. Man skulle tro, det var nemt nok at vide, om der dør usædvanligt mange, men det er det naturligvis ikke. Man skal vide, hvor mange, der plejer at dø, hvor stor spredningen er og i øvrigt, hvilken fordeling disse tal kan forventes at følge.

Her er det samlede antal døde – på ugebasis og siden 2016.

Bemærk de mange kurver. Den fede blå er data. Den stiplede blå “basislinje”, det grå normalområde, den stiplede røde for substantial increase og så det gule område til sidst, hvor man skal korrigere for, at tallene rapporteres senere end dødsdagen – forsinket henover weekenden eksempelvis.

Hvor kommer de andre kurver fra?

I får lige en hel masse andre kurver først (der er flere, hvor de kom fra på EuroMOMO)

 

 

 

De sidste kurver er “Z-score”, som, hvis man tager det med et gran salt, siger, hvor mange standardafvigelser, man ligger væk fra middelværdien i en normalfordeling. Mere end 3, hvor den stiplede røde kurve ligger – så er man substantielt over.

Men hvad så med det, der tilsyneladende sker ved årsskiftet – man ligger altid over den stiplede kurve i december. Så er det altså ikke et gennemsnit af dødstal i december et antal år tilbage. EuroMOMO skriver selv, hvordan de gør. Det er en Poissonfordelt tidsrække med trend og desuden en sinuskurve med året som periode. Modellen er altså mindre “hakkende” end gennemsnit af data. Det er med vilje. Man vil gerne kunne se, at der, som vanligt, er influenza ved juletid, eller se, at der nu her i april tydeligvis er det udbrud – men det ved vi jo.

Man kan tænke på en situation, hvor en model er en ret linje. Og der er flere data fra hver uge – fra flere år, hvor vi har samlet data til at lave modellen udfra. Så vil man nok ikke forvente, at den rette linje går gennem gennemsnit af data i hver uge.

På den første graf kan man se, den stiplede kurve ligner en sinuskurve. Det skyldes, at man antager, at dødsfald blandt de 0-15-pårige ikke afhænger af årstiden, mens det for de over 15-årige er årstidsafhængigt – der dør flere om vinteren… så tilsammen afhænger det af årstiden, eftersom der dør flere over 15 end under. Det kan man se nedenfor, hvor døde i hele Europa er opdelt efter alder. Den grå stiplede kurve er en linje for 0-4 årige og for 5-14-årige. Den svinger for 15-64 årige og svinger mere for 65+