Jeg vil gerne fortælle jer om noget ny matematik for virus, men først skal vi have uddybet begrebet kvasikrystaller og aperiodiske fliselægninger, så dette bliver lidt en gentagelse fra sidst – dog med pænere billeder…
Klassifikation er et kerneområde i matematik. Basalt drejer det sig om, hvor mange forskellige xxx, der findes. Og her må man både have gjort klart, hvad man mener med forskellig og hvilke dyr, der hører under xxx.
Som tidligere omtalt, har vi en klassifikation af de symmetrier af planen, som
- Indeholder translation i to retninger
(vektorer) – mønsteret er bevaret, selvom man skubber det med
hvor m og n er hele tal.
- Derudover kan indeholde rotation, spejling og glidespejling.
Der er 17 forskellige symmetrier af den type. De er allesammen med på
figurerne nedenfor, som jeg har taget med, simpelthen fordi de er så flotte…. Bemærk, hvordan en grundfigur bliver flyttet rundt af symmetrierne, så det dækker hele planen. Jeg har ikke givet den helt præcise beskrivelse af hver, men I kan sikkert godt få en ide om, hvad der adskiller dem fra hinanden. At der ikke er andre, er naturligvis sværere at se.
Tilsvarende kan man klassificere symmetrier i rummet. De såkaldte krystalgrupper. Her er for eksempel NaCl eller almindeligt køkkensalt. Det har kubisk struktur, som man kan se. Og det er ret klart, hvordan man kan skubbe det rundt og fylde hele rummet op. Men der er 229 andre måder at gøre det på.
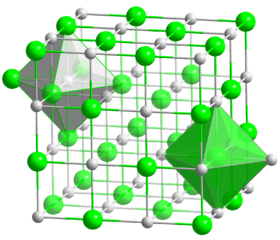
NaCl, køkkensalt. Med struktur 225 i den internationale krystalstrukturtabel. Eller Fm3m i Hermann Mauguin notation.
Kvasikrystaller, aperiodisk fliselægning
Aperiodisk fliselægning eller udfyldning af rummet har man, når man har
- Et endeligt antal flisetyper eller byggeklodser
- Et system, der giver en dækning af hele planen eller hele rummet med disse fliser/klodser sådan at der er en største periodiske delmængde (man må ikke lave en dækning med kvadratiske fliser og derefter bare dele en af fliserne i to)
- IKKE noget system, der dækker planen/rummet ved først at samle nogen af fliserne/klodserne sammen til en enkelt figur og derefter bruge denne til at dække planen/rummet.
Den sidste betingelse sikrer, at man ikke tager eksempelvis det grønne elefantmønster, vender en af elefanterne en omgang (og dermed ødelægger symmetrien) og så kalder det aperiodisk.
Penrosefliselægningen fra sidste blogpost er aperiodisk. Og mønsteret kan fortsættes til at dække hele planen.
Aperiodicitet fra periodiske mønster i højere dimension.
Penrosemønstre og andre aperiodiske fliselægninger/byggeklodser kan konstrueres ved “cut and project” metoden. I 1981 viste B.G. de Bruin, at alle Penrosefliselægninger, som er lavet med små og store romber, kan konstrueres udfra standardgitteret i dimension 5, altså alle punkter (x1,x2,x3,x4,x5) i med heltallige koordinater ved
- Læg en plan ind i
,, så den ligger passende skævt – dens retningsvektorer skal have irrationale koordinater.
- Gør den lidt tykkere – gå et lille stykke ud vinkelret på begge retningsvektorer
- Projicer alle de gitterpunkter, der ligger i den optykkede plan ind på den oprindelige plan og forbind dem med kanter, hvis de var naboer i gitteret.
Det giver naturligvis et mønster i hele planen.

Penrosemønstre fremkommet ved “cut and project” med planer parallelle med den, der giver det sædvanlige Penrosemønster. (Wikipedia Creative Commons)
Hører man til dem, der ikke så let kan forestille sig to-dimensionale planer i det fem-dimensionale rum, er her et eksempel på at lave aperiodiske mønstre på en linje ved cut and project fra standardgitteret i planen.
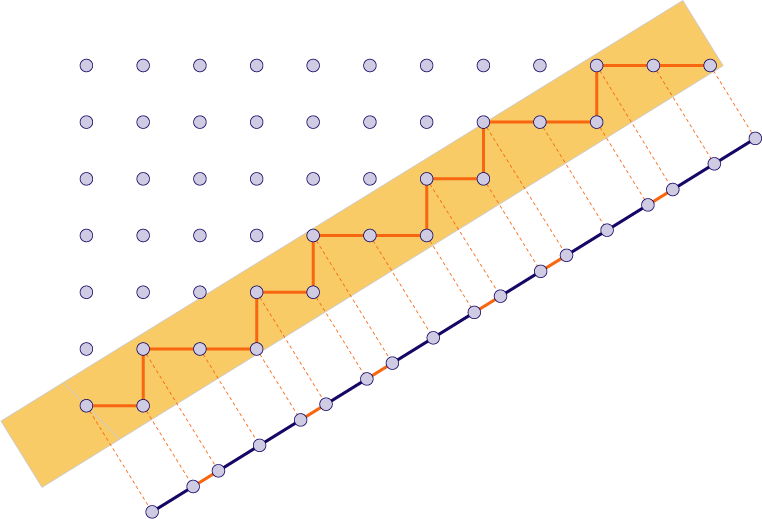
Fra regulært gitter i planen til aperiodisk mønster på linjen. Fra
1D quasicrystals by Fibonacci substitution and lattice projection
Wolfram Community.
Bemærk, hvordan der er to forskellige linjestykker, som dækker, men man kan ikke parallelforskyde og få same mønster. Det opfylder ikke betingelsen om, at man ikke kan ommøblere og lave et periodisk mønster, men som sagt er det lettere at se en linje i planen end en plan i
Billederne nedenfor viser en projektion af den 5-dimensionale kube vinkelret ind på en plan, som ligger skævt – altså punkter med koordinater (0,0,0,0,0), (1,0,0,0,0), (0,1,0,0,0),…,(1,1,0,0,0) ,… etc. op til (1,1,1,1,1) – der er 32 hjørner – og kanterne imellem dem. Der er taget flere hjørner og kanter med – punkter af typen (2,0,1,0,1,0). Det er jo hele heltalsgitteret, der er i spil. Det er vigtigt, at planen ligger skævt, da punkterne ellers havner oveni hinanden. (Tænk selv over det) Her er, så vidt jeg kan se, diagonale hjørner, der lander oveni hinanden – (0,0,0,0,0) og (1,1,1,1,1).

5-kubens hjørner og kanter og andre punkter fra det kubiske gitter i dimension 5 er projiceret ind på en plan. Lagt oveni det quasikrystal, Schechtman opdagede. (Wikimedia commons)
Morale: Man kan forstå kvasikrystaller ved at betragte periodiske mønstre i højere dimension. Husk det, når vi ses igen på bloggen til historien om, hvad det mon har med virus at gøre. Cliffhanger!

















