Ignacio Cascudo er adjunkt på instituttet her har skrevet et rigtig godt blogindlæg om, hvordan man kan ræsonnere om og regne på/med information, man ikke kan “se”. Jeg har ikke oversat det – mon ikke I kan klare at læse det på engelsk?
How to compute on information you don’t see.
Information security, and in particular cryptography, is a very popular topic nowadays. People are concerned about the privacy of their sensitive information, such as their economic situation, health, or other issues.
It is fair to say that, when we speak about cryptography, what comes to mind to most people is the subject of encryption: how to transmit a message to some other person so that if someone intercept that message, he/she will not be able to read it; you may also know about another cryptographic topic: digital signatures, which allow to prove (authenticate) that certain person is the author of a message and that it has not been modified after being signed and sent.
But cryptography also includes the study of other problems that you may not be aware of; and yet, they are really surprising, and have very important applications, which are becoming more and more popular.
-Do you know for example that using cryptographic tools you can have two parties find out who of the two is richer, or older, or heavier without any of them having to reveal (to the other person or to anybody else) his/her actual wealth, or age, or weight? This can be used for “benchmarking”, where two or more companies can compare these results and find out their weaker points with respect to the competition, without needing to reveal precisely how well or bad they are doing.
-Or that you can run an auction among several people, where everyone of them want to bid some amount for an item and determine who wins the bid without needing to reveal the bids of the losers? This can be used for automatic bidding for ads in the internet. Another scenario where this was used in a pioneer work, carried out in Denmark by researchers of Aarhus University, is the trading of sugar beet prices between the company Danisco and farmers.
-Or that you can run a voting with several voters so that none of them has to ever reveal their vote to anybody, yet at the end of the day, all of them know exactly the result of the voting? And you don’t need ballots for this, in principle you could do it by having each pair of voters exchange messages with each other privately.
These kind of problems is what the subject of secure multiparty computation is concerned with. Secure multiparty computation deals with the scenario where two or more parties want to jointly make some calculation involving private data held by some of them, but without actually revealing this data, they only want to reveal the outcome of the computation.
Since the spectrum of applications is very broad, different solutions and techniques are used for the different scenarios.
Voting
A simplified example of a multiparty computation scenario, where we can show an easy solution, is the following: imagine Alice, Bob and Charlie want to compute the result of a voting, where there are two possible votes (yes or no) and we want to count the number of yes votes. So if we assign number 1 to ‘yes’ and number 0 to ‘no’, we just need to compute the sum of what Alice, Bob and Charlie vote. But now, how can this be computed without having Alice, Bob or Charlie communicate their votes to anybody? Here is a sequence of steps (what is usually called “a protocol”) that can accomplish this goal:
- Each party selects three 1-digit numbers such that the sum of these numbers has his/her vote as its last digit. For example if Alice wants to vote yes, she could choose the numbers 2,4 and 5 since 2+4+5=11, and the last digit of 11 is a 1 (which means yes). She could also choose 7,7,7 (the numbers do not need to be different), since 7+7+7=21, or 0,0,1, since 0+0+1=1.
If she voted no, she could have chosen for example 6,5,9 since 6+5+9=20.
Simultaneously, Bob and Charlie do the same with their votes they have. - Each party takes the three numbers he/she has generated in step 1., and sends a different one to each other party (including keeping one for him/herself).
So, if for example Alice has chosen (2,4,5), she sends the value 4 to Bob, 5 to Charlie and keeps the value 2 for herself. - In the next step, each of the players sum the elements he/she has received (including the one he/she kept for him/herself).
- Finally each of the players announces publicly the last digit of the sum each one has computed. The results are in turn summed and the last digit of the sum is the final result of the voting.
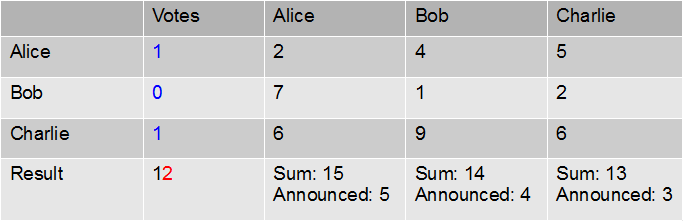
The table below represents a voting situation: the votes are in blue. The entry corresponding to e.g. Alice row and Bob column is the number Alice has sent to Bob (4, in this example); the entry corresponding to Alice row and column is the number she has generated and kept for herself (2 in this case).
The last values in each column correspond to the sum of the values received by each player (e.g. 15=2+7+6 for Alice), of which each announces publicly the last digit. The sum of these announced digits (which is 12 in this example) is therefore a public value, of which the last digit 2, is the number of yes votes.
This protocol always gives the correct sum of the votes and, almost magically, the vote is private in the sense that the vote of each player remains hidden from the others.
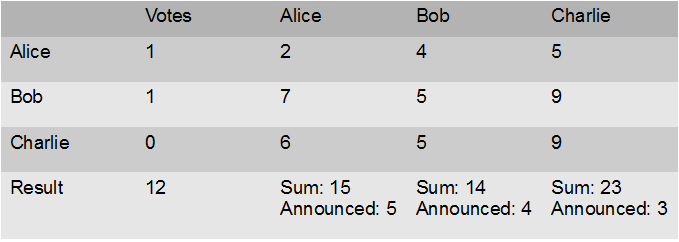
At this point you may complain: “but, that cannot be true, because consider Bob; he voted no (0) and the result was 2 yes votes, so he does know the votes from the other players have to be yes”. This is true; however, it is unavoidable: since the outcome has to be public, no matter how we do the voting (by a multiparty computation protocol, with the help of some trusted mediator or in any other possible solution) Bob would know that Alice and Charlie voted yes. What multiparty computation protocols have to deal with, is to avoid that other information is leaked: for example, since Alice has voted yes, and the was result was 2 yes votes, she should have no information about whether the other yes-voter was Bob or Charlie.
But how could one even be sure about this?. The key is that one can imagine this alternative situation:
The information seen by Alice (her row and column, the announced values and the vote outcome) is exactly the same in this case as in the one above, yet in the case above it was Bob who voted yes, while in the situation below the yes-voter was Charlie. For Alice, it is as solving a Sudoku that has two solutions and each of the solutions leads to a different guess about who is the other yes-voter.
But what happens if a player tries to cheat, sending wrong information (for example vote “2”)? Or if a player refuses to continue with the protocol at some point? And how do you compute functions more complicated than sums? Many different tools involving different mathematics are needed to address all these problems, with fancy names such as oblivious transfer, commitment schemes, secret sharing or zero knowledge proofs (cryptographers are good at baptising their tools). One interesting tool from the mathematics point of view is secret sharing.
Secret sharing
At the beginning of the protocol above, Alice, Bob and Charlie distribute their votes among each other, in such a way that no single person knows the vote of anyone else.
This technique of distributing information is called secret sharing, and can be used for other goals too: for example, if you want to store some important information (a “secret”) but you are afraid to leave it in one place, where it could be potentially accessed by someone you don’t trust; in that case, you could think of distributing the information across several locations (e.g. several hard disks). Secret sharing even allows to do it in such a way that you can share a secret among, say, 4 computers so that if the information stored in 2 of them is accessed, the secret is kept completely hidden; but on the other hand you can recover the secret if you can access any 3 out of the 4 computers (so if one of them crashes you still don’t lose the secret).
The most popular secret sharing scheme was invented by Adi Shamir (the same Shamir that invented the RSA cryptosystem together with Ron Rivest and Leonard Adleman) and it uses properties of evaluations of polynomials. It is in fact based on the same ideas as another tool of discrete mathematics known as “Reed-Solomon error correcting code”, used for the reliable and efficient transmission of information through channels with noise.
The idea is that if you are given a number of evaluations of a polynomial (for example you know that f(3)=9, f(2)=5 and f(1)=3) there is exactly one polynomial of small degree that satisfies these evaluations. “Low degree” means “less than the number of evaluations”. So in the case above, since you are given 3 evaluations, there is one possible polynomial of degree at most 2 that satisfies the conditions, which is in fact x²-x+3. One can reconstruct this polynomial using so-called Lagrange interpolation.
This is still valid if, instead of using real numbers, one works over another field, and in the case of secret sharing calculations are usually performed over finite fields (which were already explained in Turingprisen til Diffie og Hellman on the blog here.)
In Shamir’s secret sharing scheme each of the players is given the evaluation in a different point of a hidden polynomial of degree at most t. The secret is actually the evaluation of the polynomial in another different point, say for example, the point 0.
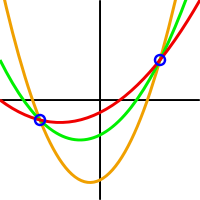
Now if t+1 participants meet and pool together the shares they have receive, they together know t+1 different evaluations of f, and then they can determine the polynomial, since we know it has degree at most t. But t players together will be missing one evaluation point, and in fact for every element of the field there will be exactly one polynomial consistent with the information they know and that yields this element as secret.
This picture shows several polynomials of degree 2 consistent with the same 2 evaluations. If we have taken t=2 in the explanation above, the set of 2 players who know these 2 evaluations, will not be able to know the secret, since each of the possible polynomials of degree at most 2 leads to a different evaluation in 0. Source:wikipedia