Hvor mange forskellige trekanter findes der?

Dumt spørgsmål. Der er (mindst) to problemer: Hvad betyder forskellige? Og næsten uanset, hvad det betyder, så er der nok uendelig mange. Hvilket igen kan betyde flere ting, for vi har forskellige slags uendelig….

Det er typisk i matematik: Spørgsmålene skal justeres, før vi kan få et meningsfuldt svar.

I løbet af sommeren har der været forskelige “svar” på lignende spørgsmål: Hvor mange billardborde findes der med visse egenskaber (sætter man en kugle til at rulle, vil den enten i det lange løb komme vilkårligt tæt på alle punkter på billardbordet eller gentage den samme bane igen og igen) – se Quanta Magazine .

Hvis en femkant skal kunne bruges som eneste flise i en fliselægning, som dækker hele planen, hvad kan man så sige om den femkant? Svar: Der er 15 forskellige muligheder.

Tilbage til trekanterne. I skolen er to trekanter ens, hvis de er kongruente. To figurer er kongruente, hvis man kan få den ene til at ligge præcis oveni den anden ved at parallelforskyde og dreje – og sommetider tillader man også spejling.

Paralleforskydning, drejning og spejling bevarer vinkler, længder og arealer, så vi har følgende

Hvis to trekanter er kongruente, så er deres vinkler parvis ens.
Hvis to trekanter er kongruente, så er deres sidelængder parvis ens.
Hvis to trekanter er kongruente, så har de samme areal.

I geometri i gymnasiet eller grundskolen har de fleste set eksempler på argumenter “den anden vej”:

Hvis to trekanter har parvis ens sidelængder, så er de kongruente.
Hvis en vinkel og de to hosliggende sider er lige store, er de kongruente.
Hvis en side og de to hosliggende vinkler er lige store, er de kongruente.

Illustrationen er fra Wikipedia:

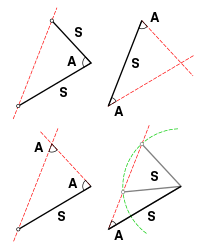
Lad os stille spørgsmålet igen: Hvor mange forskellige trekanter er der, når kongruente trekanter anses for ens?

Igen er svaret uendelig mange, men der er et bedre svar, nemlig en klassifikation. Ovenfor genkaldte vi resultatet fra gymnasiet: Hvis to trekanter har parvis ens sidelængde, så er de kongruente.

M er mængden af alle trekanter. Den opdeler vi i kongruensklasser – en kongruensklasse K er en delmængde af M, hvori alle trekanter er kongruente og sådan at trekanter udenfor K ikke er kongruente med trekanter i K. Det giver en opdeling af M i delmængder, som ikke har noget fælles med hinanden – disjunkte delmængder. (Man kan vise, kongruens er en ækvivalensrelation og udlede det derfra. ) Notationen [T] står for den kongruensklasse, som indeholder trekanten T, altså alle de trekanter, som er kongruente med T.

Definer en funktion F:M -> $\mathbb{R}^3$ ved $F(T)= (a,b,c)$ , hvor a,b,c er sidelængderne for T og $a\leq b\leq c$ .

Et par observationer:

$F(T_1)=F(T_2)$ hvis og kun hvis $T_1$ er kongruent med $T_2$ . Så vi kan definere

G: {kongruensklasser af trekanter } -> $\mathbb{R}^3$ ved $G([T])=F(T)$ .

Vi ville gerne kunne sige: Der findes præcis en kongruensklasse for enhver vektor $(x,y,z)\in \mathbb{R}^3$ med $0 <x\leq y \leq z$ – det ville give en klassifikation; en direkte oversættelse fra trekanter til bestemte vektorer i rummet og tilbage igen. Altså en invers til funktionen G.

Men det er helt sikkert forkert: $(1,2,4)$ er ikke sidelængderne i en trekant. – Den sidste sidelængde er “for lang”. Det er ikke alle sådanne (x,y,z), som er i billedmængden for F.

Trekantsuligheder

I en trekant opfylder sidelængderne (a,b,c) følgende uligheder:

$a+b > c$ .
$b +c > a$ .
$a+c > b$ .

Når vi navngiver, så $a\leq b \leq c$ , er ligning 2 allerede opfyldt. Ligning 3 kan udledes:
$c+a\geq b+a >b$ , så nu er spørgsmålet:

Kan vi altid finde en trekant med sidelængder $(a,b,c)$ , hvis bare $(a,b,c)$ opfylder $0<a\leq b \leq c$ og $a+b > c$ ?

Det kan vi. Det kan man f.eks. se som følger:

Cirklen med centrum i (0,0) og radius a skærer cirklen med centrum i (c,0) med radius b i et punkt P, som ikke ligger på x-aksen. trekanten med hjørner (0,0), (c,0) og P har sidelængder som ønsket. Punktet P=(x,y) kan findes som skæringspunkt mellem de to cirkler, altså som løsning til et ligningssystem:

Ligningen for cirkel 1 $x^2+y^2=b^2$ og for cirkel 2 $(x-c)^2+y^2=a^2$ . Det giver

$x=\frac{b^2+c^2-a^2}{2c}$ og $y=\pm\sqrt{b^2-\frac{(b^2+c^2-a^2)^2}{4c^2}}$ . Der er to muligheder – cirklerne skærer hinanden ovenfor og nedenfor linjestykket (0,0) – (c,0).

Eller man kan bruge, at cirkler er kontinuerte kurver og se, at de passerer x-aksen i hhv. -b, b og c-a og c+a. Da c-a < b må de to kurver skære hinanden for at nå til yderpunkterne (-b,0) og (c+a,0).

Konklusion:

Der findes præcis en kongruensklasse af trekanter for hvert $(a,b,c)\in \mathbb{R}^3$ , som opfylder $0<a\leq b \leq c$ og $a+b > c$ .

Det er et klassifikationsresultat. Det udnytter, at sidelængder er invariante under de flytninger, vi tillader i kongruensrelationen. Og omvendt, at trekanter med samme sidelængder er kongruente. Desuden skulle vi have skåret billedmængden for F til. Her kan vi endda konstruere en trekant med de givne sidelængder. Det kan man ikke altid i klassifikationsresultater – ofte ved man blot, der findes en.

Andre spørgsmål, man kan stille er.

Hvis afstanden fra (a,b,c) til (x,y,z) er lille, kan man så sige noget om afstanden mellem de tilsvarende kongruensklasser af trekanter? (Ja, hvis man definerer afstand mellem trekanter passende.)
Hvad kan man sige om 4-kanter?
Hvis trekanter er ens, når de er similære (den ene er kongruent til en skalering af den anden), kan man så klassificere dem? (Ja. Skaler, så den længste side er 1 – det må man godt, da similær=ens. der er nu en similaritetsklasse for hvert par (a,b) med $0<a\leq b\leq 1$ og $a+b\geq 1$ . Den mængde kan I tegne i planen. Det bliver en trekant med hjørner (0,1), (1,1) og (1/2,1/2). )
og meget mere….

Klassifikation er en matematisk grunddisciplin a la biologernes kortlægning af dyr og planter. Det er nysgerrighedsdrevet, men ofte også meget praktisk anvendeligt. Klassifikation af krystalstrukturer er matematik, men grundlæggende for kemi.