Lisbeth Fajstrup spurgte mig tidligere på året, om jeg kunne skrive et blogindlæg, som svarede på de to følgende spørgsmål: (1) hvorfor skal -værdier være mindre end
og (2) hvordan flere sammenligninger har indflydelse på
-værdien (også kaldt multiple testing problemet). Det er to gode spørgsmål, og i skrivende stund, mens vi er kommet godt ind i det nye år, har jeg endelig tid (taget mig sammen til at finde tiden) til at svare på de to spørgmål. Inden jeg gør dette, for at sikre vi alle er på samme side, introducerer jeg kort
-værdi konceptet, med den sædvanlige tunge definition og et kort eksempel. Hvis læser allerede ved hvad
-værdier er, kan dette afsnit nemt hoppes over. Hvis læser aldrig har hørt om
-værdier før og ønsker en mere fuldstændig introduktion, så se for eksempel the American Statistical Association’s artikel fra 2016.
Kort introduktion til p-værdier
Helt generelt defineres -værdien som:
Sandsynligheden for at observere en teststørrelse der er ligeså eller mere ekstrem, end hvad der allerede er observeret, givet at nulhypotesen er sand.
For at illustrere, hvordan dette skal forståes, lad os tage et eksempel:
Lad os sige, at vi vil undersøge om befolkningen bakker op om Formel 1 ræs i København. Vores nul hypotese er at befolkningen hverken er for eller imod, altså at opbakningen er fifty-fifty. Alternativet er, at opbakningen er mindre eller større end , da vi ikke forud for undersøgelsen har indsamlet noget information.
Vi går ud i landet og spørger seks tilfældige personer. Det viser sig at alle seks personer støtter op om forslaget. Under nulhypotesen er sandsynligheden for at se seks observationer ‘imod‘ forslaget:
og da vi ikke er forudindtagede, så er seks individer ‘for‘ forslaget lige så ekstrem en observation. (Og der kan ikke være observationer, som er mere ekstreme.) Dette medfører en -værdi på:
Er dette nok til at forkaste nulhypotesen? Hvis vi skal spørge det hav af lærebøger der bruges i statistik undervisning, vil de sige, at nulhypotesen forkastes så snart -værdien er mindre end
. Perfekt! Alt er som det være, verden er flad placeret på ryggen af en skildpadde der står på ryggen af en større skildpadde.
Den udregnede -værdi fortæller os ikke meget andet end, hvad vi kan læse af definitionen: Hvis nulhypotesen er sand, så er sandsynligheden for at trække en ny stikprøve, hvor andelen er mere ekstrem end den vi så ovenfor, lige over
. Er tre procent nok til at vi ikke tror det er et tilfælde?
Hvis vi sætter en beslutningsgrænse (signifikansniveau) kan vi begå to typer af fejl:
- Type I: Nulhypotesen forkastes selvom den er sand.
- Type II: Nulhypotesen forkastes ikke selvom den er falsk.
Sætter vi beslutningsgrænsen i vores eksempel ovenfor til, at alle seks er ‘for‘ eller alle seks er ‘imod‘, før vi forkaster nulhypotesen, så er sandsynligheden for at begå en Type I fejl (
-værdien set ovenfor).
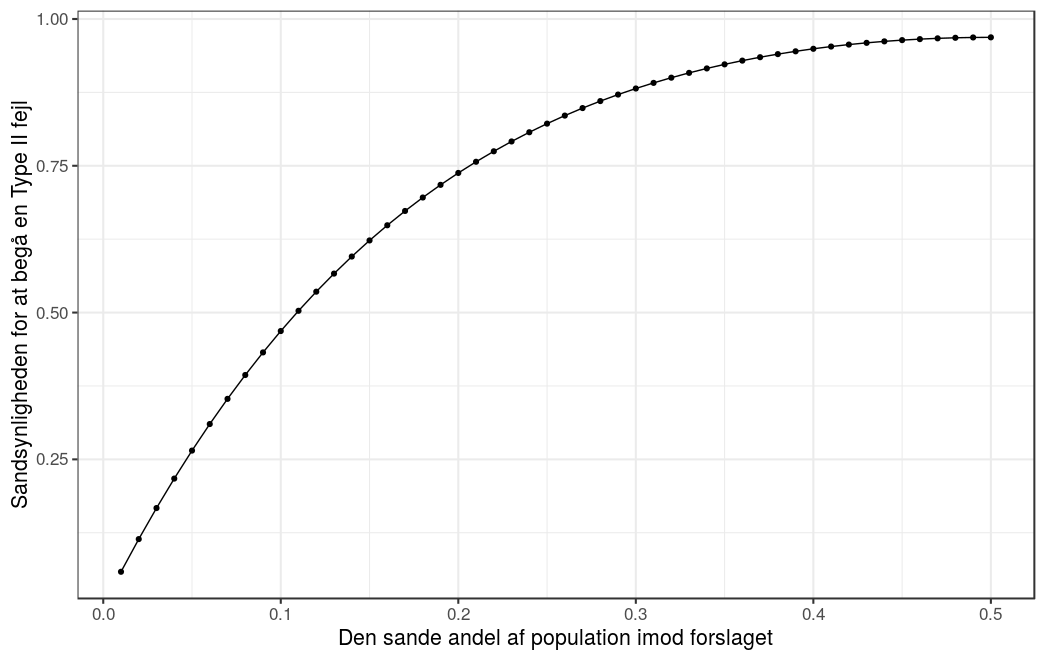
Sandsynligheden for at vi begår en Type II fejl vil afhænge af signifikansniveauet og den sande andel af populationen som er ‘imod‘ (eller ‘for‘) Formel 1 løb i København. Lad os se hvad der sker, når vi antager at sande andel af populationen som er ‘imod‘ er (altså er andelen, der er ‘for‘
). Vi antager som ovenfor, at vi kun forkaster nulhypotesen når alle seks er ‘for‘ eller alle seks er ‘imod‘, givet dette signifikansniveau er sandsynligheden for at se seks observationer ‘imod‘ forslaget:
og sandsynligheden for at se seks observationer ‘for‘ er:
Dette giver en sandsynlighed for at begå en Type II fejl på:
hvor kaldes for den statistiske styrke af testen, og fortolkes som sandsynligheden for forkaste nulhypotesen, givet at den faktisk er falsk.
Det vil sige, at hvis den sande andel af populationen som er ‘imod‘ er , vil nulhypotesen ikke blive forkastet i knap
af tilfældende, selvom den er falsk og den sande andel ‘imod‘ forslaget endda ligger meget langt fra nulhypotesen,
. Vi kan gøre det samme for enhver andel og resultatet kan ses i figuren nedenfor. Bemærk: figuren kun viser den første halvdel, da figuren er symmetrisk omkring 0.5.
Grunden til den høje sandsynlighed for Type II fejl i denne sammenhæng er valget af signifikansniveau og, hovedsageligt, det lave antal af observationer. Dette betyder at når vi designer et studie, (planlægger, hvor mange og hvem, vi skal spørge/teste/…,) så prøver vi at finde en balance mellem tre størrelser: signifikansniveauet, styrken, og stikprøve størrelsen.
Hvorfor skal p-værdier være mindre end 5%, før de kaldes statistisk signifikante?
Ikke et specielt tilfredsstillende svar, men det er sandheden. Vi lærer vore elever og studerende det, fordi vi selv fik det at vide af vore undervisere. Dette svar, kombineret med at flere tidsskrifter i de seneste år har valgt at direkte afvise artikler der indeholder -værdier, gjorde at ‘the American Statistical Association’ (ASA) i 2016 publiserede en artikel der redegjorde for, hvad
-værdier er og hvordan de bør fortolkes (en udmelding der fik, blandet andet, danske statistikere Claus Thorn Ekstrøm og Per Bruun Brockhoff, til at stikke hånden i vejret og proklamere: “Intet nyt under solen”). Det svarer dog ikke rigtigt på spørgsmålet: Hvorfor lige præcis
?
Det simple svar er: fordi R. A. Fisher skrev det og hans ord lov. Fisher er en af de mest anerkendte statistikere, og bliver generelt betragtet som en af fædrene til moderne statistik. Et eksempel på Fishers brug af signifikansniveauet, kan ses i hans artikel fra 1926:
If one in twenty does not seem high enough odds, we may, if we prefer it, draw the line at one in fifty (the 2 per cent point), or one in a hundred (the 1 per cent point). Personally, the writer prefers to set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.
Altså giver Fisher en følge af mulige signifikansniveauer efterfulgt af hans foretrukne niveau på . Lignende argument findes i hans bog ‘Statistical Methods for Research Workers‘ (1925), dog præsenteret ved standardafvigelser (for en normalfordelt teststørrelse svarer et signifikansniveu på
til knap 2 standard afvigelser). Ydermere, indeholdt bogen tabeller til opslag af fraktiler af (bestemte) sandsynlighedsfordelinger, som indeholdte:
,
,
,
,
,….
Det heller ikke så vigtigt at signifikansniveauet lige præcist er , det er størrelsesordenen som er vigtig; det gør ikke den store forskel om signifikansniveauet er
,
, eller
. Men denne størrelsesorden giver, i de fleste tilfælde, en god balance mellem den statistiske styrke og stikprøve størrelsen. Altså kan vi med et signifikansniveau omkring
opnå en høj styrke uden at skulle indsamle en fuldstændig ekstrem stor stikprøve.
Hvorfor lærer vi så stadig vore elever og studerende, at signifikansniveauet bør være ? Som jeg ser det er der tre grunde:
- Det leder, i de fleste tilfælde, til en god balance mellem andelen af Type I fejl, Type II fejl og størrelsen af stikprøven.
- Det gør det nemmere at sammenligne studier, hvis alle bruger det samme signifikansniveau og samme styrke.
- Det er nemmere at lære et stort antal elever en ‘kageopskrift’, end at få dem til at tage stilling til den andel af Type I og II fejl, de vil tillade i deres analyse.
Multiple testing problemet
Problemet opstår, når flere hypoteser testes på samme tid. Jo flere hypoteser der testes på samme tid, jo større er sandsynligheden for, at der opstår en fejl. Lad os i det følgende antage at andelen af acceptable Type I fejl er sat til .
Lad os eksempelvis sige, at vi i stedet for at teste et nyfundent stof direkte for dens effekt på sygdommen
, derimod tester det for effekten på 100 forskellig symptomer. Ydermere, antag at nulhypotesen er sand i alle 100 tilfælde (altså at der ingen effekt er). Dette vil medføre et forventet antal Type I fejl på 5 (
). Hvis de 100 hypotesetest, vi foretager, kan antages at være uafhængige, giver dette en sandsynlighed på
for at se mindst en Type I fejl, (hvor vi altså konkluderer, at stoffet virker på mindst et af symptomerne) da:
.
Sandsynligheden for mindst en Type I fejl, kaldes også ‘the familywise error rate‘ (FWER). Et oplagt spørgsmål er: hvordan kan vi sikrer at FWER er mindre end den acceptable andel af Type I fejl? Der har gennem årene været en del bud på løsninger til dette problem. Vi kaster et kort blik på den simpleste og mest anvendte procedure, Bonferroni korrektionen.
Lad være
-værdien for hypotese
, så afvises
, i følge Bonferroni, hvis
hvor er den acceptable andel af Type I fejl og
er det totale antal af hypoteser. I vores eksempel er
og
. Beviset for at Bonferroni korrektionen sikre FWER
er som følger:
hvor første ulighed holder ved Booles ulighed, der siger at:
Bonferroni korrektionen er en særdeles konservativ metode, hvis der laves mange hypotese test eller -værdierne er positivt korrelerede. Dette betyder at korrektionen foregår på bekostning af et større antal Type II fejl.
I de senere år, er dette blevet et problem ifm. ‘genome-wide association studies‘ (GWAS). Her testes forskellen i individers DNA baser (de byggesten vore kromosomer består af) for deres indflydelse på en sygdom eller et fænotypisk træk (så som hårfarve). Applikationer som denne, har ført til en række alternativer til Bonferroni korrektionen. Den mest anvendte her i blandt er ‘false discovery rate‘ (FDR), som blev formelt beskrevet af Yoav Benjamini og Yosef Hochberg i 1995, altså en forholdsvis ny metode i denne sammenhæng. Mere information kan findes på wikipedia siderne: ‘Multiple comparison problem‘, ‘Bonferroni correction‘, ‘False discovery rate‘, og ‘Genome-wide association study‘.