Billedet viser en ny togstation i Cambridge UK. Mønsteret påstås, ifølge The Aperiodical at være John H. Conways “Game of Life”, som han arbejdede med, da han var i Cambridge. (Det skriver arkitektfirmaet her )

Det er ikke helt korrekt, men der er noget om snakken. Mønsteret er en 1-dimensional cellulær automat, mens Game of Life er 2-dimensional.

Cellulære automater.

En cellulær automat består af

1. Et gitter/ grid eksemplevis i planen: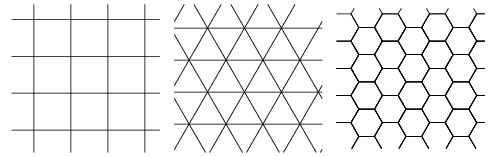Fra Mathworld
2. En farvning af nogen af felterne – lad os holde os til sort/hvid, farvet/ikke farvet
3. En regel for, hvordan farverne skifter når tiden går (den går i hop) – afhængigt af nabocellernes farver. Her skal man også definere, hvilke felter, der er naboerne.

Eksempler på naboer:

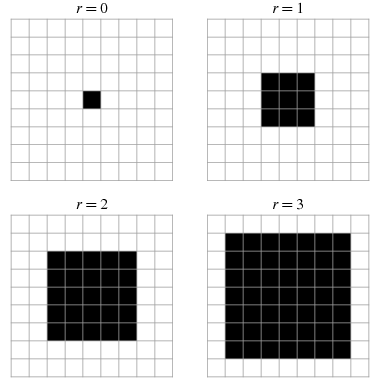Moore-nabolag (Fra Mathworld).

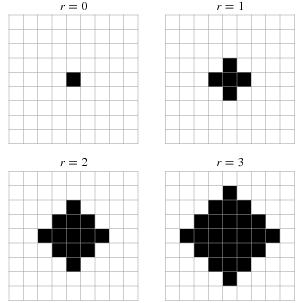Von Neumann nabolag (fra Mathworld).

 

Eksempel: Game of Life.

Gitteret er det første ovenfor. Det dækker hele planen.

Naboerne til en celle er Moore-nabolaget med r=1.

Regler:

Kald en sort celle “i live” og en hvid “død”. (Det er mere dramatisk.) Hver celle har 8 naboer.
1) Hvis en levende celle har to eller tre levende naboer, forbliver den i live. (Har den flere end tre, dør den af overbefolkning; har den kun 1, dør den af ensomhed.)
2) En død celle med præcis tre levende naboer kommer til live.

Der skiftes farve på alle celler på en gang.

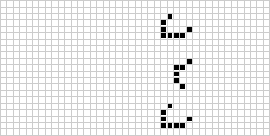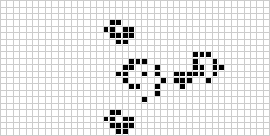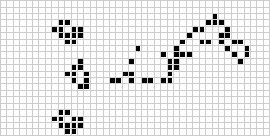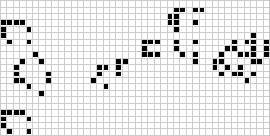 Her er et Game of Life, som gentager sig selv. (fra Mathworld.)

En-dimensionale cellulære automater:

Her er der et grid på linjen. Nabolaget er cellen selv og den til højre og til venstre for den. Udviklingen illustreres med en tidsakse, så alle generationer er med i illustrationen.

Derer 8 forskellige konfigurationer for en celle og dens naboer – hvis vi holder os til to tilstande. 111, 110, 101, 100, 011, 010, 001, 000

For hver af de 8 kan man bestemme, hvad centercellen skal være i næste skridt. Det giver muligheder.

Eksempel: 

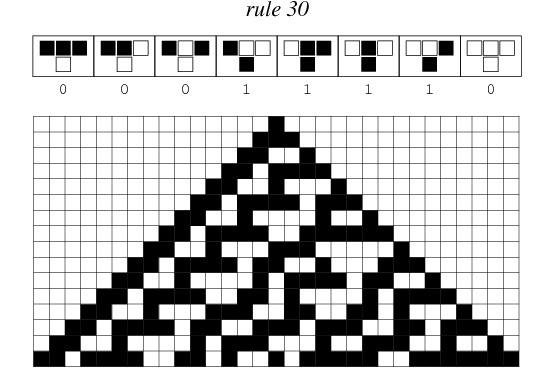 Reglen kaldes Nummer 30, fordi 30 skrives i totalssystemet som 11110. Figuren viser, hvordan en enkelt sort celle udvikler sig.

Her er 250 iterationer af regel 30. Højresiden minder om dekorationen på Cambridge North. På The Aperiodical påstår de, at Cambridge North er regel 135. Det svarer til at tage komplementet til regel 30 – 00011110, så får man 11100001 og spejle det – det bliver så til 10000111, som er binært for 135. I kan lege med endimensionale cellulære automater på Emergent Mind Jeg har lavet nummer 135 til jer:

 

 

 

 

Og nummer 86, som binært er 1010110. Det ligner egentlig også Cambridge North… Men det er der ikke mange andre, der gør.

 

 

 

Om fugle i flok

Lokale regler, som giver overordnede systemer kaldes ofte “emergente egenskaber”. Et eksempel er fugle, som flyver i flok ved at indrette sig efter de umiddelbare naboer. Det bruger man til at computergenerere store flokke af dyr – gnuerne i Løvernes Konge er lavet på den måde – eller menneskemængder. Der er nogen, der mener, det bliver et helt nyt område i matematik at forstå den slags til bunds.

Jeg har skrevet om Cellulære automater på numb3rs-bloggen i 2007. Der kan I finde andre links.