Flyt Verden med Eulers formel.

På Flyt Verden er ikonet for matematik Eulers formel $e^{i\pi}+1=0$ . Hvad laver den der og hvad flytter den mon?

I (PR for) matematikuddannelserne forfiner vi budskabet til Forstå, Forudse og Flyt Fremtiden (Matematik), Forudse Fremtiden (Matematik-økonomi), Tag Del i Teknologiens Udvikling (Mat-Tek).

Alle steder kan man få brug for Eulers formel og den indsigt, den giver.

I gymnasiet møder man eksponentialfunktioner $e^x$ eller med en anden notation: $\exp(x)$ er en funktion. Den kan beskrives og defineres på mange måder, eksempelvis

Den funktion, som løser differentialligningen $f'(x)=f(x)$ og opfylder $f(0)=1$ . (Altså udfra dens vækst – sådan ser I den første gang i gymnasierne.)
Den inverse funktion til den naturlige logaritme $\ln(x)$ . (Sådan gjorde man tidligere i gymnasierne. $\ln(x)$ blev defineret som den stamfunktion til $\frac{1}{x}$ , som går gennem $(1,0)$ .
Den differentiable funktion $f:\mathbb{R}\to \mathbb{R}$ , som opfylder $f(a+b)=f(a)f(b)$ og $f'(0)=1$ .

I 1) bygger man på et (dybt) resultat om, at der finde sådan en løsning. I 2), at en kontinuert funktion har en stamfunktion og en strengt voksende funktion har en invers. I 3) er der igen en forudsætning om, at sådan en funktion findes. Uanset udgangspunkt, så vil $e^x$ opfylde alle tre punkter.

$e^{iy}$ er også en eksponentialfunktion. Jeg skrev om den sidste år og vil ikke gentage det, blot kort: $i$ er en løsning til $x^2+1=0$ – populært sagt en kvadratrod af $-1$ . Det giver en helt ny verden af tal, de komplekse tal, alle $a+ ib$ og man kan lave sig en eksponentialfunktion med komplekse tal som input og komplekse tal som output, $e^{x+iy}= e^x(\cos(y)+i\sin(y))$ . Den opfylder 3) ovenfor og desuden 1 og 2, når man har præciseret dette for komplekse tal. Sætter man $x=0$ og $y=\pi$ får man $e^{0+i\pi}= e^0(\cos(\pi)+i\sin(\pi))=-1$ og vi har Eulers formel. Svingninger er dybt forbundet med komplekse tal via den komplekse eksponentialfunktion.

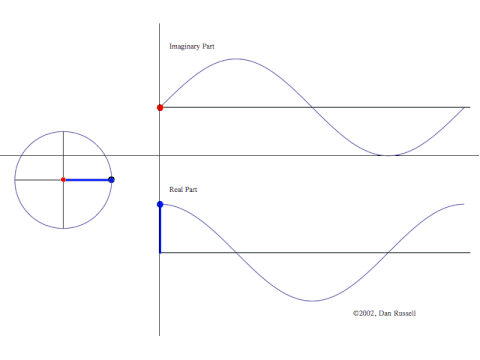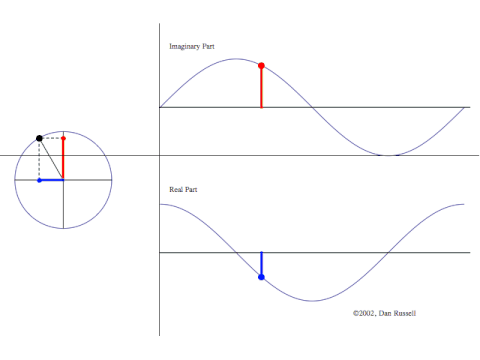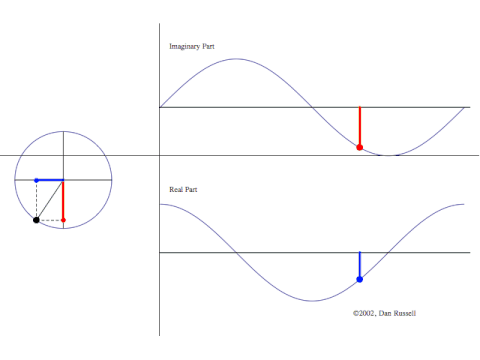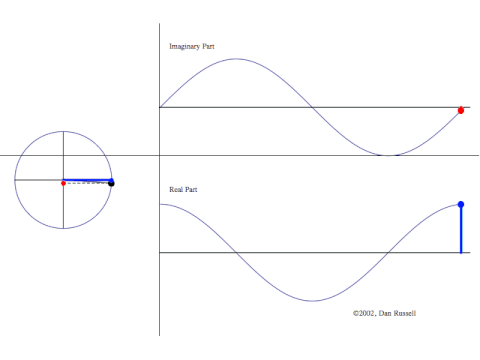complex GIF Man plotter komplekse tal i planen – $x+iy$ er punktet (x,y). Figuren viser punkter på en cirkel, altså $(A\cos(t), A\sin(t))= Ae^{it}$ . Til højre ser man variationen at x-koordinaten (den blå graf) og y-koordinaten (den røde), når man løber rundt på cirklen.

Fra Wikipedia – billedet ovenfor er lagt ned. Nederst plottes $Ae^{it} =A\cos(t)+iA\sin(t)$ som $(A\cos(t), A\sin(t))$ i planen – det bliver punkter på en cirkel. Øverst er kurven $( A\sin(t),t)$

Figuren (fra Wikipedia) viser to situationer som ovenfor (den røde $Ae^{it}$ og den blå $Be^{i(t+k)}$ hvor k er en konstant – faseforskydning) samt summen af de to (den lilla). I nederste billede løber et rødt, et blåt og et lilla punkt rundt på tre forskelige cirkler og danner et parallellogram. Bemærk den samlede effekt på den øverste graf – det er temmelig indviklet. Men med komplekse tal kan man både regne og forstå det bedre.

Og nu forstår og flytter vi verden. Komplekse tal er nyttige, når man:

beskriver vekselstrøm (fase og amplitude)
skal forstå svingninger i økonomi – når man får brug for løsninger til $x^2+1=0$ i sin økonomiske model.
analyserer signaler, billeder,… ved Fast Fourier Transform (uden den, ikke noget digitalt tv)
løser differentialligninger – som kan være model for sygdomsspredning, flow over en flyvinge, EKG,…
beskriver rotationer (og skal bruge kvaternioner)
laver landkort, som skal bevare vinkler

Og der er meget mere. Men kom og læs hos os og bliv klogere. Og flyt så verden – og flyt med. Komplekse tal er kun et lille hjørne af matematikken.