En artikel i Nature Communications om et “nyt matematisk objekt” har givet genlyd. Scutoiden hedder den lille ny. Den kan ses på figur d, hvor to scutoider passer sammen (den grønne og den gule)

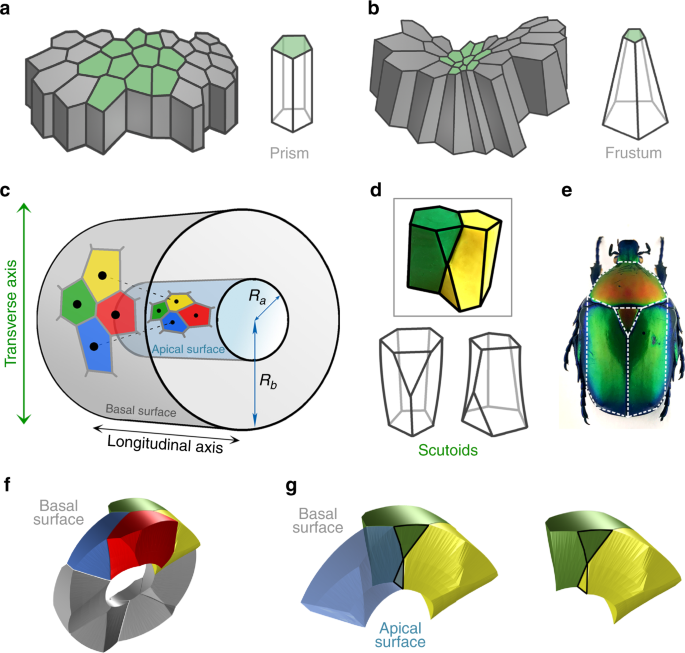
Illustration fra Nature Communications.

Scutoider er (op)fundet af en gruppe forskere – biologer, dataloger, matematikere, som ville forstå, hvordan visse typer væv, epithelvæv, er opbygget. Den slags væv er lagdelt – eller pakket mellem nogle lag. Ifølge artiklen i Nature, er der epithel-celler, som forbinder celler i to (flade) lag. Det har man bl.a. set i bananfluer – drosophila.

Billede fra Wikipedia – cell junctions.

Hvis lagene ikke krummer, er der allerede en fin model, hvor de to lag forbindes med prismer og keglestubbe (a og b på første figur – frustrum er keglestub).

Men hvad nu, hvis lagene krummer? Som eksempelvis når væv er afgrænset omkring en blodåre, tarmene eller noget i den retning?

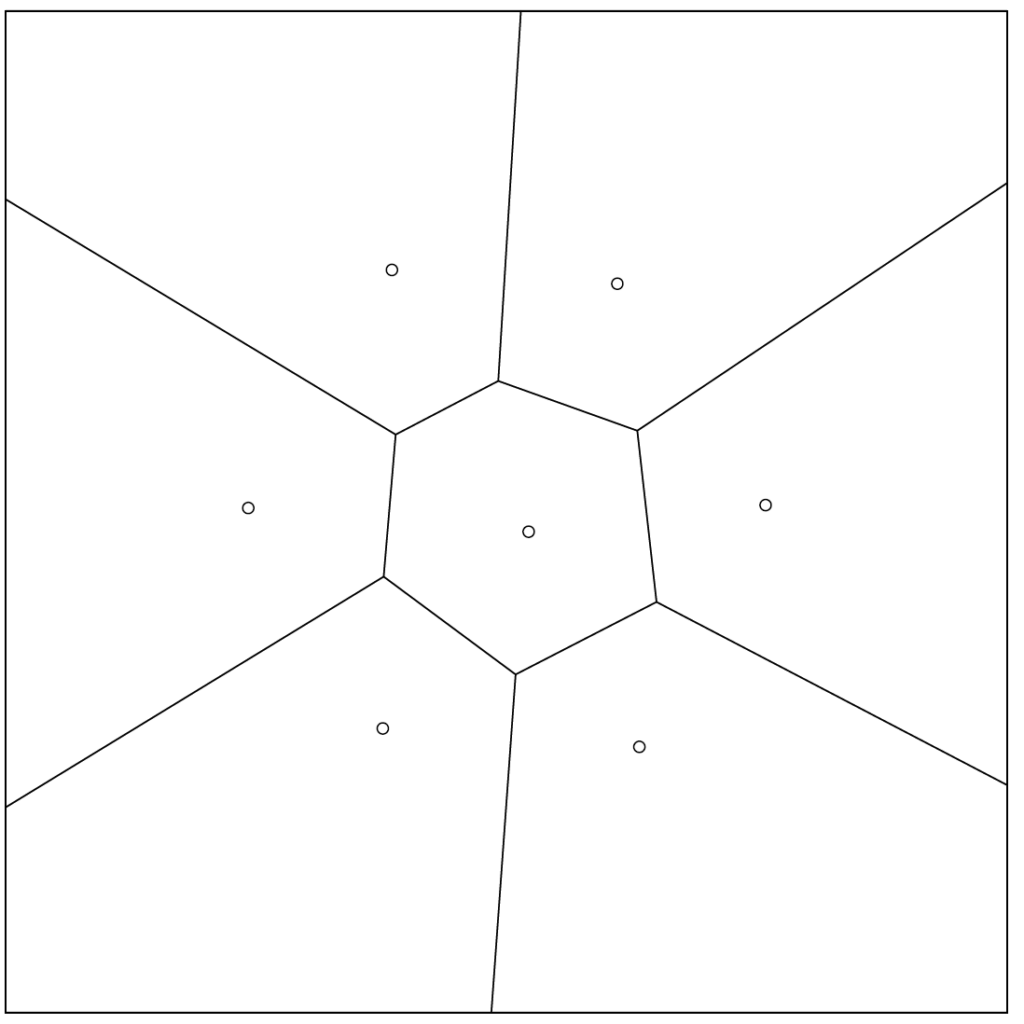
I hvert afgrænsende lag danner cellegrænserne Voronoiceller:

 De røde prikker er centre. Et punkt i en “celle” ligger tættere på det røde punkt i cellen end på noget andet rødt punkt.

Sådan er det altid – uanset, om lagene krummer eller ej. Nu skal to sådanne lag forbindes. I modellen skal der laves en forbindelse fra hver Voronoicelle i det ene lag til hver Voronoicelle i det andet, som man ser i a) og b) i første figur. Når lagene er plane, har man hidtil kunnet gøre det med keglestubbe og prismer – fordi man i det tilfælde har lige mange kanter langs matchende Voronoiceller i de to lag.

Forestiller vi os nu, at de to lag er cylindriske med forskellig radius som i c) og desuden for at gøre det simplere, at cellekernerne ligger “samme sted” bortset fra radiuskoordinaten – mere præcist: Punkter i rummet kan beskrives med en radius, vinkel og en højde. Figuren nedenfor viser radius, vinkel og højde . Cellekernerne på de to forskellige cylindere har altså samme , men forskellig

Hvad sker der så med Voronoicellerne? Bliver de ikke bare “ganget ud” med radius? Nej! For afstande mellem punkter på cylinderne bliver ikke bare ganget:

Afstande på en cylinder kan findes ved at “rulle cylinderen ud” til et rektangel og måle i planen.

Er cylinderen h høj og har radius r, er rektanglet h på den ene led og på den anden. Med samme højde og radius R er det h på den ene led og på den anden. Og så ændrer Voronoicellerne sig kvalitativt. På billederne nedenfor, som Jakob Gulddahl Rasmussen har lavet til mig, er 6-kanten omkring det midterste punkt blevet til en 4-kant, når der strækkes på den ene led. Linjestykkerne er midtnormaler mellem par af punkter (på linjestykket er der lige langt til to af “cellekernerne”) og de slutter, når de møder andre midtnormaler. I kan lege med, hvordan det ændrer sig, når man strækker på den ene led, eller  når man flytter  i en af de mange apps, der findes. Her er en på University of Michigan. – Se mere på Numb3rsbloggen

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Og så kommer problemet: Man skal indsætte en forbindelse mellem celler med forskelligt antal kanter. Det kan ikke være en keglestub eller et prisme, for de har samme antal kanter i øverste og nederste flade. Det er her Scutoiden skal bruges. I figuren øverst ser man scutoider mellem femkanter og sekskanter. Den ene kant i scutoiden deler sig et stykke nede i to kanter. (Hvis man flytter delepunktet helt ned (eller op), får man et prisme, men det er ikke sådan, vævet opfører sig.)

Scutoidens sider er ikke plane – de krummer. Men det har vist sig, at det er sådan, det ser ud, når man kigger nærmere på en bananflue, eller hvad man nu har.

Scutoider bruges nu til at lave modeller for epithelvæv. Man gætter på, at de kan bruges til at lave kunstigt væv.

Man kan købe 3d-printede scutoider, der er artikler om scutoider her, der og allevegne. Jo, den lille ny er berømt.

Selvfølge har den uforlignelige Matt Parker lavet en video om scutoider. Med piberensere… Og interview med matematikeren bag.

Om det er ny matematik, kan man bestemt godt diskutere. Men det er ny indsigt og giver nye anvendelsesmuligheder i et samarbejde mellem mange fagområder. Det er da helt fremragende!