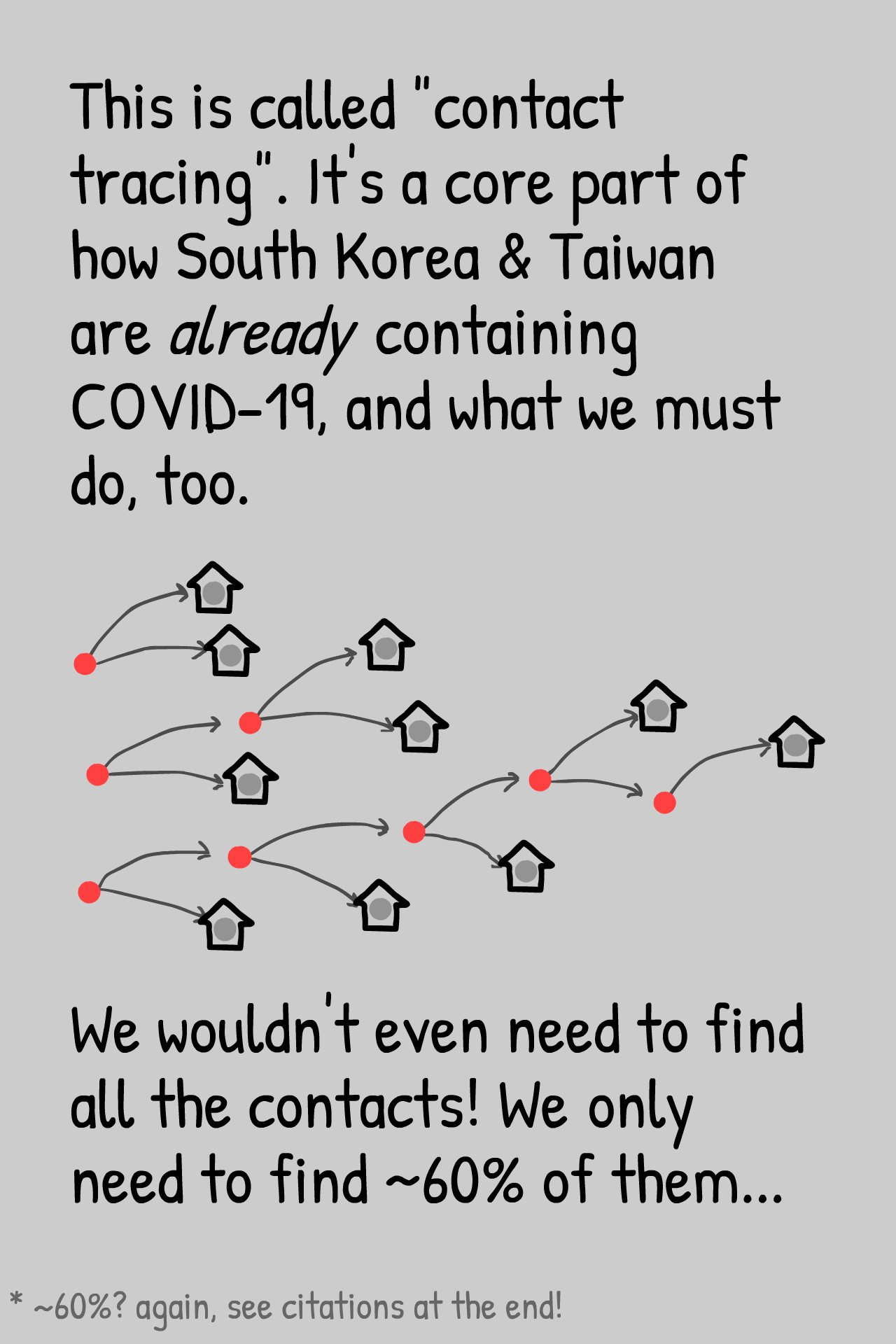
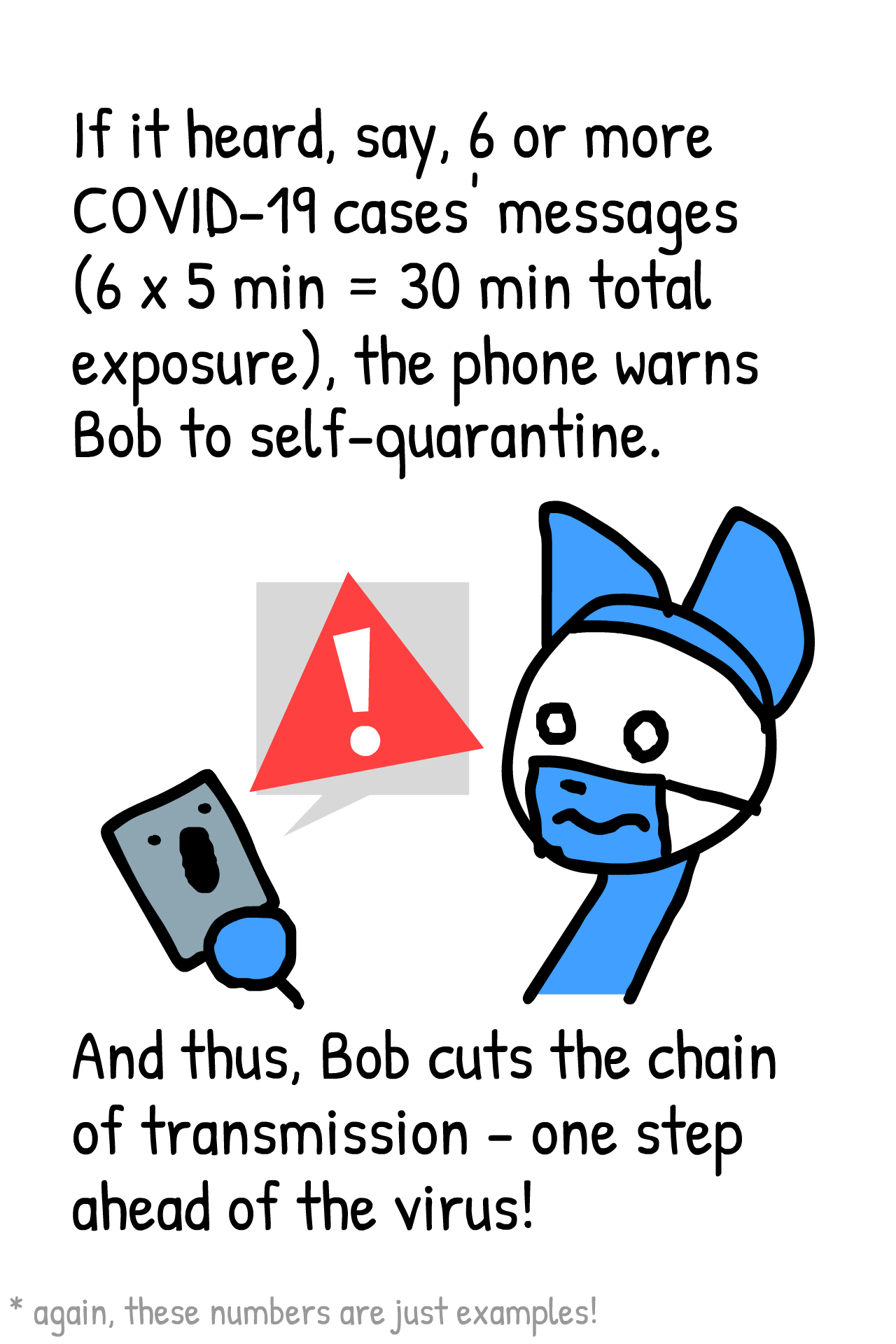
Tegneserien nedenfor er lavet af Nicky Case, som også står for grafik og kodnng på den fantastiske side What happens Next? – gå først til den, hvis ikke, du har været der før. Det er sublim formidling.

Hvordan kan en kontaktopsporingsapp holde på dine hemmeligheder.

Tegneserien beskriver en konkret idé til en smitteopsporingsapp, men principperne bruges af flere og er i øvrigt ret velkendte fra feltet med kryptering, deling af hemmeligheder, at regne på/med information, man ikke kan se… hvor både matematik og datalogi er helt nødvendige. Det ser ud til, at man her bruger en lidt anden teknik  end den, vi tit hører om med primtal og andet i den talteoretiske/algebraiske boldgade.
På AAU er der også arbejde med smitteopsporing. Her er et spritnyt preprint – lavet i samarbejde mellem Institut for Matematik og Insitut for Elektroniske Systemer.

Hvor er matematikken i tegneserien (og appen): Jo, der er noget med pseudotilfældige tal. (“uniquely random gibberish”, som der står i tegneserien)  Det har jeg skrevet om før – eksempelvis her.

Alice får en engangsadgangskode (OneTimePasscode, OTP, hvis I vil Google). Bag dem ligger også pseudotilfældighed: Der skal ikke være let gennemskueligt system i, hvordan den næste kode bliver, når man har set en stribe af dem. Så ville man måske selv kunne lave sig en ved at hacke sig ind på dem, der sendes til Alice og andre.

Der bruges også et “cukoo-filter”, som er opkaldt efter gøgeunger, der vipper andre fugleunger ud. Det skal sikre, at det kun er relevant information (gøgeunger), der sendes til eksempelvis Bob i tegneserien.

Test af pseudotilfældige tal

Man skal til appen bruge en frembringer af tilfældige tal, en PRNG (PseudoRandomNumberGenerator). Den er “Pseudo” og der er altså et underliggende system i, hvordan tallene laves. Der er mange tests for, om det så er “tilfældigt nok”. Overordnet skal talene opføre sig som noget tilfældigt ville gøre. Det amerikanske NIST (National Institute for Standards and Technology) har beskrevet det og giver mange eksempler på den slags tests. Det er en statistisk test med 0-hypotesen: “Denne følge af tal er tilfældigt frembragt”. Så kan man skrue op og ned for, hvad der skal til for ikke at dumpe den test – justere den krævede p-værdi, om man vil.

Givet 20.000 tal, som enten er 0 eller 1. Læg dem sammen (ikke binært –  101 giver 2). Med 20.000 skal man få et tal mellem 9654 og  10346. Det vil rigtige tilfældige tal bestå med sandsynlighed 1-10^(-6). (Der er ca. lige mange 0 og 1 i følgen)

NIST gør følgende, som egentlig er samme ide:

For en følge  af 0’er og 1’er

lægger man sammen som følger. For hvert 1 lægges 1 til, men for hvert 0 trækkes 1 fra. Smart skrevet. Man summerer .
Eksempel: 11001010010111 giver S_obs=1+1-1-1+1-1+1-1-1+1-1+1+1+1=2.

Udregn hvor er antal bit (her 12).

Dette vil være normalfordelt med middelværdi 0 og spredning 1 for en sand tilfældig følge, så man kan undersøge, om hypotesen skal forkastes ved at udregne arealet af det, der ligger længere væk fra 0 i normalfordelingen. Det giver p-værdien. Man bruger mere end én test – se mere hos NIST eller det tyske BSI, Bundesamt für Sicherheit in der Informationstechnologie.

 

Vil man have rigtigt (sande) tilfældige tal, kan de hentes hos kvantefysikerne – henfald og bip i en Geigertæller er sandt tilfældige. Man kan hente det fra atmosfærisk støj på random.org og sikkert andre steder. Men det er dyrt, langsommeligt og dermed ikke smart til eksempelvis en smitteopsporingsapp.

En PRNG er en algoritme, som tager et input (et “seed”) og fra det producerer en streng af bits, som opfylder kriterierne ovenfor. Samme “seed” giver samme bitstreng. Men strengen skal se helt tilfældig ud – bestå de tests, NIST og andre har. Det er altså en ganske snedig algoritme.

Et eksempel på sådan en er Mersenne Twister, som bruger Mersenne primtal. Den er hurtig, men knap så sikker – man kan gætte systemet og derefter gætte næste bit. Langsommere, men mere sikker, er Blum Blum Shub, som gør som følger:

Man finder to primtal, p og q, som er meget store. Så ganger man dem og får M=pq. Nu vælges en startværdi – et “seed” x0 og udregner x2, x3,…. Talfølgen er givet ved at tage det seneste tal i rækken, xn, kvadrere det og udregne resten ved division med M.

Eksempel: p=7, q=11, så er M=77. Lad x0=15, så er x0^2= 225. Divider med 77. Resten er 225-154= 71.
Næste tal 5041-5005=36, 1296-1232=74, 5476-5467=9, 81-77=4, 16, 256-231=25

15, 71, 36,74,9,4,16,25

det ser da ret tilfældigt ud. Man bruger ikke direkte tallene fra output, men genererer en bit fra hvert af disse tal – f.eks. et 1 tal, hvis der er et ulige antal 1’er i xn skrevet binært…

Sikkerheden i Blum Blum Shub bygger bl.a. på, at det er  svært at finde p og q, selvom man måske kan finde M.

Er det så helt fuldstændig sikkert at bruge sådan en app? Se det kommer an på implementeringen. Man kan jo gøre noget andet, end man påstår. Så det er godt, man i dette tilfælde har adgang til koden bag appen. Så kan dem, der forstår det, kigge efter. Andre kan finde en, der forstår det og som man stoler på.