På grænsen mellem matematik og biologi sker der rigtig meget lige nu. Biologiske problemstillinger er komplekse, der er bunker af data og der er ikke mindst store og væsentlige problemer. For nylig har Reidun Twarock etableret en forbindelse mellem geometri og symmetri og hvordan virus udvikler sig. Og det har givet helt ny indsigt i både virus og i øvrigt også design af malariavaccine. Jeg hørte første gang Reidun Twarock holde foredrag om det område i 2009 i Novi Sad og igen i Oxford i april i år, så nu er jeg inspireret. Billedet viser vira (virusser, hvis man ikke er sprogrevser). De forskellige farver er forskellige proteiner. Tak til Reidun for at have forklaret mig nærmere om hele dette felt, at have svaret på mine spørgsmål og sidst men ikke mindst for at lave så cool matematik. Læs eventuelt mere i nogle slides, hun har brugt. Eller find et foredrag med hende på YouTube eksempelvis her eller her.
Røntgenstruktur af vira (fra Reidun Twarock)
Virus er pakket ind i et ikosaeder. DNA (og RNA) er for de mange virustyper pakket ind i en capsid, en skal af proteiner, som for de fleste vira er et ikosaeder. Altså en bøtte lavet af proteiner, som DNA sidder indeni. Det har vi vidst siden Crick og Watson (1956) – det er en del af det “genetisk økonomiske princip”. (Genetic economy, hvis I vil Google).
Ikosaederet har 20 sideflader, som allesammen er ligesidede trekanter.
Ikosaederet har “mest” symmetri blandt de platoniske legemer – polyedere, hvor alle sideflader er ens. Kender man en side af et ikosaeder, giver det de 19 andre. Og der er rotations symmetri, som bringer ikosaederet over i sig selv. Rotationssymmetrierne for ikosaederet udgør en gruppe af orden 60. Den største rotationsgruppe i 3D. (Den største endelige undergruppe af matrixgruppen SO(3), for dem, der ved, hvad det betyder. Nærmere bestemt er det A5, den alternerende gruppe.) Der er kun en større gruppe symmetrier, nemlig 
Symmetri på overfladen Donald Caspar og Aaron Klug (Nobelpris 1982) opdagede i 1963, at områder på overfladen har endnu mere symmetri – på hver af de trekantede sider af ikosaederet er der yderligere symmetri i placeringen af de forskellige proteiner, der sidder på overfladen. Den nye indsigt er, at symmetrien fortsætter ind i ikosaederet og giver information om, hvordan dna og rna pakker sammen og hvordan virus udvikler sig. Den forståelse giver nye angrebsmuligheder for medicin.
Man har altså på hver af siderne af ikosaederet et “mønster”, som kan findes ved at tage mønsteret på en af trekanterne og rotere det rundt til de andre. Hvilke muligheder er der så?
En mulighed er, at hver side er opdelt i mindre trekanter, hvor proteinerne sidder i hvert hjørne. Så passer puslespillet sammen i kanterne. Disse muligheder kortlagde Caspar og Klug ved at se på, hvordan man kan folde et ikosaeder ud og anbringe det på et bikube (heksagonalt) mønster.
Men man ved, nogle vira har femkanter med protein 1 i hjørnerne og protein 2 midt i. Og man kan ikke lave et “bikubeagtigt” mønster med femkanter. De passer simpelthen ikke sammen.
Symmetri med orden 5. Tværsnit ind igennem virus, som viser, hvordan strukturen udvides ind gennem det indre af ikosaederet. (Billede fra Reidun Twarock)
De nye bidrag er
- En fliselægningsteori for vira med flere typer fliser – end trekanterne hos Caspar og Klug. Herunder de femkantede strukturer, som eksempelvis optræder i HPV-virus og andre Polyomavira. (Fodboldspillende læsere ved jo allerede, at man kan bruge femkanter til at dække med, hvis blot man har andre byggeblokke også. – Det har man jo på en traditionel fodbold.)
- Udvidelse af symmetrierne indad i ikosaederet – affin udvidelse hedder det. Det bruger symmetrigrupper og gitterstruktur, altså krystalgrupper i det 6-dimensionale rum, som vi så det tidligere på bloggen i forbindelse med kvasikrystallerne.
- Ved at bruge 3D-fliselægning (og ikke bare 2D på overfladen af ikosaederet) har Twarock et.al. udviklet nye modeller for virusarkitektur, som giver flere muligheder end bare at udvide indad fra 2D-fliserne.
Strukturen af HPV-virus
HPV har lokale grupper med fem proteiner – de kaldes pentamerer. Det har 72 pentamerer. 12 af dem sidder, så de passer med den symmetri, der allerede er i ikosaedergruppen (omkring akser, der roteres rundt og tilbage i sig selv med fem “moves”.) Men de resterende 60 er lokale symmetrier, altså ikke det, der allerede er i ikosaederet. De roteres så over i hinanden. (Forestil jer femkantede blomster i tapetmønstrene fra sidste blogindlæg. De flyttes over i hinanden, men har selv noget yderligere symmetri.)
Viral fliselægningsteori kan forklare denne struktur. Det er aperiodisk a la Penrosefliselægning.
Viral fliselægning. Flere typer fliser.
Hvordan samler virus sig – assembly modeller.
Nu ved man altså, at der er sammenhæng mellem systemerne på overfladen og byggeblokkene inde i virus. Næste spørgsmål er, hvordan opstår systemet – hvordan bygges sådan en capsid med indeholdende virus? (Hvis man har leget med FoldIt, som er et spil, hvor man folder proteiner, så kender man problemet. Hvordan folder proteiner sammen mest effektivt.) Hvordan finder virus den/de mest effektive måde/måder blandt de oceaner af muligheder, der er for at samle byggeblokkene. Det har gruppen bag ovenstående også løst. Det gælder om at samle byggeblokkene udfra proteiner. Hver proteinbyggeblok binder først til genomet og derefter til de andre byggeblokke via protein/protein interaktion. Det viser sig, at de mest effektive samlevejledninger og derfor dem, naturen bruger, svarer til at hver kontakt mellem genomet og capsidskallen sker præcis en gang i hver position, altså hvert hjørne. Så byggemulighederne er en tur rundt på overfladen, hvor man besøger hvert hjørne præcis en gang – grafteoretikerne kalder det en Hamiltonsk sti.
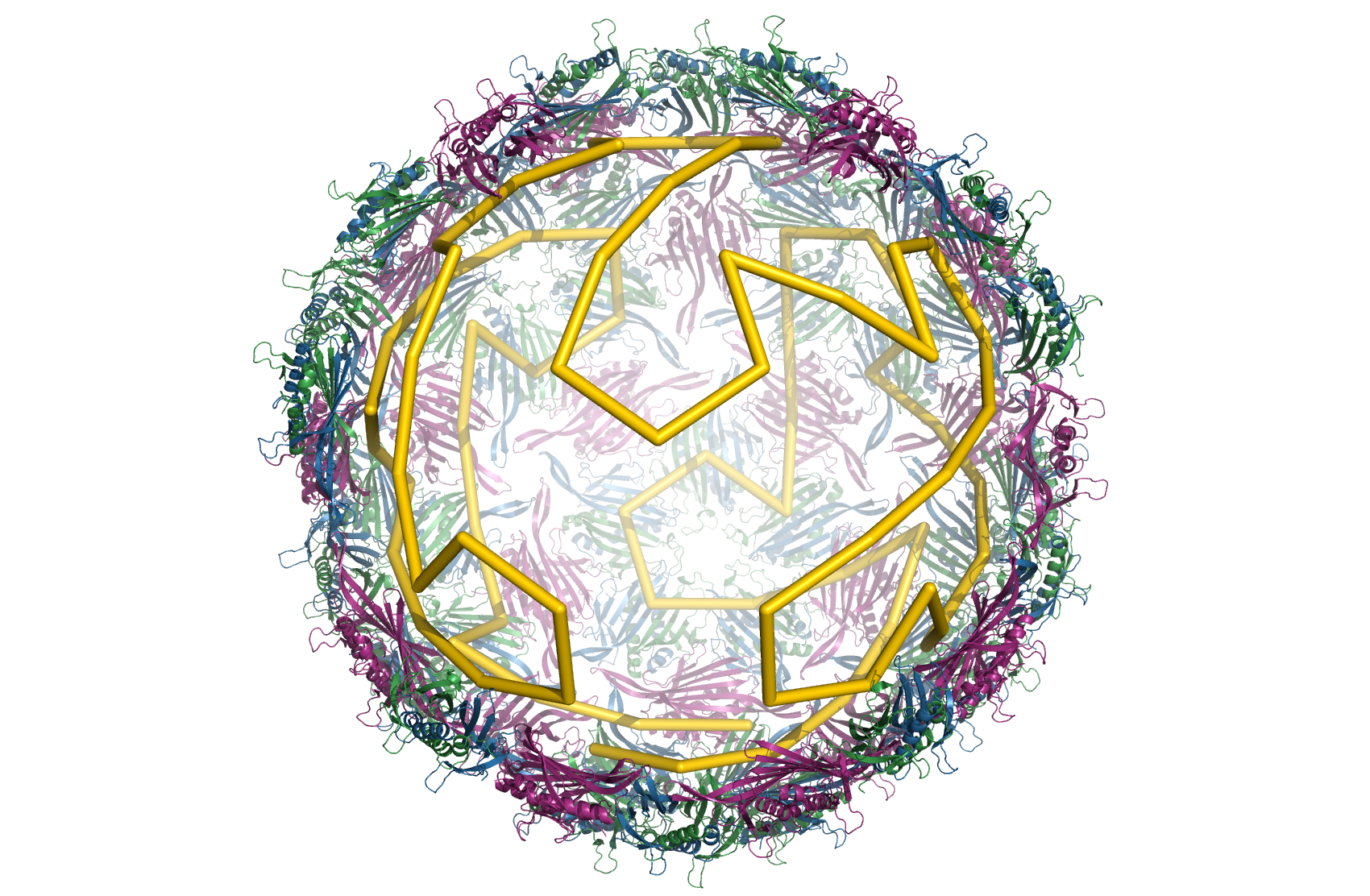
Den gule sti er en Hamiltosnsk sti mellem hjørnerne af byggeblokkene. Bemærk, at man ikke behøver gå på alle kanterne. (Billede fra Reidun Twarock)
De nye indsigter har givet et paradigmeskift i hvordan man forstår “assembly” for virus og dermed mulighederne for at bekæmpe sygdom. Det er en virkelig flot eksempel på, hvordan matematik bidrager til ny forståelse og nye opdagelser i biologi.