George Boole blev født 2.november 1815. Han var matematiker, filosof og er idag nok især kendt som logiker. 200-året for hans fødselsdag fejres hele året . Der er Boole2school undervisningsmateriale, konferencer og meget andet. I 1849 skrev Boole “An Investigation of the Laws of Thought, on which are founded the mathematical theorries of logic and probabilities.” Der står meget, men det væsentlige er det, der idag kalde Boolesk algebra – reglerne for at “regne” med matematiske udsagns sandhedsværdier. Et matematiske udsagn kan være sandt eller falsk. Her er noget konkret at tænke på:
George Boole blev født 2.november 1815. Han var matematiker, filosof og er idag nok især kendt som logiker. 200-året for hans fødselsdag fejres hele året . Der er Boole2school undervisningsmateriale, konferencer og meget andet. I 1849 skrev Boole “An Investigation of the Laws of Thought, on which are founded the mathematical theorries of logic and probabilities.” Der står meget, men det væsentlige er det, der idag kalde Boolesk algebra – reglerne for at “regne” med matematiske udsagns sandhedsværdier. Et matematiske udsagn kan være sandt eller falsk. Her er noget konkret at tænke på:
Udsagn P: Kurt er mindst lige så høj som Frede.
Udsagn Q: Nilen er længere end Gudenåen.
Vi ved, at Q er sandt. Hvis vi nu ikke ved, om P er sandt, så kan vi heller ikke vide, om udsagnet “P er sandt OG Q er sandt” er sandt. Det er det, hvis P er sandt. Og ellers er det falsk. Men udsagnet “P er sandt ELLER Q er sandt”, er sandt, uanset hvad P er, eftersom Q jo er sandt. Den slags ræsonnementer satte Boole i system, så vi nu kan få en computer til at lave følgeslutninger som ovenfor og så vi kan lave mere avancerede ræsonnementer uden at få hovedpine – Er udsagnet “(P er ikke sand OG Q er sand) ELLER P er sand” sandt? Man skal også kunne “negere” et udsagn. Udsagnet nonP er sandt hvis og kun hvis P er falsk, og det er falsk hvis og kun hvis P er sandt.
Sandt og falsk noteres ofte som hhv. 1 og 0. OG som multiplikation, ELLER som +.
Lad os nu gå ud fra, P er falsk, så P har sandheds værdi 0 og Q har værdi 1. Sandhedsværdien af P OG Q er så 0 gange 1 =0.
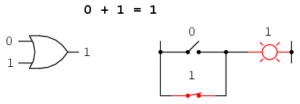
Sandhedsværdien af P ELLER Q er 0+1=1
Det giver følgende tabel over regning med sandhedsværdier: Lad mig skrive “x” for multiplikation – husk, det svarer til sandheds værdien af udsagnet P OG Q, når vi kender sandhedsværdien af P hhv Q: 0x0=0, 0x1=0, 1×0=0, 1×1=1 Det ser jo fint ud. Nu til +, som svarer til P ELLER Q: 0+0=0. 0+1=1. 1+0=1, 1+1=1 Hovsa! Jo, hvis både P og Q er sande, så er udsagnet P ELLER Q naturligvis sandt. Altså 1+1=1.
Nu kommer det smarte. Man kan sammensætte regningerne, så udsagnet (P OG Q) ELLER (R OG S) har sandhedsværdi (PxQ)+(RxS), hvor jeg har ladet P,Q,R,S stå for sandhedsværdien af hhv. P,Q,R,S.
Har man OG, ELLER og NON, kan man lave “medfører”: P MEDFØRER Q betyder, at hvis P er sand, så er Q sand. Det er sandt, hvis P er falsk (uanset hvad Q er) og hvis Q er sand (uanset hvad P er) – det kan man tænke over eller lade være en definition…. P medfører Q har har samme sandhedsværdi som (non P) ELLER Q, så vi kan altså bygge det fra, hvad vi allerede har. Her er en sandhedstabel for nogle udtryk. JEg har skrevet S og F i stedet for 1 og 0 – jeg tror, det er lettere at overskue for læsere, der ikke er vant til notationen med 0 og 1.
| P | Q | P OG Q | P ELLER Q | NON P | P MEDFØRER Q |
| S | S | S | S | F | S |
| S | F | F | S | F | F |
| F | S | F | S | S | S |
| F | F | F | F | S | S |
Her kan man lave sine egne sandhedstabeller.
Claude Shannon indså, at Boolesk algebra kunne bruges til at regne på Elektroniske kredsløb: Elektronikversionen af ELLER – en parallelforbindelse. Hvis der kommer 0 ind af den ene og 1 af den anden, så kommer der 1 ud – lampen lyser, hvis der er forbindelse den ene vej.
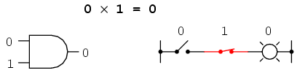 Her er en OG gate – en serieforbindelse. Begge skal være sande, før lampen lyser.
Her er en OG gate – en serieforbindelse. Begge skal være sande, før lampen lyser.
Et andet eksempel på Boolesk algebra er regning med mængder. I stedet for udsagn har vi delmængder af en mængde M. Vi tænker på sandheds værdien af “x tilhører B”, hvor B er en delmængde af M og x er et element i M. Det er ikke så svært at se, at OG bliver fællesmængde, ELLER foreningsmængde og NON komplementærmængde.