går til Andrew Wiles. For beviset for Taniyama Weil formodningen og dermed Fermats sidste sætning.

Tilføjet klokken 15: Jeg skriver ikke om Fermats Sidste Sætning. Det har jeg jo gjort i indlægget Kan man skrive en børnebog om Fermats Sidste Sætning.

Hvsi I vil læse mere, er der materiale på Abelprisens hjemmeside. På engelsk og naturligvis på norsk. (oversættelsen af Axel Bellos’ populære fremstilling til norsk er ikke imponerende, men de får muligvis rettet den til. Især hvis jeg får brokket mig… Men den engelske er fin.)  Se også Arne Slettsjøs forklaring på, hvordan Fermat viste sin store sætning for n=4 ved at bruge et resultat, som Diofantus  havde bevist.

Nå, blogge eller ikke blogge om -dag? Det er jo hamrende uinteressant, at datoen idag har noget at gøre med de første decimaler af . Hvis du har undgået at løbe ind i begrundelsen for at holde -dag, så er den her: I USA skriver man datoer med måneden først, så 14.marts bliver 3/14. Og de første cifre i decimaludviklingen af er 3,14.

Pi Pie fra Delft.

Jeps, det er en søgt undskyldning for at spise pie og tale om , men lad os nu hoppe på den. Og ellers så fejrer vi bare Einstein.

er forholdet mellem omkreds og diameter i en cirkel. Ikke bare en enkelt cirkel, men alle cirkler har det samme forhold.

er irrationelt og ovenikøbet transcendent:

• De rationale tal er de tal, der kan skrives som en brøk p/q mellem hele tal. De irrationale tal er de reelle tal, der ikke kan skrive som en sådan brøk. At er irrationalt ved mange fra gymnasiet og matematikerne har vidst det i mere end 2000 år. I 1761 viste J.H. Lambert, at er irrationalt.
• Tal, der er rødder i polynomier med heltalskoefficienter kaldes algebraiske. Eksempelvis er  rod i andengradspolynomiet og det komplekse tal er rod i . Alle tal er sådan set rødder i polynomier: er rod i polynomiet , så det vigtige er koefficienterne.  Et polynomium , har heltalskoefficienter, hvis alle koefficienterne er hele tal. Tal, der ikke er rødder i et polynomium med heltalskoefficienter kaldes transcendente. At er transcendent viste von Lindemann i 1882.

Det er forbavsende hvor mange steder, dukker op. Tidligere på bloggen i Mod det uendelige univers havde vi Eulers resultat om, at . Så der kommer nok lidt overraskende ind.

Periodiske fænomener får ofte bragt ind i billedet via sinus og cosinus. Men der er også i statistik.

Tæthedsfunktioner for normalfordelingen med forskellig middelværdi oo spredning.

Normalfordelingens tæthedsfunktion indeholder nemlig : Tæthedsfunktionen for normalfordelingen med middelværdi og spredning har udtrykket  . Man kan finde sandsynligheden for, at en stokastisk variabel, som er normalfordelt med disse parametre, ligger i intervallet mellem a og b, ved at udregne . Det må I få mere om i et andet blogindlæg eller læse her, hvor Ege Rubak forklarer, hvorfor normalfordelingen er så vigtig.

Det er ikke en tvangstanke hos matematikere, at der skal puttes i alting. Det kommer ud af krav til modeller, af svingninger og sommetider virkelig overraskende, hvor man skal gruble over, hvad grunden er.

Der er kvaternioner i computerspil, i flysimulatorer og i styring af robotter, der skal rotere. Hvad mon de laver der?

Kvaternionerne blev opdaget af den irske matematiker og fysiker, W.R. Hamilton. Han fik den fundamentale indsigt om dem, da han spadserede langs Royal Canal i Dublin og der sidder nu en

Mindepladen på Broome Bridge.

mindeplade på den bro, Broome Bridge hvor han efter sigende skriblede ligningerne

, , ,  .

Kvaternioner er tal, på formen a+bi+cj+dk, hvor a, b, c, d er reelle tal og i,j,k er symboler, som  kan lægges sammen som vektorer med 4 koordinaterog ganges sammen efter reglerne ovenfor. altså samme system som med de komplekse tal, men der er nu kommet j og k med. Eksempel:

og hvor jeg brugte reglerne ovenfor, da jeg gangede i,j og k med hinanden. Bemærk, at og tilsvarende for de andre produkter, der ikke er nævnt ovenfor.  i,j og k antikommuterer.

Kvaternionerne er en divisionsalgebra eller et skævlegeme. I får ikke regnereglerne for divisionsalgebraernes addition og multiplikation, men jeg har brugt mange af dem ovenfor. De reelle tal og de komplekse tal er også divisionsalgebraer (med kommutativ multiplikation). Tager man udgangspunkt i addition af vektorer og forsøger at finde en multiplikation, der “matcher”, kan man kun gøre det for for har man en multiplikation, der giver  Cayleytallene, men der er multiplikation ikke associativ: (ab)c er ikke nødvendigvis a(bc).

Hvad har det med computerspil og jagerfly at gøre?

En rotation i det 3-dimensionale rum kan beskrives ved en rotationsakse og en vinkel. Har man valgt sig et koordinatsystem, kan alle rotationer beskrives som en kombination af rotation om x-aksen, derefter om y-aksen og derefter om z-aksen. Man kan altså beskrive det ved de tre vinkler.

Roll, Pitch og Yaw

For jagerpiloter hedder det “roll”, pitch” og “yaw”, når man roterer om flyets egne interne akser. Man kan lege med Roll Pitch og yaw her (klik på Euler angles i øverste højre hjørne). Det er naturligvis ikke det samme som at vælge nogle faste akser, som ikke følger med flyet, men der er omregninger frem og tilbage mellem diverse systemer af vinkler og akser. Man er i øvrigt (heller) ikke enige om, hvilken akse, der roteres om først, så man skal være vågen, hvis man henter formler flere steder fra. Orienteringen  af et objekt i  rummet kan altså beskrives med tre vinkler, som siger, hvordan objektet er roteret i forhold til nogle faste x,y,z akser.De kaldes også Eulervinkler. Samme position kan svare til flere forskellige vinkler – hvis vi måler i radianer, gentager de sig for hver ;  i grader er perioden 360. Bemærk, at det drejer sig om orienteringen af et 3-dimensional objekt, ikke bare den retning, eksempelvis næsen på flyet peger i.

Så den rotation, der er lavet for at bringe flyet i en bestemt position, kan beskrives med tre vinkler, altså et punkt (u,v,w) i . Og man skal ikke bruge mere end de vinkler, der er i kassen, som er afgrænset af

, ,

for at være sikker på, man har alle rotationer med. Kunne man mon nøjes med færre vinkler – giver nogle vinkler de samme rotationer? (Svar: Ja) Hvordan er kassen “limet sammen”? Hvordan svarer punkter i den ene ende til dem i den anden, top til bund og front til bagside? Hvordan ser det ud, når et fly ændrer sin position og går via “ydervinklerne”. M.a.o. hvordan ser det ud i vinkler, når et fly laver loop, barrel roll og andre luftakrobatiske manøvrer? Hvordan laver man en kontinuert rotation, der bringer flyet til en bestemt position i rummet, altså en kontinuert kurve i mængden af rotationer. Det er der, det bliver interessant. Og hvor beskrivelsen med Eulervinkler må give op.

Matrixbeskrivelse.

En rotation kan beskrivesmed en 3×3 matrix, hvis første søjle er koordinaterne for vektoren [1,0,0] efter rotation, anden søjle er koordinaterne for [0,1,0] efter rotation og tredje søjle er koordinaterne for [0,0,1] efter rotation. Som udgangspunkt er der 9 tal i en 3×3 matrix, men en rotations matrix skal opfylde en stribe ligninger, som kommer udfra at søjlerne har længde 1, står vinkelret på hinanden og udgør et højrehåndssystem. (Da de jo er resultatet af at rotere basisvektorerne). Rotationsmatricerne udgør delmængden SO(3) af 3×3 matricerne. Det er en 3-dimensional delmængde af det 9-dimensionale rum, som svarer til de 9 tal i en 3×3-matrix. Enhver rotationsmatrix kan skrives som et

Rotationsmatricer for rotation om x,y,z aksen. Billede fra Wikipedia.

produkt af matricer, der svarer til rotation om x,y,z akserne. Altså udfra tre vinkler.

Produktet AzAyAx

Med vinklen bliver den samlede rotation

Jeg har brugt additionsformler for sinus og cosinus. Bemærk, at rotationen ikke afhænger af og hver for sig, men kun af deres sum. Altså at eksempelvis giver samme rotationsmatrix uanset hvad er hver for sig. Det betyder, at beskrivelsen med vinkler er fejlagtig. Det ser ud somom, der kun er to “retninger” at vælge imellem, når man skal rotere væk fra positioner med , men der skal være 3.

Dimensionen af mængden af rotationer er 3. Det er et ægte praktisk problem, som får robotter til at gøre pludselige skift på 180 grader eller (mindre alvorligt) computerspil til at se mystiske ud, når jagerfly kommer i position med eksempelvis næsen opad. (Den ubestemthed, der er i situationen, hvor man ikke kan se, hvad de to vinkler er, kan have sære effekter.) Så der er en god grund til at gøre noget ved det.

Man kan tænke på en lidt analog situation, hvor man nærmer sig Nordpolen langs en meridian, altså med fast længdegrad. man har altså breddegrad, der vokser mod . Kigger man i systemet af længdegrader og breddegrader, vil man ikke kunne se, at en kurve op til Nordpolen langs Greenwichmeridianen (længdegrad =0) og væk fra Nordpolen langs en meridian med vinkel , slår et knæk på Nordpolen. Eller at kurven, der går op langs Greenwichmeridianen og væk langs datolinjen faktisk ikke knækker. Det skyldes, at systemet med længde- og breddegrader klemmes sammen i Nordpolen, så breddevinkel og længdegrad hvadsomhelst, er samme punkt, nemlig Nordpolen.

Kvaternionerne er bedre: 

Kvaternioner med længde 1 beskriver rotationer. Til en sådan kvaternion q=w+xi+yj+zk svarer rotationsmatricen

Som man kan se, giver kvaternionen -q samme rotation, men det er den eneste “sammenlimning”, der sker, når man afbilder fra enhedskvaternionerne til rotationerne. Enhedskvaternionerne udgør en 3-dimensional kugleflade – det er jo vektorer med 4 koordinater af længde 1. Effekten af at bruge kvaternioner til at beskrive rotationer er, at man har den rigtige dimension og i analogi med eksemplet med Nordpolen, nu kan se forskel på, om kurver af rotationer knækker eller ej, men der er andre gevinster: Skal man beskrive en kurve af rotationer, altså rotere fra en position til en anden gennem mellempositioner, så er det meget let at gøre med kvaternioner – man laver en kurve r(t) i , som starter i q1 og ender i q2 og ikke passerer 0. Nu skal man sikre sig, den holder sig indenfor kvaternioner med længde 1, men det er let. Man bruger bare r(t)/|r(t)|, altså dividerer med længden hele vejen. Skulle man gøre det med rotationsmatricer, var det ikke så let – en matrix, der ikke er en rotationsmatrix kan ikke med et snuptag korrigeres ind til rotationsmatricerne.

I tirsdags annoncerede ACM, at Turingprisen for 2015 går til Whitfield Diffie og Martin E. Hellman. De får prisen for noget, vi idag betragter som ganske selvfølgeligt, nemlig “public key kryptering”, kryptering med offentlig nøgle. Kryptering har været kendt i mange former igennem historien, læs for eksempel Simon Singhs Kodebogen.

Merkle, Hellman og Diffie i 1975.

Men indtil Diffie og Hellman skrev artiklen New directions in Cryptography i 1976, kunne man kun sende hemmelige beskeder til hinanden, hvis man først var blevet enige om en nøgle, altså, hvordan man ville kryptere og dekryptere. Og nøglen skulle være hemmelig. Så man skulle altså først have en form for hemmelig kommunikation, før man kunne udveksle mere hemmelig information. (Ralph Merkle tabte kapløbet om at komme først, men han havde mange af de samme ideer. Desuden har man senere fundet ud af, at det britiske GCHQ havde tilsvarende ideer, men holdt dem hemmelige. Det kan de jo sagtens sige… Historien om kryptering var og er fuld af skæg og blå briller, hemmeligheder, trusler,… og kamp mellem privatliv og mulighed for at kigge “the bad guys” i kortene, Hellman beretter om sit liv i kryptering her.). Både Diffie og Hellman har været meget aktive i kampen for privatliv og også nedrustning. Her er Hellmans blogindlæg, fra i går. Han vil bruge pengene på et nedrustningsinitiativ.

Tilbage til det, de fik Turingprisen for:

Diffie og Hellman forudså i artiklen ovenfor, at man i fremtiden ville have et meget stort behov for hemmelig kommunikation: “The development of computer controlled communication networks promises effortless and inexpensive contact between people or computers on opposite sides of the world, replacing most mail and many excursions with telecommunications. For many applications these contacts must be made secure against both eavesdropping and the injection of illegitimate messages. At present, however, the solution of security problems lags well behind other areas
of communications technology. Contemporary cryptography is unable to meet the requirements, in that its use would impose such severe inconveniences on the system users, as to eliminate many of the benefits of teleprocessing.”

Og det havde de jo ret i. De forudså både behovet for kryptering med henblik på at undgå, andre læser med, og behovet for en digital signatur, så man er sikker på, beskeden kommer fra den, man tror, den er fra. Det ville ikke være smart, hvis vi skulle cykle et sted hen og hente en hemmelig nøgle, før vi kunne handle på nettet. I artiklen foreslår de den løsning, vi bruger idag, nemlig en kryptering, som er asymmetrisk: Man kan ikke udfra den nøgle, der bruges til at kryptere, gætte den, der skal bruges til at dekryptere. Eller rettere: Det skal være meget svært at gætte/regne det ud. De skriver. “In a public key cryptosystem enciphering and deciphering are governed by distinct keys, E and D, such that computing D from E is computationally infeasible (e.g., requiring 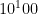 instructions). The enciphering key E can thus be publicly disclosed without compromising the deciphering key D. Each user of the network can, therefore, place his enciphering key in a public directory.”

Umiddelbart lyder det jo sært: Kryptering og dekryptering er to sider af samme sag, den ene er den inverse til den anden, så at forestille sig, at man kan kende D uden at kunne finde E på en superhurtig computer, kræver fantasi. Og matematik.

Diffie-Hellman protokol til udveksling af nøgler

I artiklen giver de en protokol  til hemmelig udveksling af nøgler over en offentlig kanal. Alice og Bob vil gerne bestemme sig til en fælles nøgle.

De vælger et (stort) primtal q (dem kan man finde ganske effektivt) og arbejder nu i det endelige legeme GF(q) med q elementer. Eksempel. q=11, som ikke er stort, men alligevel. Der er 11 elementer i GF(11) og vi kan kalde dem 0,1,2,3,…,10. Dem kan man lægge sammen og gange sammen: modulo 11. 1+3=4, som ventet, men 3+8=0 eftersom 11=1×11+0. Og 3×8=2, da 24=2×11+2 og altså giver 2, når vi dividerer med 11 og ser, hvad resten er.

Elementerne 1,2,3,4,5,6,7,8,9,10 har allesammen en multiplikativ invers, en makker man kan gange med og få 1. For eksempel er 10×10=1 modulo 11, da 100=9×11+1, så 10 er sin egen invers. Og 4×3=1, da 12=11+1. Disse 10 elementer udgør den multiplikative gruppe i GF(11)

I Diffie Hellman protokollen skal man desuden bruge et element, som frembringer den multiplikative gruppe. Altså et element, som når man ganger det med sig selv et antal gange, når rundt til alle de 10 elementer (Der er altid  q-1 elementer i den multiplikative gruppe for GF(q))

Lad os prøve med 2: , hvor vi hele tiden tager udregner rest ved division med 11. Så vi nåede gennem alle 10 elementer.

Med 3 går det ikke. og så starter man forfra.

Kun 2, 6, 7 og 8 er frembringere.

Nu tager vi et hemmeligt tal X, primtallet q og frembringeren a og udregner

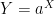 modulo q. Og fortæller hele verden, hvad Y er.

Det diskrete logaritmeproblem består i at finde X, når man kender modulo q. For et stort primtal q (og det skal mindst være større end tallet X), er dette problem vanskeligt – der er mange step i en computer.

I eksemplet ovenfor kunne vi kryptere beskeden X=6 med q=11 og a=2. Da er modulo 11. Og det har vi regnet ud ovenfor. Y=9.

Man kan få et indtryk af, at det er svært at udregne eksponenten, altså at finde X udfra Y, når man ser på udregningen  – rækkefølgen 2,4,8,5,10,9,7,3,6,1 indikerer, at det ikke er helt simpelt.

Men hvad skal Alice og Bob gøre? De kan vel heller ikke løse det diskrete logaritmeproblem. Nej, men de gør som følger: De vælger hver sit hemmelige tal n og m. Alice kende n, Bob kender m, hele verden kender q og frembringeren a (her q=11 og a=2)

Alice sender sit tal n krypteret til Bob, så Bob modtager A=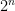 modulo 11. Bob sender sit hemmelige tal m krypteret som B= 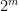modulo 11.

Nu udregner Alice 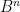modulo 11 og Bob udregner modulo 11. De har nu begge tallet 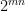modulo 11 = modulo 11, som er deres fælles hemmelige nøgle. De finder altså ikke ud af, hvad den andens hemmelige tal var, men finder en ny fælles hemmelighed.

Eksempel. n=6 og m=8. Da er A=9 og B=3. Udregner man modulo 11, får man 3 og det gør man også, hvis man udregner modulo 11. Tallet 3 er nu den hemmelige nøgle. Og den har ikke kunnet opsnappes på den kanal, Alice og Bob kommunikerer over, da det ville kræve, man kendte enten n og B eller m og A. Og kun Alice hhv Bob kender n og m.

Her er et andet eksempel:

1) Alice og Bob bliver enige om p=23, g=5 (f.eks. ved, at Alice sender de tal til Bob)
2) Alice vælger et hemmeligt tal, a=6, udregner g^a=5^6 og tager rest ved division med p=23. Det giver 8. Det tal sender hun til Bob.
3) Bob vælger sit eget hemmelige tal, b=15, udregner g^b=5^15 og resten ved division med p=23. Det giver 19, og det sender han til Alice.
4) Alice udregner nu 19^a=19^6, tager rest ved division med p=23 og får 2.
5) Bob udregner 8^15, rest ved division med p=23 og får 2.

Nu er 2 deres fælles hemmelige nøgle. Andre kender ikke a og b, så de kan ikke lave trin 4 og 5, selvom de har aflyttet det tidligere.

Man kan også bruge ideen med den diskret logaritme til at lave et public key system, men det er ikke det, der bruges mest idag.

Kryptering med offentlig nøgle.

Senere kom nemlig RSA (Rivest Shamir, Adelman) kryptering, hvor kryptering, E, bruger et produkt af to store primtal, n=pq, mens dekryptering, D,  bruger de to primtal. Udfra n kan man ikke finde p og q uden at bruge rigtig meget tid på en stor computer. Det tror vi da. Vi ved ikke, om der findes en supersmart algoritme, der kan det, men det tror vi ikke. Neil Koblitz skrev i Notices of the AMS om det problematiske forhold mellem teori og praksis i kryptering. Der kan være andre angreb end at gå direkte efter at faktorisere primtal og ofte undervurderer matematikere den praktiske side – hvad nu, hvis nogen kan få fat i de hemmelige tal af en bagvej for eksempel.

Koblittz skriver også om “The Crypto Rump Sessions“, som Diffie har ledet i de første mange år. Det er en del af konferencen Crypto og kræver underholdende indlæg; der er regler for, hvad man må kaste efter foredragsholderne. Et eksempel på et abstract: Over 3 years ago, curtains were invented with provided ‘full-window protection’. No longer could people be observed sleeping in their bedrooms from the street. Now, on behalf of crime victims the world over, we are asking whether these curtains are truly worth the cost. Curtains significantly limit our capacity to investigate these crimes and severely undermines our efficiency in the fight against terrorism. Why should we permit criminal activity to thrive behind drawn curtains, unavailable to law enforcement?….

Ja. Det kan man. Den findes allerede. Det er bogen Fermats Sidste Sætning, som er en billedbog lavet af kunstnergruppen Surrend og udgivet hos Dome of Visions. Surrendmedlem Jan Egesborg er også matematiklærer på Esbjerg Gymnasium og han har rådført sig med Johan P.Hansen, matematiker ved Århus Universitet, som har holdt en del foredrag om beviset for Fermats Sidste Sætning, FSS. (Der er noter og slides fra foredrag på siden).

Men måske er det slet ikke en børnebog om Fermats Sidste Sætning og derfor ikke et eksistensbevis? Selvfølgelig er beviset for Fermats Sidste Sætning ikke med i bogen. Det fylder godt 100 sider i Annals of Mathematics og kan end ikke læses af det store flertal af matematikere. Det kræver, at man er velbevandret i elliptiske kurver og algebraisk geometri, som er det område, beviset ligger i.

Bgoen blev anmeldt i Politiken

Jeg synes alligevel, det er en bog om Fermats Sidste Sætning. På samme måde, som børn kan lege med magneter og magnetisme, selvom magnetisme er en kvantemekanisk effekt og selvfølgelig ikke kan forstås af børn. Selvfølgelig kan børn ikke forstå beviset for Fermats sætning, men det, bogen gør, er at illustrere et modstridsargument. Der henvises på bagsiden af bogen til “Gerhard Freys smukke bidrag”. Frey konstruerede en elliptisk kurve hørende til et (muligvis ikke eksisterende) modeksempel til Fermats Sætning. Altså, hvis der findes naturlige tal a,b,c, så med n mindst 3, så findes en elliptisk kurve af en bestemt type. (Den er “ikke modulær”). Den kaldes en Frey-kurve.

Frey-kurven er en elliptisk kurve, hvis vi laver den udfra et modeksempel til FSS og den er “ikke modulær”. Det fører alt for vidt at definere elliptiske kurver – men i første omgang er det en kubisk kurve – ligningen er et polynomium i x og y og graden er 3. Man får et -led og ikke højere. Løsningsmængden (med x og y reelle tal) er en delmængde af planen – figurerne nedenfor er eksempler på kubiske og faktisk elliptiske kurver, taget fra Mathworld. Elliptiske kurver har en sammenhæng med komplekse funktioner, som er dobbeltperiodiske – der findes to komplekse tal , sådan at   for alle hele tal  . De to tal  må ikke opfylde hvor c er et reelt tal (eller omvendt – de er lineært uafhængige over de reelle tal), så punkterne  giver et gitter i den komplekse plan. funktionen f er altså bestemt ved sine værdier i et parallellogram og værdierne matcher langs kanterne. Folder man parallelogrammet sammen langs modstående kanter, får man en torus, så f er en funktion på en torus.

Elliptiske kurver fra Eric Wessteins Mathworld. Det får sort baggrund, hvilket formentlig kunne editeres værk, men I får lov at abstrahere i stedet for.

Frey indså, at hvis Taniyama Shimura Weil- formodningen er korrekt,  så findes der ikke nogen Frey-kurver. Fordi alle elliptiske kurver over de rationale tal ifølge Taniyama Shimura Weil  er modulære. Frey kunne ikke selv bevise dette, selvom han gav en del afargumenterne, så det tog flere matematikeres arbejde at få lukket hullet. Jean-Pierre Serre og Ken Ribet, nærmere bestemt. Da så Andrew Wiles beviste Taniyama-Shimura-Weil-formodningen, kunne han henvise til Frey, Serre og Ribet og konkludere, at Fermats Sidste Sætning er korrekt. Bemærk, at billedet af beviset for FSS som én matematikers arbejde – “the mathematical Marlboro Man” ikke er rigtigt.

I billedbogen indgår sådan en modstrid: Hvis der er en løsning, så er der et objekt (jeg vil ikke afsløre, hvad det er for et – I må jo låne bogen på biblioteket eller købe den), som man (tudsen på bogens forside) kan konkludere ikke findes. Jeg synes, det bliver lidt svært at være overbevist, når man tegner dette objekt – for så er det der jo allerede i en helt anden fysisk form end et abstrakt matematisk objekt såsom en løsning til FSS og en ikke-modulær elliptisk kurve – men det er rigtig fint at fortælle, at matematik indeholder den slags argumenter. Og forældre burde tale med børn om logiske slutninger og fejlslutninger. Der er nok af eksempler i hverdagen!

Der er mange andre aspekter af matricer, vektorer, produkt af matricer etc. end det, der ligger først for, nemlig løsning af lineære ligningssystemer. I et tidligere blogindlæg så vi på en ret lavtflyvende anvendelse, nemlig ideen om, at tal stillet op i et rektangulært skema, kan repræsentere billeder. Der kom lineær algebra ikke alvorligt i spil. Her tager vi, igen med udgangspunkt i bogen When Life is Linear: From Computer Science to Bracketology,  fat i matrix-vektorprodukt, egenvektorer og hvad det mon har med grafer at gøre. (Og hvad en graf er…).

Her er igen en matrix og en vektor .

Man kan gange en matrix med en vektor og få en ny vektor. En matrix med m rækker og n søjler kan ganges med en vektor med n koordinater og giver så en vektor med m koordinater. Matricen og vektoren ovenfor kan altså ganges sammen. Resultatet er en vektor med 3 koordinater. Det giver en funktion, som tager en vektor med n koordinater ind og giver en med m koordinater ud – fra til og går som følger:

1) Tag skalarproduktet af første række i matricen med vektoren v. Det giver . Det er første koordinat i vektoren . Og nej, det er ikke kønt, man man kan se, hvad der ganges med hvad.

2) Anden koordinat fås ved skalarprodukt af anden række i A med v etc.

Hvis matricen B er kvadratisk, altså har lige mange søjler og rækker, så har produktet Bw lige så mange koordinater som w.

Her er en kvadratisk matrix   Den er endda symmetrisk – hvis man spejler den i den diagonal, der går fra nordvest til sydøst, får man samme matrix tilbage. Det er nabomatricen for grafen  her. I den første række står 1 i søjle 2 og 5, fordi knude nummer 1 er forbundet til knuderne 2 og 5. Og så fremdeles. Bliver man mon klogere af at opstille nabomatricen? Ja, det gør man. Ganger man B med sig selv (se mine Pencasts, 1 og 2 om hvordan man gør det.) får man matricen , som indeholder information om, hvor mange stier af længde to, der er mellem knuderne. Eksempelvis er indgangen i 2.række, fjerde søjle skalarprodukt af anden række i B, som er (1,0,1,0,1,0),  med fjerde søjle i B, som er (0,0,1,0,1,1). Det tæller sammen, hvor mange steder 1-tallerne matcher. Det gør de på 3. og 5. koordinat. Så der er en sti fra knude 2 til knude 4 via knude 3 og en via knude 5.  Den første række (og første søjle) fortæller, hvor mange stier af længde 2, der er fra knude 1. Der er 2 stier fra 1 tilbage til 1, nemlig 1 til 5 til 1 og 1 til 2 til 1. Der er en sti til knuden 2, nemlig 1 til 5 til 2. og tilsvarende for knuderne 3, 4 og 5. Man kan ikke komme til 6 i to skridt, så der står 0. Nu kan læseren nok forudse, hvad der sker, hvis vi udregner etc. Men det gør jeg ikke her.

Der er andre matricer hørende til en graf: Et eksempel er Laplacematricen:  I diagonalen står antal af kanter, der udgår fra den tilsvarende knude, så der står 2,3,2,3,3,1, fordi eksempelvis knude 5 er forbundet til 3 andre, mens nummer 6 kun er forbundet til en anden. Udenfor diagonalen står , indgangene i B med negativt fortegn.

Summerer man elementerne i en given række eller søjle, får man 0 (tænk over det – det er ikke svært). Så matrix-vektorproduktet , hvor v=(1,1,1,1,1,1),  giver 0-vektoren.

Vektoren v er altså en egenvektor for matricen L(B) med tilhørende egenværdi 0. For en kvadratisk matrix A er w en egenvektor med tilhørende egenværdi s, hvis Aw=sw og hvis w ikke er 0-vektoren (det ville være snyd…). Altså hvis effekten af at gange w med A blot er at strække eller skrumpe vektoren w med faktoren s.

Vi har set, at L(B) har 0 som egenværdi med vektoren (1,1,1,1,1,1) som tilhørende egenvektor. Det siger ikke noget om grafen, for det er altid sådan for Laplacematricen hørende til en graf. Alle vektorer (k,k,k,k,k,k,k) er egenvektorer hørende til egenværdien 0. Men der er information at hente i de “næste” egenværdier/egenvektorer:

1. Alle egenværdierne er ikke-negative.
2. Egenværdien 0 har geometrisk multiplicitet 2 (der er andre egenvektorer end blot (k,k,k,k,k,k,k)) hvis og kun hvis grafen ikke er sammenhængende. Det er ret let at se, at det gælder den ene vej: Hvis grafen ikke er sammenhængende kan man omnummerere hjørnerne, så de første udgør en sammenhængende del og de sidste en anden. Laplacematricen bliver da blokdiagonal: Med seks hjørner, hvor de fire første hænger sammen og de sidste to hænger sammen får man og vektoren (1,1,1,1,-1,-1) er en egenvektor hørende til egenværdien 0 (fordi begge hjørnematricer er Laplacematricer.) Hvis der er k sammenhængskomponenter, er der k lineært uafhængige egenvektorer hørende til egenværdien 0.
3. Der er også information i egenvektoren/egenvektorerne hørende til den næstmindste egenværdi: Den kaldes Fiedlervektoren og siger, sammen med størrelsen af den næstmindste egenværdi noget om “hvor godt” dele af matricen hænger sammen. Fjerner man nogle kanter, bliver den næstmindste egenværdi mindre. I eksemplet får vi egenvektoren <0.415, 0.309, 0.069, −0.221, 0.221, −0.794> og egenværdi 0,723 (afrundet). Der er fire positive koordinater, nummer 1,2,3,5 og to negative, 4 og 6. De tilsvarende knuder i grafen hører sammen – 6 sidder ude for sig selv og kun fast i 4. Og de to dele er sammenhængende. For en fuldstændig graf, hvor alle knuder er forbundet med alle andre, har Laplacematricen to egenværdier, nemlig 0 og antal knuder, n. Så den næstmindste er antallet af knuder. Den har n-1 lineært uafhængige egenvektorer af typen (-1,0,0,…,1,0,…,0) Altså -1 i første koordinaten, 0 alle andre steder undtage et sted, hvor der står 1. Den næstmindste egenværdi er altså højst n og i så fald er grafen så sammenhængende, som den kan blive.

Spektral grafteori drejer sig om egenværdier og egenvektorer for matricer, der hører sammen med grafer, såsom nabomatricen og Laplacematricen. Der er forbindelser til netværk af elektriske modstande, til tilnærmelser af funktioner,… Se for eksempel Daniel A Spielmans  noter. Det er meget smukt og smart. Og som tidligere gælder det om at forstå graferne og matricerne på flere måder: Hvad er den lineære funktion svarende til nabomatricen? Hvordan kan man “se” den på grafen? Hvad med Laplacematricen?  Fun fact: For en vektor v=(v1,v2,…,vn) og en Laplacematrix for en graf, er summen af alle de differenser , hvor det i’te og j’te hjørne er forbundet med en kant. I eksemplet ovenfor, ville man få . For en fuldstændig graf får man alle

Grafer bruges som modeller mange steder, og der er en stor interesse i eksempelvis algoritmer, der finder længste/korteste vej, centralitet (hvilke knuder er centrale, så man skal igennem dem næsten uanset, hvor man kommer fra og til) og meget mere. Der er netværk af Facebookvenner, af www-sider, af neuroner i hjernen, af byer via veje, via flyruter, via jernbane,…

Titlen er fra bogen “When life is Linear – from computer graphics to bracketology.” af Tim Chartier. Det er en rigtig fin bog, som jeg fik anbefalet af Arne Jensen. Chartier har holdt foredtag på MOMath, Museum of Mathematics i New York og det er heldigvis på YouTube:

Lineær algebra er en fundamental del af enhver uddannelse i retning af ingeniørvidenskab, naturvidenskab, oecon,..  I gymnasierne er lineær algebra vektorer, skalarprodukter, krydsprodukter og naturligvis lineære funktioner f(x)=ax+b. Tim Chartier giver en lang række eksempler på, hvordan ideerne fra lineær algebra kan udnyttes – fra, som titlen siger, computergrafik til “bracketology” (parantesologi kunne det hedde), som drejer sig om at lave sportsturneringer, som matcher de rette hold. Bogen fokuserer på datamining og computergrafik. I denne blogpost får I kun en lille forsmag, men jeg vil give flere eksempler fra bogen senere.

De fundamentale objekter i lineær algebra er vektorer og matricer:

Her er en matrix og her en vektor

En matrix er et skema med tal – den ovenfor er en 3×4 matrix, 3 rækker, 4 søjler. En vektor er en matrix, som kun har én søjle (eller kun én række). Så det er jo nemt nok. Tal stillet op i sådan et skema kunne for eksempel repræsentere pixels i et billede. Hvert tal er så gråtonen for netop den pixel. Et farvebillede kan have tre tal for hver pixel – så får matricen tre gange så mange søjler (eller rækker, hvis man skriver dem på den led). Billedmanipulation er nu matematiske operationer på matricen. Her er Mona Lisa. Hun har rød, grøn, blå værdier for hver pixel. Værdierne ligger mellem 0 og 255.

Hun er altså en kæmpestor matrix. Eller man kunne sige, hun er tre matricer, en for hver af de tre farver. Hvis jeg vil have et “negativ”, kan jeg tage alle pixelværdier, gange dem med -1 og lægge 255 til.

Det har jeg gjort. nedenfor, (på dette websted, Tim Chartiers college, hvor man kan lege mere med billedet af Mona Lisa, eller selv uploade et billede) hvor man også kan se resultatet af kun at “invertere” en af farverne. Altså eksempelvis at få meget blå, hvor der før var meget lidt og omvendt.

Blå pixels omvendt

Alle pixels omvendt

Grønne pixels omvendt

Røde pixels omvendt.

Pointen er, at man ved at repræsentere billedet som matematik, åbner for en stribe muligheder. På siden ovenfor kan man mere generelt lave manipulationer af typen mx+b, hvor x er pixelværdien og man kan vælge m og b. Inversion, som jeg har lavet ovenfor, er -x+255, altså m=-1 og b=255.

Men der er meget mere matematik at hente i lineær algebra end at gange alle indgange i en matrix med et tal og derefter lægge et andet tal til, selvom det alene giver mange muligheder. I bogen kan man læse om (meget simpel) “edge detection”, hvor man erstatter (gråtone) pixelværdien p(i,j) i indgang (i,j) i’te række j’te søjle med p(i,j-1)+p(i,j+1)-2p(i,j), altså summen af pixels lige ovenfor og nedenfor  minus 2 gange den oprindelige pixelværdi (det er den diskrete anden afledte). Hvis de tre pixelværdier er ens, får man 0, altså sort. Det gør man også, hvis der er en lineær sammenhæng: p(i,x)=ax+b giver a(j-1)+b+a(j+1)+b-2(aj+b)=0. Alle områder med konstant farve bliver sorte – de får værdi 0. Lad os tage et simpelt eksempel, en oktagon, som er repræsenteret af matricen

Bruger vi nu metoden ovenfor og lader kant-pixels være sorte, får vi 

Bemærk, hvordan den lodrette kant forsvinder – alt med konstant farve bliver 0 og den horisontale og delvis den skrå er fremhævet. Mere indviklede metoder laver andre kombinationer af nabopixels for at finde andre effekter. Det snyder, at jeg kun bruge 0 og 1, men ideen fremgår forhåbentlig.

I får ikke mere denne gang – men så har I noget at glæde jer til. Vi har slet, slet ikke brugt styrken i lineær algebra endnu.

Dette forår er AAUs matematikere usædvanligt aktive i Ungdommens Naturvidenskabelige Forening i Aalborg. Så der kan I “se giraffen/girafferne”. Mange gymnasier har en aftale med UNF om gratis adgang. I kan også komme til åbent hus, hvor det nu mere er de studerende, I møder, eller I kan blive “studerende for en dag” eller meget andet.

Tirsdag 16. februar er emnet i UNF Aalborg Matematikkens Store Uløste Problemer.

Matematikken vokser hele tiden. Nye resultater bevises, formodninger afkræftes, nye teorier udvikles. Der er formodninger, som matematikerne har forsøgt at bevise eller modbevise i flere hundrede år. Mest kendt er nok Fermats sætning, men i de senere år er der kommet nye resultater om både primtalspar, Goldbachformodningen og Poincareformodningen. Foredraget vil give eksempler på disse og andre store uløste problemer og lidt om, hvad de nyere resultater siger. Også de syv milleniumproblemer vil blive omtalt. Fokus vil være på de problemer, der handler om tallene, primtal eksempelvis. Dem kan man forholdsvis let forklare. Selvom vi ikke kan løse dem. Det er mig, der holder foredraget.

Tirsdag 29 marts er emnet Ruter i Netværk.
Et netværk (eller en graf) består af et antal knuder og et antal kanter, der hver forbinder to knuder. Kanterne kan eventuelt have en retning. Vejnettet i Danmark er et eksempel på et netværk, hvor knuderne svarer til vejkryds og en kant er en vejstrækning mellem to kryds. Men der findes også mere abstrakte netværk, som f.eks.: opførelse af en bygning kan inddeles et antal aktiviteter, som hver repræsenteres af en knude; en kant med retning fra knude A til knude B kan angive at aktiviteten A skal udføres før B.

Man er tit interesseret i at finde en rute fra knude A til knude B, hvor man altså går fra A til B langs med en række kanter. Man vil helst finde den kortest mulige rute.

Vi vil se på algoritmer, der kan finde en sådan kortest rute. Og vi vil overveje om algoritmerne er tilstrækkeligt hurtige til at finde korteste veje i store netværk.

Vi vil desuden se overraskende eksempler på anvendelser af korteste ruter i mere abstrakte netværk. Foredraget holdes af Leif Kjær Jørgensen.

Torsdag 31.marts kan I høre om Uendelighed.

Uendeligheds konceptet er blandt de få matematiske redskaber som er meget vigtige til forståelsen af en bred vifte af andre (ikke nødvendigvis matematiske) begreber. Til at gøre tingene mere komplicerede, så findes der uendeligt mange typer af uendelighed, en mere uendelig end den anden!

Vi skal starte med at definere de endelige og de tællelige mængder, og vi skal fortsætte med konstruktionen af de reelle tal som uendelige decimalbrøker. Vi skal bruge Cantors diagonalargument til at bevise, at de irrationelle tal ikke er tællelige. I pausen skal vi drikke en kop kaffe i Hilberts Hotel.

Hvis alt går godt så når vi til at snakke lidt mere generelt om mængdesammenligning, kardinalitet, udvalgsaksiomet og Banach-Tarskis paradoks.Det er Horia Cornean, der er foredragsholderen.

Bor du tættere på Odense, Århus eller København, så kan du også finde UNF-foredrag der.

I sidste uge skrev jeg (og især Horia) om Cantormængden. Der var et argument for, at Cantormængden har “længde” 0, fordi det, der fjernes, ialt har længde 1. Yderligere så vi, at Cantormængden er kompakt, ikke-tællelig og ikke har indre punkter. I konstruktionen af Cantormængden fjernes den midterste tredjedel af hvert tilbageværende interval, Man kunne spørge, hvad der ville ske ved “kun” at fjerne den midterste fjerdedel af hvert af de tilbageværende intervaller. Bliver der så ikke mere tilbage i den sidste ende? Svaret er, at det gør der ikke. Den samlede længde af det, der fjernes, er stadig 1. Men man kan fjerne mindre og mindre på en anden måde:

Den fede Cantormængde eller Smith-Volterra-Cantor-mængden er også ikke-tællelig, kompakt, har ingen indre punkter (den er sin egen rand), men den har længde 1/2. Den konstrueres næsten ligesom Cantormængden, men man fjerner mindre delmængder undervejs:

Start med det lukkede interval [0,1] og fjern den midterste (åbne) fjerdedel. Så har vi [0,3/8] U [5/8,1] tilbage. Nu fjerne vi den midterste sekstendedel fra hvert af de to intervaller og har så

I hvert skridt fjernes et langt stykke midt i hvert af de intervaller, der er tilbage. Ialt fjerner man for n=1,2,3,… ialt

Så det tilbageværende har længde Det er den fede (eller en af de fede) Cantormængder. Når man tænker på, at der ikke er nogen indre punkter i mængde, er det altså virkelig underligt og en lille smule rystende: Der er en total længde på , men der er ikke nogen bittesmå “rigtige” intervaller i mængden.

Argumentet for, at der ikke er nogen indre punkter er som følger. Start med et punkt p i [0,1]. Uanset hvor lillebitte et , du vælger, så er der i intervallet punkter, der bliver fjernet i processen. Så hvis p ligger i den fede (eller for den sags skyld den tynde) Cantormængde, så er der ikke mulighed for at tage med nok så lille epsilon, uden at få noget fra komplementet til Cantormængden (fed eller tynd) med.

Har man først fået ideen, kan man konstruere fede Cantormængder med andre længder. Det kan I eksempelvis læse om hos Evelyn Lamb på Scientific American. Der kan I også se, at Cantormængden (fed eller tynd) ikke er tæt uanset hvor lille et delinterval af [0,1], man vælger, så vil der i dette lillebitte interval være et delinterval, som er blevet fjernet. Ethvert punkt y i det indre af dette delinterval,  kan adskilles fra Cantormængden med som ikke indeholder noget fra Cantormængden (for lille nok . Cantormængder er intetsteds tætte. Men fylder alligevel, hvis de er fede…

For godt en uge siden, 7. januar 2016 annoncerede GIMPS, at de har fundet endnu et Mersenneprimtal, nemlig 2^74.207.281-1. Det plejer at give en avisnotits eller to, men faktisk er det ikke i sig selv særlig interessant, hvor stort det største kendte primtal er. Vi ved nemlig, og har vidst det siden Euklid, at der er uendelig mange primtal; eller sagt på en anden måde: Uanset hvor stort et tal, nogen giver mig, så ved jeg, at der er primtal, der er større end det.

Men det er da fascinerende, at man ved, at netop tallet 2^74.207.281-1 er et primtal. Det har 22.338.618 cifre i titalssystemet, så ja, det er godt nok stort.

Mersenneprimtal er primtal på formen 2^p-1, hvor p i øvrigt også er et primtal. Ellers kan 2^p-1 ikke være et primtal: Man kan nemlig faktorisere

, så hvis hverken r eller s er 1, har vi en faktorisering i ikke-trivielle faktorer.
Man kan sige mere end det, nemlig at primtal på formen altid har a=2 og p et primtal. Hvorfor? Jo, vi har lige set, at a-1 går op i (brug s=1 og r=k i formlen ovenfor, og sæt a ind i stedet for 2) og hvis a ikke er 2 giver det igen en ikke-triviel faktorisering.

Altså er 74.207.281 også et primtal.

De første Mersenneprimtal er 3 (p=2), 7 (p=3), 31 (p=5), 127 (p= 7), 8191 (p=13) og de har været kendt i mere end 500 år. På Sloanes website med lister over heltal, som Ege har skrevet om her på bloggen, kan man finde en liste over primtal, som er eksponenter i Mersenne primtal. Den er nu ikke ajourført med det seneste i skrivende stund. Da man i 1963 fandt ud af, at p=11.213 giver et Mersenneprimtal, (det er det 23. af de 49 kendte Mersenneprimtal) lavede Illinois et særligt poststempel:

(Fra Eric Weissteins Mathworld)

GIMPS-projektet, Great Internet Mersenne Prime Search begyndte i 1996 som et af de første eksempler på “crowd sourcing” hvor mange stiller deres computere til rådighed for en større opgave. Det er interessant og senere brugt mange andre steder, at man på den måde fordeler beregninger til mange; og organiseringen af, hvordan man udnytter de mange mindre computere, er en opgave i sig selv – distribuerede beregninger er et område i datalogi.

Vi ved ikke, om der findes uendelig mange Mersenneprimtal, men med det seneste har vi da fundet 49. Hvis man vil finde meget, meget store primtal, så er Mersenneprimtal imidlertid et godt bud. Det er generelt svært at teste et stort tal for, om det er et primtal – og mere generelt at faktorisere et stort tal i sine primfaktorer. Men der er en test, Lucas Lehmer testen,  som kun virker for tal på formen 2^p-1, altså potentielle Mersenneprimtal,  og som er hurtigere end andre tests for tal i den størrelse. Derfor kan det være smart at tage forholdsvis store primtal, som 74.207.281, (dem kan man finde ved en af de sædvanlige tests), og se om 2^p-1 er et primtal. Og hvorfor vil man så finde store primtal? Tjah – af nysgerrighed, for at teste sin hardware, for at finde nye algoritmer til andre ting,… på “Why do people find these big primes?” er der en liste med 7 begrundelser:

1. Tradition!
2. For the by-products of the quest
3. People collect rare and beautiful items
4. For the glory!
5. To test the hardware
6. To learn more about their distribution
7. For the money?

Jeg kan afsløre, at punkt 7 ikke er en hovedbegrundelse.

Fra Eric Weissteins Mathworld.

Om punkt 6 kan man sige, det er svært at lave formodninger, hvis man kun har 49 Mersenneprimtal, men på Mathworld er der en graf med antallet af Mersenneprimtal Mp=2^p-1 med p < ln(x)  (grafen til venstre på figuren). De finder bedste rette linje og skriver en anelse skeptisk:  “If the line is not restricted to pass through the origin, the best fit is . It has been conjectured (without any particularly strong evidence) that the constant is given by , where is the Euler-Mascheroni constant” Nu må vi se, om nummer 49 ryger langt ved siden af linjen.

Når det er sagt, så bruges store primtal til kryptering, og det er helt fundamentalt i vores brug af netbanking og i det hele taget til hemmelig  kommunikation over offentlige kanaler- Så jo, primtal er vigtige, algoritmer til at finde dem er vigtige, og ny information om primtal er altid fint.