Statens Serum Institut (SSI) har sammen med en ekspertgruppe udarbejdet flere rapporter med matematisk modellering af COVID-19 smittespredning og sygehusbelastning. I lang tid var modellerne (beregninger, kildekode og data) ikke åbne, men i starten af marts blev en del frigivet.

Torben Tvedebrink og jeg (Mikkel Meyer Andersen) har downloadet koden og data og kigget nærmere på modellen, der ligger til grund for ekspertgruppes rapport fra 16. april. (Bemærk at der også findes en nyere model, der ligger til grund for rapporten d. 6. maj, men her er data endnu ikke frigivet.) Vores nysgerrighed har givet anledning til blog-indlægget “Sensitivitet af ekspertgruppens COVID-19-modeller“.

I det undersøger vi hvor robust modellen er for visse antagelser (fx type af residualer og fordelingen af parameterne) og om hvor stor indflydelse data om antal indlagte på intensivafdeling har på modellens forudsigelser.

På Twitter har der også været interesse for vores blogindlæg. Bl.a. har folketingsmedlem Stinus Lindgreen (Radikale Venstre) vist interesse. Han har kæmpet for øget åbenhed for data og kildekode fra ekspertgruppen.

Vi håber at data for den nyeste model også snart frigives så vi også kan kigge nærmere på den.

Dette indlæg er motiveret af https://fredhohman.com/card-shuffling/.

Opdateret 24/6-2018 10:20: Links til Numb3rs-bloggen tilføjet.

Spillekort skal blandes. En gængs måde at gøre det på, er at dele kortbunken i to mindre bunker af (ca.) samme størrelse og mikse de to bunker fra bund til top. På engelsk hedder det et riffle shuffle. (Jeg kender ikke det danske navn for denne måde at blande på.) Man kan overveje hvor mange gange dette skal gøres for bunken “er godt nok blandet” (for en passende definition af det). 7 gange er tilsyneladende nok (hvis man gør det rigtigt osv.). En matematisk model for denne måde at blande på er Gilbert-Shannon-Reeds modellen. Ovre på Numb3rs-bloggen er der mere om spillekort og matematik i dette indlæg. Bemærk at videoen (“7 gange er tilsyneladende nok”) er med Persi Diaconis som også omtales i Numb3rs-indlægget.

En mere simpel måde at blande på, er at tage det øverste kort og indsætte det et tilfældigt sted i bunken. Og sådan fortsætter man. Man kan nu stille sig selv det samme spørgsmål: hvor mange gange skal man gøre dette for at kortbunken er blandet “nok” (jf. ovenfor)?

Man kan vise (se fx 7 gange er tilsyneladende nok / https://fredhohman.com/card-shuffling/), at man i gennemsnit skal gentage en sådan simpel blanding 235 gange for at kortbunken er blandet “nok”. En del af svaret er, at bunken er blandet “nok” når bundkortet (det nederste kort i bunken inden man går i gang med at blande) har nået toppen af bunken og også selv er blevet blandet (dvs. flyttet til et tilfældigt sted i bunken).

I dette indlæg skal vi se, hvordan man kan opnå viden om eksempelvis sådanne processer ved at få computeren til at simulere mange, mange af sådanne blandinger og så registrere interessante egenskaber ved hver realiserede blanding. Denne fremgangsmåde kaldes for Monte Carlo-metoder og er et kraftfuldt værktøj indenfor statistikken. Man kan med en beskrivelse af den datagenererende process finde egenskaber for processen ved at få computeren til at realisere processen mange, mange gange.

Teoretiske resultater er ekstremt vigtige af mange årsager. Men det betyder ikke, at det er den eneste måde at opnå viden om processer på. Med Monte Carlo-metoden kan man dels kontrollere de teoretiske resultater, men ofte kan man faktisk opnå resultater som kan virke umulige at opnå teoretisk.

I dette tilfælde vil vi bruge Monte Carlo-metoden til at dels at finde det gennemsnitlige antal gange man skal blande før bunken er godt nok blandet. Det kan man også relativt let finde teoretisk (se ovenfor). Men man kunne også være interesseret i at finde fraktiler i fordelingen af antal blandinger. Så kan angive, at man i 95% af tilfældene skal blande mellem L og U gange før at bunken er blandet “nok”.

Den letteste måde at lave sådanne simulationer er på computeren med en random number generator (RNG), der kan generere tilfældige tal. Ofte må man nøjes med pseudorandom number generator (PRNG), men det er som regel også tilstrækkeligt. Og så skal man bruge et interface til denne PRNG således man kan få nogle tilfældige tal i beskrivelsen af processen. Ovre på Numb3rs-bloggen er der mere om tilfældige tal i dette indlæg.

Jeg vil her bruge R, der er et helt programmeringsmiljø (inkl. programmeringssprog) hovedsageligt anvendt til statistik, big data, maskinlæring, kunstig intelligens, dataanalyse m.fl. Det er et rigtigt godt vækrtøj at have i sin værktøjskasse. Rstudio er et fint IDE (integrated development environment) til R. Nedenfor bruges R’s sample-funktion til at trække tilfældige tal.

(Helt til sidst i dette indlæg kan I finde den komplette R-kode. Nedenfor kommer koden med output.)

Først skal vi have repræsenteret kortbunken:

> # C: Clubs / klør
> # D: Diamonds / ruder
> # H: Hearts / hjerter
> # S: Spades / spar
> faces <- c("C", "D", "H", "S")
> nums <- c("A", 2:10, "J", "Q", "K")
> 
> # Vores kortbunke: CA, C2, C2, ..., CQ, CK, DA, ..., DK, ...., SK
> # Denne genereres automatisk, men man kunne også gøre det manuelt:
> # pile_init <- c("CA", "C2") # Osv.
> pile_init <- unlist(lapply(faces, function(x) paste0(x, nums)))
> 
> # De første 6 kort i bunken
> head(pile_init, n = 6)
[1] "CA" "C2" "C3" "C4" "C5" "C6"
> 
> # De sidste 6 kort i bunken
> tail(pile_init, n = 6)
[1] "S8"  "S9"  "S10" "SJ"  "SQ"  "SK" 
> 
> # Antallet af kort i bunken
> length(pile_init)
[1] 52

Det er ikke så vigtigt hvordan bunken er blandet når vi går i gang. Vi skal egentlig bare holde styr på det sidste kort som her er “SK”.

Og så går vi i gang med at simulere 1,000 kortblandinger. Hver gang registrerer vi antallet af blandinger, der blev foretaget før bunken var blandet “nok”:

> # Funktion der simulerer én blanding
> simulate_process <- function() {
+   # Vi starter med en ny bunke
+   pile <- pile_init
+   
+   # En tæller til antallet af blandinger
+   rifs <- 0
+   
+   while (TRUE) {
+     # Registrer at der nu er bladet én gang mere
+     rifs <- rifs + 1
+     
+     # Tilfældig position som topkortet skal hen til
+     top_pos <- sample(x = seq_along(pile), size = 1)
+     
+     # Med sandsynlighed 1/52 ender det igen i toppen
+     if (top_pos == 1) {
+       #pile <- pile
+     } else if (top_pos == length(pile)) {
+       # Det kan også ende i bunden
+       pile <- c(pile[-1], pile[1])
+     } else {
+       # Eller et sted midt i mellem
+       pile <- c(pile[2:top_pos], pile[1], pile[-(1:top_pos)])
+     }
+     
+     # Hvis topkortet er bundkortet; 
+     # her kunne man også have skrevet
+     #   if (pile[1] == "SK") {
+     # men dette virker også selvom man ændrer pile_init
+     if (pile[1] == pile_init[length(pile_init)]) {
+       break
+     }
+   }
+   
+   # Topkortet (der er nu er det oprindelige bundkort)
+   # skal også blandes, men vi er ligeglade med hvor det ender
+   rifs <- rifs + 1
+   
+   return(rifs)
+ }
> 
> # Indstiller PRNG til samme tilstand for at kunne reproducere resultaterne
> set.seed(1)
> 
> # Simulér processen 1,000 gange
> riffles <- replicate(1000, simulate_process())
> 
> # De første 6 blandinger:
> head(riffles, n = 6)
[1] 249 191 205 280 189 314
> 
> # Gennemsnittet af antal blandinger
> mean(riffles)
[1] 234.757

Som I kan se får vi også at der i gennemsnit skal 235 blandinger til.

Men vores simulationer gør os i stand til at finde og vise fordelingen af antal blandinger:

> # Estimer fordelingen
> rif_dens <- density(riffles)
> 
> # Equal-tailed interval (begge haler har samme sandsynlighed)
> qs <- quantile(riffles, c(0.025, 0.975))
> 
> # Find x-værdierne
> x1 <- min(which(rif_dens$x >= qs[1]))  
> x2 <- max(which(rif_dens$x <  qs[2]))
> 
> # De centrale 95%
> rif_dens$x[c(x1, x2)]
[1] 144.2375 384.8943
> 
> plot(rif_dens)
> polygon(x = c(rif_dens$x[c(x1, x1:x2, x2)]), y = c(0, rif_dens$y[x1:x2], 0), col = "gray")
> abline(v = mean(riffles), lty = 2)

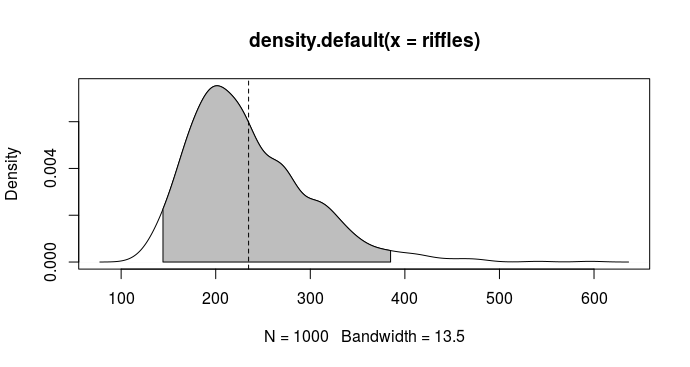
Altså vil man skulle forvente at skulle blande mellem 144 og 385 gange (og i gennemsnit 235) før at denne måde at blande på giver en bunke der er blandet nok.

(Hvilket nok er medvirkende til at jeg aldrig har set nogen praktisere denne form for kortblanding.)

Komplet R-kode:

# C: Clubs / klør
# D: Diamonds / ruder
# H: Hearts / hjerter
# S: Spades / spar
faces <- c("C", "D", "H", "S")
nums <- c("A", 2:10, "J", "Q", "K")

# Vores kortbunke: CA, C2, C2, ..., CQ, CK, DA, ..., DK, ...., SK
# Denne genereres automatisk, men man kunne også gøre det manuelt:
# pile_init <- c("CA", "C2") # Osv.
pile_init <- unlist(lapply(faces, function(x) paste0(x, nums)))

# De første 6 kort i bunken
head(pile_init, n = 6)

# De sidste 6 kort i bunken
tail(pile_init, n = 6)

# Antallet af kort i bunken
length(pile_init)

# Funktion der simulerer én blanding
simulate_process <- function() {
  # Vi starter med en ny bunke
  pile <- pile_init
  
  # En tæller til antallet af blandinger
  rifs <- 0
  
  while (TRUE) {
    # Registrer at der nu er bladet én gang mere
    rifs <- rifs + 1
    
    # Tilfældig position som topkortet skal hen til
    top_pos <- sample(x = seq_along(pile), size = 1)
    
    # Med sandsynlighed 1/52 ender det igen i toppen
    if (top_pos == 1) {
      #pile <- pile
    } else if (top_pos == length(pile)) {
      # Det kan også ende i bunden
      pile <- c(pile[-1], pile[1])
    } else {
      # Eller et sted midt i mellem
      pile <- c(pile[2:top_pos], pile[1], pile[-(1:top_pos)])
    }
    
    # Hvis topkortet er bundkortet; 
    # her kunne man også have skrevet
    #   if (pile[1] == "SK") {
    # men dette virker også selvom man ændrer pile_init
    if (pile[1] == pile_init[length(pile_init)]) {
      break
    }
  }
  
  # Topkortet (der er nu er det oprindelige bundkort)
  # skal også blandes, men vi er ligeglade med hvor det ender
  rifs <- rifs + 1
  
  return(rifs)
}

# Indstiller PRNG til samme tilstand for at kunne reproducere resultaterne
set.seed(1)

# Simulér processen 1,000 gange
riffles <- replicate(1000, simulate_process())

# De første 6 blandinger:
head(riffles, n = 6)

# Gennemsnittet af antal blandinger
mean(riffles)

# Estimer fordelingen
rif_dens <- density(riffles)

# Equal-tailed interval (begge haler har samme sandsynlighed)
qs <- quantile(riffles, c(0.025, 0.975))

# Find x-værdierne
x1 <- min(which(rif_dens$x >= qs[1]))  
x2 <- max(which(rif_dens$x <  qs[2]))

# De centrale 95%
rif_dens$x[c(x1, x2)]

plot(rif_dens)
polygon(x = c(rif_dens$x[c(x1, x1:x2, x2)]), y = c(0, rif_dens$y[x1:x2], 0), col = "gray")
abline(v = mean(riffles), lty = 2)

I dette indlæg vil jeg først vise noget grafik. Sidst i indlægget vil jeg give nogle links til nogle gode foredrag om grafik.

DR.dk bringer i dag artiklen “Ny måling: Danskerne har mest sympati med lønmodtagerne“. I den er der følgende graf:

(Kilde: DR.dk “Ny måling: Danskerne har mest sympati med lønmodtagerne“)

Min umiddelbare reaktion var: “Den graf er godt nok svær at tyde!”.

Der er flere problemer med den. For det første er cirkeldiagrammer/lagkagediagrammer svære at tyde – forstået på den måde, at det er svært at sammenligne størrelsen på de forskellige “lagkagestykker”. Hvor mange gange større er et stykke i forhold til et andet stykke? For det andet er farvevalget måske ikke velegnet til denne type graf, hvis man gerne vil bruge den til at illustrere forholdene mellem de forskellige svarmuligheder. Man kan (meget groft) dele farveskalaer op i to grupper: sekventielle (fra lyseblå til mørkeblå, fra rød til grøn osv.) eller kvalitative. De sekventielle bruges ofte til at illustrere en talværdi (fx indkomst) og de kvalitative bruges ofte til grupper (fx køn eller region).

Så alt i alt er grafen svær at tyde pga. både typen og farvevalget. Det skal dog siges, at man inde på artiklen kan køre musen over “lagkagestykkerne” for at få hjælpetekst og andelen oplyst. (Men man kan spørge om interaktivitet virkelig er nødvendig til at illustrere dette data.)

Til denne type grafer, vil man typisk anvende søjlediagrammer som fx:

Her er et par varianter. Først hvor søjlerne ordnes efter værdi:

Og vil man gerne have farver på, kan man da godt det:

Jeg vil påstå, at sådanne grafer er bedre til at hjælpe mig med at sammenligne svarmulighederne end cirkeldiagrammet er.

Det leder frem til det næste: Der er meget psykologi i grafik. Det handler ikke kun om statistik og om rent teknisk at få produceret noget grafik.

Og det er svært at lave god grafik!

Der forskes stadigvæk i, hvordan grafik tolkes – og om der er forskel mellem folkeslag. Fx er farver en oplagt del af grafik: Men man kan være farveblind og det kan man endda være på mange måder. Derfor er det vigtigt at producere grafik som også farveblinde kan læse – men det er ikke let. Og der kan muligvis også være forskel på, hvordan forskellige kulturer opfatter farver.

Auckland University (i New Zealand) har afholder hvert år en foredragsrække kaldet Ihaka lectures. Den blev første gang afholdt i 2017 og hver række består af 3 foredrag i marts måned. I år var der følgende tre foredrag:

1. “Myth busting and apophenia in data visualisation: is what you see really there?” med Dianne Cook. Link til foredraget på YouTube.
2. “Making colour accessible” med Paul Murrell. Link til foredraget på YouTube.
3. “Visual trumpery: How charts lie – and how they make us smarter” med Alberto Cairo. Link til foredraget på YouTube.

Alle disse tre foredragsholdere er kendte og gode. Jeg vil ikke bruge tid på at præsentere dem hver især her. Se i stedet deres foredrag. Men de alle illustrerer fint det sammenspil der er mellem statistik og psykologi når man laver visualiseringer/illustrationer/grafik.

Relateret til dette indlæg er måske specielt nr. 3 af Alberto Cairo. Han giver en masse gode eksempler på dårlig grafik. Ikke nødvendigvis åbenlys dårlig grafik, men grafik der kan vildlede læseren.

Di Cook (nr. 1 ovenfor) forklarer i sit foredrag også om, hvordan kan kan bruge visualiseringer til statistisk inferens i stedet for den traditionelle tilgang med hypotesetest. De har lavet forsøg med at lade folk vurdere visualiseringer, der er lavet med udgangspunkt i nulhypotesen og så se om folk kan genkende det observerede datasæt. Hvis de kan det, “stikker det ud” og kommer så måske ikke fra den model, man har specificeret i nulhypotesen. Der er muligvis nogle problemer med denne tilgang – fx er det ikke åbenlyst hvad den alternative hypotese er. Derudover er det svært at vælge teststatistik/teststørrelse (der i dette tilfælde svarer til typen af grafik brugeren skal vurdere, fx scatterplot, barplot osv.). Men det er bestemt interessant at høre om denne vinkel på statistisk inferens.

Af og til stilles der opgaver af typen “Hvad er næste tal i rækken 1, 2, 3, …?”. Her forventer spørgeren nok at få svaret 4, for spørgeren har sikkert genereret tallene ved hjælp af funktionen f(x) = x for x = 1, 2, 3, …. Lad os i stedet påstå, at svaret er 42 og argumentere hvorfor.

En måde at argumentere på, er simpelthen at give den funktion, vi påstår har genereret talrækken. Så lad os gøre det:

Lad os tjekke, at . Waw! Og så videre for 2 og 3. Prøv fx ved hjælp af Wolfram Alpha for x = 2. Og for x = 4 fås, at f(4) = 42. Endnu mere wauw.

Så svaret på opgaven, kan vi påstå er 42 lige så vel som at det burde være 4. Vi har jo på samme måde anvist et polynomium, der kan generere talrækken og næste tal er 42.

Hvordan er det polynomium så konstrueret? Det er sket ved hjælp af noget, der kaldes polynomiumsinterpolation. Det er beskrevet på blandt andet https://en.wikipedia.org/wiki/Polynomial_interpolation og der findes flere hjemmesider, der kan gøre det online, fx http://www.wolframalpha.com/input/?i=interpolating+polynomial+calculator. Polynomiet ovenfor blev fundet med dette input (klik her).

I stedet for at have påstået, at næste tal var 42, kunne vi have påstået, at det var -100. Eller 719.232. Eller at de to næste er 1 og 1. Vi ville altid være i stand til at konstruere et polynomium, der ville give præcis hvad vi ønskede.

Hvorfor kan det så lade sig gøre? Fordi der altid kan konstrueres et polynomium, hvis graf går gennem n punkter [ovenfor er det {(1, 1), (2, 2), (3, 3), (4, 42)}]. Faktisk kan det vises, at der gennem n punkter findes ét (og kun ét) polynomium af grad n-1, hvis graf går igennem præcis disse punkter. Læs mere på denne Wikipedia side: https://en.wikipedia.org/wiki/Polynomial_interpolation

Hvad gør du, næste gang du får en opgave med at gætte næste tal i talrækken?