Julenørderier.

Sidste år havde vi links til matematiske julekalendere på bloggen. I år bliver det en blandet landhandel:

Sierpinski Juletræ Fra Math Craft

Sierpinski-trekanten er en fraktal, som man næsten kan gætte definitionen af udfra juletræet. Stjernen er et Von Koch snefnug.

Egenfunktioner for Laplaceoperatoren med et juletræ som rand.

https://youtu.be/XL7xQMoouFE

Man kan tænke på det som en to-dimensional version af den svingende streng. Højere egenfunktioner svarer til overtoner.

Denne fine Møbiusjulekugle er 3d-printet. Men er man fiks på fingrene, kan man måske skære den ud af en trækugle 🙂

Møbiusbåndsjulepynt. Lavet af Teja Krasek. Jeg har lavet guirlander med Møbiusbånd i min studietid – et godt råd: Brug papir, der er farvet på begge sider…

Der er mange andre julerier derude på det store internet. Nogen hænger bogstavet $pi$ på juletræet… Skåret ud i metal eller med et antal decimaler skrevet på en julekugle. Det gør jeg ikke.

Glædelig Jul og Godt Nytår.

Uafhængighed og noget om plat og krone

Tak til Jesper Møller for ideen til følgende, som egentlig er en opgave i et kursus om Bayesiansk statistik:

Hvornår er to begivenheder/hændelser uafhængige? Det kan man få en lang filosofisk diskussion ud af, men i matematik er der en definition.

To hændelser A og B er uafhængige, hvis sandsynligheden for, at både A og B indtræffer, er produktet af sandsynligheden for A og sandsynligheden for B.

$P(A\cap B)=P(A)P(B)$

Nu slår vi plat og krone med en ærlig mønt (altså en, der giver plat med sandsynlighed 1/2 og krone med sandsynlighed 1/2 – og aldrig lander på kanten…)

Vi slår et antal gange – kald det n. Det er altså et eksperiment: Slå n gange med en ærlig mønt. (Hvis du kun har Mobile Pay, kan du slå plat og krone hos Random.org Du kan endda vælge at gøre det med danske ti-kroner)

A er hændelsen: Der optræder både plat og krone undervejs.

B er hændelsen: Plat optræder højst en gang.

Er A og B uafhængige?

De mulige udfald kan beskrives som følger/ord PPKPKKP med længde n. Der er altså $2^n$ mulige udfald af vores eksperiment.

n=1: Mulige udfald er { P, K }

n=2: Mulige udfald er { PP, PK, KP, KK}

n=3: Mulige udfald er { PPP, PPK, PKP, KPP, KKK, KKP, KPK, PKK}

n=4: {PPPP, PPPK, PPKP, PKPP, KPPP, PPKK, PKPK, KPPK, KPKP, KKPP, PKKP, KKKP, KKPK, KPKK, PKKK, KKKK}

og så orker jeg ikke lige mere, men her er fem 10-kroner, i PHPPP.

reverse obverse reverse reverse reverse

Hændelsen A sker netop, når vi ikke har slået plat i alle slag eller krone i alle slag. Så det sker i $2^n-2$ tilfælde ud af de $2^n$ mulige. Sandsynligheden er så $P(A)=(2^n-2)/2^n= 1-2^{1-n}$

Hændelsen B (højst en plat) sker, når alle n slag er krone KKKK…KK eller når der er en enkelt plat: PKKK…KKK, KPKKKK…KKK, KKPKKK…KKK etc. Der er n muligheder for en enkelt plat og 1 for ingen, så der er n+1 ialt. Vi konkluderer $P(B)=(n+1)/2^n=(n+1)2^{-n}$ .

A OG B indtræffer, hvis vi i mulighederne for B udelukker at have kun krone. Det er der sandsynlighed $P(A\cap B)=n/2^n=n\cdot 2^{-n}$ for.

Svaret på, om (eller for hvilke n) A og B er uafhængige er: Når/hvis $P(A\cap B)=P(A)P(B)$ . Altså når $n\cdot 2^{-n}=(1-2^{1-n})(n+1)2^{-n}$

Reducer ligningen – gang med $2^n$ og få $n=(1-2^{1-n})(n+1)$ udregne parenteser og reducer til $2^{n-1}=n+1$ . n=3 er en løsning og der er kun en løsning (venstresiden vokser eksponentielt og højresiden er en linje, så de skærer højst en gang).

De to hændelser er altså uafhængige, når man slår tre gange, men ikke hvis man slår flere gange eller færre!

Problemet med lykkelig slutning.

Happy Ending problemet er ikke løst, men to matematikere, Ester Klein og George Szekeres, der arbejdede med det, blev gift. Så derfor kaldte Erdös det “Happy Ending-problemet”.

Det er et af de matematiske spørgsmål, som er let at forstå, men svært at løse – tilsyneladende, eftersom det ikke er løst endnu. Og det er et af dem, der er omtalt i Popular Mechanics – ligesom Collatzformodningen, Sofaproblemet og Eulermursten, som allerede er behandlet her på bloggen.

Spørgsmålet er: Tegn punkter i planen. Der må ikke ligge tre eller flere på linje. Hvor mange skal der være for at man er sikker på at kunne tegne en konveks n-kant, hvis hjørnepunkter allesammen er nogen af dem, vi tegnede? (Konveks betyder, at randen buler udad, alle indre vinkler er højst 180 grader. Tegner man linjestykket mellem to punkter i figuren, så er det indeholdt i figuren.)

ConvexPolygon

Illustration fra MathWorld.

Hvis n=3 er det klart: Har man tre punkter, som ikke er på linje, er de hjørner i en trekant. Og trekanter er altid konvekse.

Kald antallet af punkter, der skal bruges, g(n). Vi ved nu g(3)=3.

HappyEndProblem4

Billedet fra Eric Weissteins MathWorld illustrerer, at g(4) må være større end 4. Der er vist to tilfælde, hvor man ikke kan tegne en konveks firkant. Erdös Szekeres-formodningen siger, at $g(n)=2^{n-2}+1$ . E.Klein viste, at g(4)=5 ved at bevise, at alle konfigurationer af fem punkter er en af de tre (til venstre):

HappyEndProblem

Illustrationen (igen fra MathWorld) til højre viser, at g(5)>8. Faktisk er g(5)=9. Først vist af E. Makai.

At g(6)=17 krævede computerkraft – det resultat er fra 2006.

Hvad med g(7)? Det ved vi ikke! Erdös og Szekeres viste, at g(n) er endeligt. Det overrasker muligvis ikke læseren, men hvis man ændrer problemet en anelse og spørger: Hvad er det mindste antal punkter, man skal have for at man er sikker på, der findes en konveks n-kant som ovenfor, som ikke indeholder nogen af de andre punkter (en tom konveks n-kant) så ved man, at uanset, hvor stort et N, man vælger, så kan der laves en punktmængde i planen med N punkter, som ikke indeholder nogen tom 7-kant. For en tom 6-kant gælder dette ikke, Der findes et tal, sådan at punktmængder med det antal punkter altid vil indeholde en tom 6-kant. Man ved også, at det tal er mindst 30… Se mere på Numberphile-videoen her:

Collatz-formodningen.

I får endnu et af de matematiske spørgsmål, som er lette at forstå, men indtil videre ikke har kunnet besvares.

Collatz-formodningen.

David Eisenbud forklarer Collatzformodningen. Endnu en rigtig fin video – fra Numberphile.

Collatzformodningen siger, at uanset hvilket helt positivt tal, man starter med, så ender man på et tidspunkt med tallet 1, hvis man følger proceduren og bliver ved:

Hvis n er lige, så divider med 2: n ->n/2.

Hvis n er ulige, så gang med 3 og læg 1 til: n-> 3n+1

Forfra med det nye tal.

Eksempler: Begynd med n=1. Så får man 1, 4, 2, 1. Altså tilbage igen i et lille loop.

Begynd med 9. Så får man 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

Alle de 20 tal, vi passerede for at nå fra 9 til 1 er nu undersøgt – de følger samme tur. Lad os tage et nyt: n=12. Det giver 12, 6, 3, 10 og så rammer vi et, vi har kortlagt, nemlig 10 og følger som ovenfor 10, 5, 16, 8, 4, 2, 1.

Vejen til 1 for små tal

$De første 100 tals vej ned til 1 (fra Wikipedia Creative Commons)$

De første 100 tals vej ned til 1 (fra Wikipedia Creative Commons)

Naturligvis har Sloanes heltalsfølger, som Ege Rubak har skrevet om på bloggen, forskellige varianter af spørgsmål om “3n+1”-følger, som de også kalde. Begynder man med 27 får man A008884 Listen er på 111 skridt og når helt op til 9232 på vejen.

Hvis det tal, man starter med, er mindre end 10^18, så når man til sidst 1 ved proceduren. Der er lignende problemer, som man ved er uafgørbare. Paul Erdös har efter sigende sagt, at matematikken endnu ikke er klar til at løse Collatzproblemet og Terry Tao er enig. Det er et fint problem, fordi det er let at forklare, man kan selv finde på lignende problemer – hvorfor skal der eksempelvis ganges med 3? hvad sker der, hvis man ganger med noget andet? Hvad er den længste følge af tal, man skal igennem for at nå ned til 1? Hvor langt når man op undervejs? Nok at lege med… Man kan lave heuristiske argumenter: Når n er ulige, så er 3n+1 lige, så det skridt kan erstattes med at gå til (3n+1)/2. Der er altså en omskrivning:

Hvis n er lige divideres med 2. Hvis n er ulige går man til (3n+1)/2.

Den lille analyse bruger Tao og andre til at sandsynliggøre, at man vil ende ved 1. Men det er ikke et bevis. Dog gør det, at Tao tror på formodningen…

Hvis man udvider spørgsmålet og tillader an+b i stedet for 3n+1, og desuden giver flere muligheder, a la hvis 2 går op i x, så…, hvis 3 går op i x, så…, så er spørgsmålet “vil følgen ende i 1” uafgørbart i datalogisk forstand. Det kan I læse om her http://people.cs.uchicago.edu/~simon/RES/collatz.pdf

Men man skal passe på, som xkcd bemærker:

$collatz_conjecture$

Retfærdighed og kager.

To australske dataloger har fundet en begrænset algoritme, som deler kager og andet, man vil dele, misundelsesfrit. Det skriver Erika Klarreich om i Quanta Magazine. Jeg har tidligere skrevet om den type problemer på Numb3rsbloggen, så jeg tillader mig at kopiere mig selv. Opdelinger med forskellige mål for, hvad en ideel deling er, optræder eksempelvis i økonomi – der optræder “nyttefunktioner”, som er mål for, hvor meget mere tilfreds, bestemte personer bliver, hvis de køber dette eller hint. Her deler vi kager, men I må gerne tænke på andre mere økonomiske ting – løn, ferie,…:

Kageudskæringsalgoritmer:

Det handler groft set om at dele noget – en kage eller noget andet – i et antal stykker, så alle bliver tilfredse. Et mere avanceret og kompliceret eksempel er opdeling af landområder efter en krig.

Et eksempel på en kageudskæringsalgoritme er “du deler og din søster vælger først” algoritmen, som forældre i hele verden nok kender. Ideen er, at hvis jeg deler, må jeg mene, begge stykker er lige gode. Og jeg er altså tilfreds, uanset hvilket stykke hun vælger. Omvendt er hun tilfreds, for hun får det stykke, hun selv mener ser bedst ud.

Man forestiller sig, en kage skal deles mellem personer, som har forskellige præferencer; Charlie viste en lagkage med vanille og chokolade og med glasur. Nogen sætter meget pris på glasur, andre mindre, nogen er vilde med vanille, andre med chokolade.

Vi forestiller os altså, at et stykke af kagen kan have forskellig værdi for forskellige personer. Og hele kagen kan være mere værd for en person end for en anden. Lad os sige, der er n personer, der skal dele kagen.

Man kan stille mange forskellige krav til en deling – hvad betyder det, at den er rimelig. Det kunne være

1) Proportionalt – hver person mener, at værdien af deres eget stykke er mindst 1/n af den samlede værdi. (OBS. Hvis nu jeg bedst kan lide vanilje og min søster chokolade og kagen består af halvt af hver, kan vi begge to få mere end halvdelen af det, vi mener er den samlede værdi. Ved at lade mig få den halvdel, der er vanilje og hun får den anden.)

2) Misundelsesfrit: Hver person mener, hun har fået det bedste af de stykker, kagen er delt i. (Ikke en skarp ulighed – det er nok, at der ikke er et andet, hun hellere vil have.)

3) Pareto optimalt:Vi har en opdeling, hvor enhver anden opdeling, hvor en deltager får mere, vil medføre, at en eller flere får mindre. Begrebet er en slags stabilitet overfor ændringer og optræder ofte i økonomi. Hvis jeg skal overbevise de andre om at lave det om, skal jeg overtale en deltager til at få mindre. (Det er det, der starter krige)

4) Ligeligt: Alles stykker har samme værdi. Så værdien af mit stykke for mig, er det samme som værdien af min søsters stykke for hende. Det kræver, at man kender alle deltagernes værdisætning af kagen.

Lad os begynde med to personer, som har et snit til at dele kagen. Vi vil ikke have en deling, hvor man tillader så mange stykker, at det ender med, at hver får en bunke krummer. Med “du deler, din søster vælger” algoritmen bliver delingen proportional og misundelsesfri men ikke nødvendigvis ligelig og pareto optimal.

Eksempel: Halvdelen af kagen er vanilje, halvdelen chokolade. Jeg er vild med chokolade, min søster med vanilje. jeg skærer og ved ikke, at min søster helst vil have vanilje. Så for en sikkerhedsskyld deler jeg, så begge stykker har halvt chokolade og halvt vanilje. Vi ville begge to have foretrukket delingen hvor jeg fik kun chokolade, og min søster kun vanilje – det er altså ikke pareto optimalt.

Lad os kigge nærmere på betingelserne ligelig og misundelsesfri. Pareto optimal er en lidt pudsig betingelse her, for hvis jeg får det hele, kan min søster ikke forbedre sin situation, uden jeg får mindre, end jeg havde; det er altså Pareto optimalt – og nok er jeg storesøster, men mon ikke FN eller forældre ville gribe ind.

Ligelig opdeling giver kun mening, hvis alle deltagere har samme samlede værdi af kagen, og man antager også, at alle sætter værdien af nok så små stykker højere end 0. Hellere chokolade end slet ingen kage. Lad os sige, den samlede værdi er 1.

En yderligere forsimpling er, at man kun må skære i en på forhånd valgt retning ( Tænk på en langstrakt skærekage, hvor man skærer på tværs – ikke noget med kagemænd, hvor man kan foretrække en af fødderne).

Vi kalder midtpunktet af kagen 1/2 og siger, man kan skære i punkter fra 0 til 1 (kagen er 1 lang). Fra 0 til 1/2 er der chokolade og fra 1/2 til 1 er der vanilje. (Vi antager, at stykker med areal 0, ikke har nogen værd, så det er ligemeget, hvad der er i 1/2.)

Hvis nu A er dobbelt så vild med chokolade som med vanilje, er hans værdisætning 4/3⋅x for et stykke af længde x med chokolade. Den er 2/3⋅ x for et stykke med vanilje. Vi antager, B har det omvendt.

Hvis A skal dele, vil hans strategi være, at det stykke, han ender med, har værdi mindst 1/2. (En minimax strategi – man satser ikke, men sørger for, at få mest muligt ud af det værste, der vil kunne ske.)

Så han deler i punktet p=3/8. Han har kun chokolade på stykket til venstre for p, så det har værdi

3/8 ⋅ 4/3 = 1/2

B vil vælge stykket til højre og få en værdi på 3/4, så det er ikke ligeligt, og A har snydt sig selv.

Havde A delt i midten, ville B stadig vælge stykket til højre, begge ville få værdi 2/3, og det ville være ligeligt og misundelsesfrit.

For n = 3 eller flere, kan man vise, at der findes situationer, hvor man ikke med n-1 snit kan lave en misundelsesfri og ligelig deling. Se f.eks. Better ways to cut a cake S. Brams, M.A. Jones og C. Klamler, Notices of the AMS, Vol 53 no. 11. Husk, hvis du går igang med den, at det handler om strategier og algoritmer: Hvordan ser det ud, hvis A ikke er ærlig om sin værdifunktion; er der en udenforstående involveret (FN eller andre) etc.

I How to cut a cake fairly, Walter Stromquist, American Mathematical Monthly, Vol 87, No.8, Oct. 1980, pp 640-644 (findes på Jstor for dem, der har adgang til det), bevises, at der eksisterer en misundelsesfri opdeling med n-1 snit for n deltagere. Men der er ikke en algoritme til at finde den. Det er et meget smukt argument (jo, det er det altså).
En opdeling i n+1 stykker betragtes som en stribe snit x1,x2,…,xn hvor 0 ≤ x1 ≤ x2 … ≤ xn ≤ 1. Det er de steder i intervallet mellem 0 og 1, hvor der skæres. Det tænker man så på som et punkt (x1,x2,…,xn) i et n-dimensionalt rum.
Las os begrænse os til at dele i tre stykker. Punkterne (x1,x2) vil ligge i en trekant i planen med hjørner (0,0), (0,1) og (1,1). Så hvert punkt svarer til en opdeling.
Hjørnepunkterne svarer til, at der to “stykker” uden noget, og et stykke, der er hele kagen. Kald de tre stykker, der kommer ud af opdelingen for nummer 1, 2 og 3 for stykket mellem 0 og x1, mellem x1 og x2 og mellem x2 og 1. Så er (0,0) der, hvor stykke 3 udgør hele kagen. (0,1) er, hvor stykke 2 er hele kagen og i (1,1) er det stykke 3, der er det hele.
På kanten mellem (0,0) og (0,1) er stykke nummer 1 “tomt”, og tilsvarende på de andre kanter.
I et punkt (x1,x2) vil spiller A måske foretrække stykke nummer 1, spiller B nummer 2 og spiller C måske også nummer 1. Der vil være en del af trekanten, hvori A vil foretrække 1, en anden del, hvor A foretrækker 2, og en tredie, hvor han foretrækker 3. (og nogen grænseområder, hvor han er ligeglad). Og tilsvarende for spillerne B og C. Nu skal man vise, at der findes et punkt, hvor spillerne foretrækker hver sit stykke. Og det kan man – med visse forudsætninger, men sådan er det jo i matematik. Ingrediensen i beviset er Brouwers fikspunktsætning, som har forbavsende mange anvendelser. Den siger:
En kontinuert afbildning fra en kugle til en kugle (tænk her på en klump modellervoks, som man kun må ælte og ikke flå) har et fikspunkt. (Et punkt er kommet tilbage, hvor det var)
Som illustration: Hvis man tager en blok papir, tager det øverste stykke af og krøller det sammen og lægger papirkuglen ovenpå blokken. Så vil der være et punkt, der ligger lige præcis lodret over der, hvor det var, før vi rev papiret af blokken.
Jeg vil ikke gengive, hvordan det bliver brugt i kageudskærings eksistensbeviset, men det står i artiklen.

Bemærk i øvrigt, problemet kan vendes om, så man skal dele noget, man ikke bryder sig om. Opvask og lignende. Det giver tilsvarende udskæringsalgoritmer “med modsat fortegn” i en vis forstand.

Hvad er det nye?

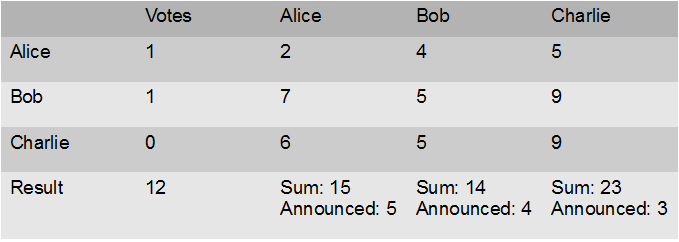
De to australiere har lavet en algoritme, som deler misundelsesfrit i endelig mange skridt. Er man kun 2, vil du deler, din søster vælger, være misundelsesfri. Men er man flere om det, bliver det mere vanskeligt, for den, der vælger sidst, kunne jo misunde en af dem, der valgte først. Den nye algoritme gør, for tilfældet med 3 personer, A,B, C følgende:

C deler i tre dele, X,Y,Z og A og B peger på det stykke, de helst vil have. Er det to forskellige stykker, er alt fint og C får det sidste.

Peger A og B på samme stykke, Z, sker følgende: B skærer så meget af dette stykke, at det, der er tilbage, Z’ er lige så meget værd – for hende! – som det, hun næsthelst ville have – lad os sige Y.

Læg det, der er skåret af til side. Lad A vælge. Hvis A ikke vælger Z’, er B tvunget til at tage det stykke. Vi har nu en misundelsesfri deling af kagen, bortset fra det, vi har lagt til side: A er tilfreds, da hun vælger først. B er tilfreds, da de to stykker, var lige meget værd. C er tilfreds, da de tre oprindelige stykker var lige meget værd. Vi har nu fordelt C fik X, B fik Y og A fik Z’ hvis ikke B blev tvunget til at tage Z’

Nu skal det afskårne deles (eller gives til hunden). Hvis A tog det tilrettede stykke, går det som følger:

B deler i tre dele. A vælger først, derefter C og til sidst B. Det er nu alt i alt misundelsesfrit. C har allerede fået X, der er lige så meget værd som Y og Z og derfor også lige så meget værd som Z’+det stykke A har fået i anden omgang. Derfor er C ikke misundelig på A. Og C vælger før B og er heller ikke misundelig på hende. B delte og er derfor tilfreds. A valgte først og er derfor glad. (Jeg indser nu, at det nok kan skrives smukt ned med uligheder mellem de forskelliges præferencefunktioner, men det kan I selv filosofere over.)

For flere “spillere”, bliver det en meget lang proces, hvor der skal byttes om på, hvem der vælger, tages hensyn til, om en delmængde af spillerne alle foretrækker samme stykke…

Sofakonstanten og Euler-mursten.

Mange store uløste matematiske problemer er meget svære at forstå. De drejer sig om matematik, som i sig selv er svært tilgængelig. Fermats problem er let at forstå. Men løsningen kan de færreste læse og forstå.

i denne uge har Popular Mechanics fem eksempler på problemer, som kan forklares, selvom vi ikke kan løse dem. Endnu. Det har jeg ladet mig inspirere af. I får to af problemerne her. Så må de andre komme senere – Cliff hanger…:

Om Euler-mursten og et problem, der ligner Fermat:

En Euler-mursten er en kasse, som opfylder

Længde, bredde og højde er hele tal. a,b,c.
Diagonalerne på sidefladerne er hele tal.

M.a.o. er a,b,c hele tal og det er løsningerne d,e, f til $a^2+ b^2= d^2$ , $a^2+ c^2=e^2$ og $b^2+ c^2 = f^2$ også.

Der er uendelig mange tripler a,b,c, som er sidelængder i en Euler-mursten. Det mindste tripel er (a,b,c)= (44,117,240). Diagonalerne har da længde 125,244,267.

$Euler-mursten. Fra Wikipedia.$

Euler-mursten. Fra Wikipedia.

Når først, man har en løsning, kan man skalere med et helt tal og få endnu en. Derfor har vi allerede nu uendelig mange. Se Wikipedia for mange andre facts om Euler-mursten. Euler fandt to uendelige familier – som ikke bare var lavet ved skalering.

Nå, men det er tydeligvis ikke et uløst problem at finde Eulermursten. Men perfekte/fuldkomne Eulermursten har vi ikke fundet nogen af.

En Eulermursten er perfekt, hvis den opfylder betingelserne ovenfor. Og dens hoveddiagonal også har heltallig længde. Altså

3) $a^2+b^2+c^2=g^2$ og g er et helt tal.

VI ved ikke, om der findes perfekte Eulermursten. Vi har hverken dundet nogen eller vist, de ikke findes. Naturligvis ved vi, at der ikke findes nogen med små sidelængder. Det kan man sætte en computer til. Hvis der findes perfekte Eulermursten, er en af sidelængderne mindst $10^12$ (påstår Wikipedia).

OBS. Den skal BÅDE have heltallige sidediagonaler (d,e,f ovenfor) OG heltallig hoveddiagonal. I Popular Mechanics påstås, at vi ikke ved, om der finde heltallige løsninger til 3) I så fald skal jeg have skrevet en artikel om, at $1^2+2^2+2^2=3^2$ . Men det tror jeg nu alligevel ikke, jeg skal…

Sofakonstanten.

For en del år siden arbejdede projektgrupperne på 1.semester med “klaverflytning”. ( Som jeg husker det, var det Hans Huttels ide.) Hvor stort et klaver kan man få igennem en smal gang, der knækker? Det kom der fine projekter ud af – de fleste fokuserede på det plane problem, hvor man skubber klaveret rundt uden at måtte dreje det undervejs, de så på idealiserede klaverer – trekantede, kvadratiske, rektangulære,…

Leo Moser er efter sigende ophavsmand til Sofaflytningsproblemet: Hvad er det største areal, en plan figur kan have, hvis den skal kunne skubbes gennem en gang med bredde 1 og et 90 graders knæk. ( Det er underforstået, at gangen er lang på begge sider af knækket og at figuren er stiv.) Dette største areal kaldes sofakonstanten.

Jopseph L. Gervers sofa (fra 1991 – artiklen er her ) er bygget af 18 kurvestykker – antydet på figuren. Den har det største areal af alle de sofaer, vi kender, som kan skubbes gennem en gang som ovenfor.

$Gervers Sofa.$

Gervers Sofa.

Arealet af Gervers Sofa er ca. 2,2195. Det præcise tal og integralet, der regner det ud, kan man finde på MathWorld og i artiklen ovenfor. VI ved altså, at sofakonstanten er større end eller lig med arealet af Gervers sofa.

Gervers Sofa. Fra Dan Romik på UC Davis. Der er flere animationer og mere om sofaproblemet.

Mange matematiske geometriske problemer har “pæne” løsninger. Et område i planen, som kan hegnes ind af et hegn med længde L har størst areal, hvis det er en cirkel. Det tilsvarende problem i rummet giver en kugleflade. Så vi bliver lidt skuffede, når der er grimme løsninger. Og Gervers sofa er grim… 18 randkurver, hvor 3 er linjestykker og resten er løsninger til nogle differentialligninger, han opstiller. Det er ikke kønt. Før Gerver, havde vi Hammersleys sofaer:

$Hammesleys Sofa. Fra Dan Romik.$

Hammersleys Sofa. Fra Dan Romik.

Hammersleys sofaer har, som man kan se, en halvcirkel i midten, to kvarte cirkler som en del af sofaryggen og linjestykker for resten. HAn konstruerede dem ved at lave en halvcirkel med radius 1 og sætte et rektangel ind i midten – det skal der så klippes en mindre halvcirkel ud af, hvis det hele skal kunne skubbes om hjørnet. Hammersley viste, at den facon er optimal, hvis den midterste halvcirkel, som er klippet ud, har radius $2/\pi$ . Det er egentlig en meget smukkere konstruktion end Gervers. Men arealet er $2/\pi+\pi/2$ altså ca. 2,2074. Hammersley fandt også en øvre grænse for sofakonstanten på $2\sqrt{2}$ (ca. 2,82). Jeg har ikke læst argumentet for det, så det vil jeg ikke udbrede mig om, men interesserede kan som altid Google.

Uanset, om den er grim vil det give ny indsigt, hvis Gervers sofa faktisk er optimal. Differentialligningerne, der indgår i hans konstruktion bygger på antagelser om en form for stabilitet af den måde, man skubber sofaen igennem. Måske er der ny viden at hente i disse antagelser.

Senere får I noget om Collatz-formodningen og den lykkelige slutning. Og måske også noget om indskrevne kvadrater.

Den matematiske version af Hønen og Ægget.

Horia har heldigvis skrevet til bloggen igen:

Den matematiske version af Hvem kom først, hønen eller ægget?

Når man første gang lærer om funktioner og deres grafer, er et koordinatsystem den første ting man tegner. Vi vælger et origo, vi tegner x-aksen, og bagefter y-aksen. Men hvor ved vi fra, at “den rigtige” y-akse skal stå vinkelret pa x-aksen? Hvorfor skal der
være $90^{\circ}$ mellem de to linjer? Og hvad har det med $\pi/2$ at gøre?
Jeg skal nu prøve at overbevise jer om, at tallet $\pi$ samt sinus og cosinus
funktionerne kom før koordinatsystemet. Med andre ord, kan den abstrakte matematisk
analyse bruges til at give en præcis mening til begreber som ret linje, plan, vinkel, osv.

Det Euklidiske rum.

Vi starter med at organisere planen $\mathbb{R}^2$ som et vektorrum hvor hvert punkt r er entydigt beskrevet af to reelle koordinater x og y, eller r = [x; y]. Rummet $\mathbb{R}^2$ er samtidig et Hilbertrum genereret af det euklidiske indre produkt, og det gør i sidste ende, at afstanden mellem to punkter r = [x; y] og r’ = [x’; y’] er givet ved Pythagoras’ formel:

$|\mathbf{r}-\mathbf{r}'|=\sqrt{(x-x')^2+(y-y')^2}.$
Hvis vi har en kurve i planen defineret ved r(t) = [x(t); y(t)] hvor både x(t) og y(t) er
differentiable funktioner, så definerer vi buelængden mellem punkterne r(t_0) og r(t_1) som:

$L(t_1,t_0):=\int_{t_0}^{t_1} \sqrt{(x'(t))^2+(y'(t))^2}dt$
Tag nu et stykke papir frem og vælg et vilkårligt punkt O. Papiret modellerer $\mathbb{R}^2$ mens O svarer til punktet [0; 0]. Vælg nu et andet vilkårligt punkt $P \neq O$ pa papiret og kald det [1; 0].

På denne måde bestemmer vi også hvad det betyder at have “længde en” i vores model.
x-aksen bliver nu den rette linje som forbinder O med P. Set som et underrum af
dimension 1, består vores x-akse af alle punkterne af typen [t; 0] hvor $t\in\mathbb{R}$ . Vi er nu klar til at gå i gang med at finde punktet med koordinater [0; 1] og derefter at tegne y-aksen.

Cosinus og sinus.

Betragt systemet af differentialligninger $f'(t) = -g(t)$ og $g'(t) = f(t)$ , hvor f(0) = 1
og g(0) = 0. Den generelle teori omkring førsteordens lineære differentialligninger med
en global Lipschitz betingelse garanterer, at der findes en entydig global løsning til vores
ligningsystem.

Lad os nu udlede nogle vigtige egenskaber ved f og g.
1. Funktionen $h(t) = f^2(t) + g^2(t)$ må være konstant, fordi $h'(t) = 0$ for alle t, og derfor har vi, at $h(t) = f^2(t) + g^2(t)$ = $h(0) = 1$ for alle t. Vi konkluderer, at billedmængden af kurven r(t) = [f(t); g(t)] er en delmængde af enhedscirklen.

2. Nu viser vi, at $f$ og $g$ er periodiske. Vi ved, at $-1\leq f(t)\leq 1$ og $-1\leq g(t)\leq 1$ . Når $t$ bliver kun lidt større end 0, er $f(t)$ stadigvæk tæt på 1, derfor positiv. Ligningen $g'(t)=f(t)$ medfører til, at $g$ vokser og bliver større end nul. Samtidig har vi fra $f'(t)=-g(t)<0$ , at $f$ er aftagende og bliver mindre. Det må derfor eksistere et $t_1>0$ sådan at $f(t_1)=0$ og $g(t_1)=1$ .

Når $t$ er lidt større end $t_1$ , bliver $f$ negativ og aftagende mod $-1$ mens $g$ forbliver positiv men aftager mod $0$ . Det må eksistere et $t_2>t_1$ sådan at $f(t_2)=-1$ og $g(t_2)=0$ .

Når $t$ er lidt større end $t_2$ bliver $g$ negativ og aftagende mod $-1$ mens $f$ er negativ og voksende mod $0$ . Det må eksistere et $t_3>t_2$ sådan at $f(t_3)=0$ og $g(t_3)=-1$ .

Endelig, når $t$ er lidt større end $t_3$ , er $g$ negativ og voksende mod $0$ mens $f$ er positiv og voksende mod $1$ . Det må eksistere et $T>t_3$ sådan at $f(T)=1$ og $g(T)=0$ .

En vigtig konsekvens er, at funktionerne $\tilde{f}(t):=f(t+T)$ og $\tilde{g}(t):=g(t+T)$ løser det samme system som $f$ og $g$ , og har de samme begyndelsesværdier. Løsnings entydighed medfører derfor til, at $f(t)=f(t+T)$ og $g(t)=g(t+T)$ . Det beviser, at $f$ og $g$ er periodiske og tallet $T$ er den mindste (positive) periode. Fra nu af, ændrer vi $f$ ‘s navn til $\cos$ , $g$ ‘s navn til $\sin$ , og skriver $2\pi$ i stedet for $T$ .

3. Definer $u(t):=\cos^2(t/2)-\sin^2(t/2)$ og $v(t):=2\cos(t/2)\sin(t/2)$ . Vi har, at $u'=-v$ og $v'=u$ samt med $u(0)=1$ og $v(0)=0$ . Løsningens entydighed medfører igen at $u(t)=\cos(t)$ og $v(t)=\sin(t)$ . Med andre ord:

$\cos(t)=\cos^2(t/2)-\sin^2(t/2),\quad \sin(t)=2\cos(t/2)\sin(t/2).$

4. Vi skal nu vise, at $t_1=\pi/2$ , $t_2=\pi$ og $t_3=3\pi/2$ . Husk, at $t_1$ er det mindste positive tal hvor $\cos(t_1)=0$ og $\sin(t_1)=1$ , $t_2$ er det mindste positivt tal hvor $\cos(t_2)=-1$ og $\sin(t_2)=0$ , mens $t_3$ er det mindste positivt tal hvor $\cos(t_3)=0$ og $\sin(t_3)=-1$ . Perioden $T=2\pi$ er det mindste positivt tal hvor $\cos(T)=1$ og $\sin(T)=0$ .

Hvis vi indsætter $t=2\pi$ i ligningen ovenfor, har vi at:

$0=\sin(2\pi)=2 \cos(\pi) \sin(\pi),\quad 1=\cos(2\pi)=\cos^2(\pi)-\sin^2(\pi).$

Den første ligning kræver, at enten $\cos(\pi)$ eller $\sin(\pi)$ må være nul. Hvis vi kobler det med den anden ligning, konkluderer vi, at $\sin(\pi)=0$ og $\cos(\pi)=\pm 1$ . Men $\cos(\pi)$ kan ikke være lig med $+1$ fordi $\pi<T=2\pi$ og $T$ er det mindste positiv tal hvor systemet vender tilbage til begyndelsesværdien. Derfor er $\cos(\pi)=-1$ og $\sin(\pi)=0$ , og ud fra definitionen af $t_2$ må vi have, at $t_2=\pi$ .

Definer $u(t):=-\cos(\pi-t)$ og $v(t):=\sin(\pi-t)$ . Vi ser, at $u'=-v$ og $v'=u$ samt med $u(0)=1$ og $v(0)=0$ . Så har vi, at $u(t)=\cos(t)$ og $v(t)=\sin(t)$ . Eller:

Ligning 3 $\cos(t)=-\cos(\pi-t),\quad \sin(t)=\sin(\pi-t).$

Indsæt $t=\pi/2$ i ligningen ovenfor. Det giver $\cos(\pi/2)=-\cos(\pi/2)$ , eller $\cos(\pi/2)=0$ . Men det eneste punkt mellem $0$ og $t_2=\pi$ hvor cosinus kan være nul er $t_1$ . Derfor har vi, at $t_1=\pi/2$ , og $\sin(\pi/2)=\sin(t_1)=1$ .

Vi skal vise nu, at $t_3=3\pi/2$ . Definer $u(t):=\cos(-t)$ og $v(t):=-\sin(-t)$ . Igen igen $u'=-v$ , $v'=u$ , $u(0)=1$ og $v(0)=0$ . Så har vi, at:

Ligning 4 $\cos(t)=\cos(-t),\quad \sin(t)=-\sin(-t).$

Indsæt $t=-\pi/2$ i Ligning 3 og brug Ligning 4:

$0=\cos(\pi/2)=\cos(-\pi/2)=-\cos(3\pi/2),\quad -1=-\sin(\pi/2)=\sin(-\pi/2)=\sin(3\pi/2).$

Hvor stort er $\pi$ ?

Tangensfunktionen defineres som $\tan(t)=\frac{\sin(t)}{\cos(t)}$ for $-\pi/2<t<\pi/2$ . På det interval har vi, at $\tan'(t)=\frac{1}{\cos^2(t)}>0$ , funktionen er bijektiv og billedmængden er $\mathbb{R}$ . Dens inverse noteres med $\arctan$ , er defineret på $\mathbb{R}$ med værdier i $(-\pi/2,\pi/2)$ , og $\arctan'(x)=\frac{1}{1+x^2}$ .

Indsæt $t=\pi/2$ i Ligning 2. Vi ser, at $\sin(\pi/4)=\cos(\pi/4)=1/\sqrt{2}$ og $\tan(\pi/4)=1$ og $\arctan(1)=\pi/4$ . Derfor:

$\pi= 4\int_0^1 \arctan'(x)dx=4 \int_0^1 \frac{1}{1+x^2}dx.$

Taylors formel med restled medfører til:

$1-y+\ldots -y^{2n+1}$ $<\frac{1}{1+y}<1-y+\ldots +y^{2n},\quad n\geq 0,\quad y>0,$

og hvis $y=x^2$ :

$1-x^2+\ldots -x^{4n+2}<\frac{1}{1+x^2}<1-x^2+\ldots +x^{4n}.$

Efter integration mellem $0$ og $1$ :

$4\sum_{k=0}^{2n+1} \frac{(-1)^k}{2k+1} <\pi <4\sum_{k=0}^{2n} \frac{(-1)^k}{2k+1},\quad n\geq 0.$

Det definerer en konvergent række, og ved hjælp af det kan vi komme arbitrært tæt på $\pi$ . I hvert fald, er $\pi$ mindre end $4$ . Rækken blev først fundet omkring 1400 tallet af den indiske matematiker Madhava fra Sangamagrama, og senere genfundet af James Gregory i 1668.

Tegning af y-aksen.

Nu er vi næsten klar til at tegne vores y-akse. Betragt kurven $\mathbf{r}(t)=[\cos(t),\sin(t)]$ . Vi har lige set, at når $t$ varierer fra 0 til $2\pi$ , dækker vi hele enhedscirklen. Buelængden fra $\mathbf{r}(0)=[1,0]$ til $\mathbf{r}(\theta)$ hvor $\theta \leq 2\pi$ er givet ved formlen 1. Her husker vi igen, at $x'(t)=-y(t)$ , $y'(t)=x(t)$ , $x^2(t)+y^2(t)=1$ og derfor $(x'(t))^2+(y'(t))^2=1$ . Det giver:

$L(0,\theta)=\theta,\quad L(0,\pi)=\pi.$

Tag nu en passer og tegn cirklen med origo i $O$ og som går gennem $P=[1,0]$ . Cirklen krydser igen x-aksen i punktet $\mathbf{r}(\pi)=[-1,0]$ . Tag et stykke snor af længde $4$ og dæk den del af cirklen hvor $y>0$ , og med et endepunkt i $\mathbf{r}(0)$ . Vi har vist, at $\pi<4$ , så er snoren lang nok til at nå punktet $\mathbf{r}(\pi)$ . Klip snoren således at et af stykkerne dækker den øvre halvcirkel fra $\mathbf{r}(0)$ til $\mathbf{r}(\pi)$ . Vi ved, at længden af stykket må være lig med $\pi$ . Del snoren i to og sæt en halvdel af den tilbage på cirklen med et endepunkt i $\mathbf{r}(0)$ . Halvdelen er nu kun $\pi/2$ lang, så må det andet endepunkt ligge på $\mathbf{r}(\pi/2)=[0,1]$ . Tegn y-aksen og drik en stor, sort kaffe.

Tallet $\pi$ er irrationalt.

Ja, det ved jeg godt. De moderne, pengefikserede tider vi lever i, er i mindre grad egnede til rene matematiske spørgsmål som irrationaliteten af et mærkeligt tal som $\pi$ . Men alligevel: dem som har nået at læse hertil må have haft en ærlig interesse i matematik, derfor skal jeg bare fortsætte uanset hvad.

Jeg skal tage udgangspunkt i Ivan Nivens artikel “A simple proof that $\pi$ is irrational”, Bull. Amer. Math. Soc. 53(6), 509 (1947). Vi skal vise, at $\pi$ ikke kan skrives som en brøk $a/b$ hvor $a$ og $b$ er begge heltal. Men lad os antage det modsætte; det vil sige, vi antager at $\pi=a/b$ hvor $a$ og $b$ er heltal.

Vi definerer to polynomier:

$p_n(x)=\frac{1}{n!}x^n(a-bx)^n,\quad P_n(x)=p_n(x)-p_n''(x)+\ldots+(-1)^n p_n^{(2n)}(x),\quad n\geq 1.$

Lad os nu vise, at alle tal af typen $p_n^{(j)}(0)$ er heltal. For eksempel, har vi at:

$p_n'(x)=\frac{1}{n!}(nx^{n-1}(a-bx)^n-nbx^n(a-bx)^{n-1})=\frac{1}{(n-1)!}x^{n-1}(a-bx)^{n-1}(x-b(a-bx)).$

Vi ser, at $p_n'(0)$ er nul hvis $n>1$ og $p'_1(0)$ $= a$ hvis $n=1$ . Hvis vi fortsætter med at differentiere, finder vi, at $p_n^{(j)}(0)$ er altid nul hvis $j<n$ , mens når $j\geq n$ , er de eneste ikke nul bidrag fra de forskellige led kun dem hvor vi har “differentieret væk” faktoren $x^n$ . Det giver en $n!$ som gør, at resultatet bliver et heltal.

Vi bemærker identiteten $p_n(x)=p_n(a/b-x)$ . Kædereglen siger, at $p_n^{(j)}(a/b)=(-1)^jp_n^{(j)}(0)$ , derfor er $p_n^{(j)}(\pi)$ også heltal, for alle $j\geq 1$ . En vigtig konsekvens er, at både $P_n(0)$ og $P_n(\pi)$ er heltal.

Ud fra definitionen af $P_n(x)$ ser vi, at $P_n''(x)+P_n(x)=p_n(x)$ . Derfor:

$(P_n'(x)\sin(x)-P_n(x)\cos(x))'= P_n''(x)\sin(x)+P_n(x)\sin(x)=p_n(x)\sin(x).$

Analysens fundamentalsætning medfører til:

$\int_0^\pi p_n(x)\sin(x)dx =P_n(\pi)+P_n(0),$

hvor højresiden altid er et heltal, for alle $n$ . Funktionen $p_n(x)\sin(x)$ er altid positiv på intervallet $(0,\pi)$ , derfor er dens integral også positiv ved siden af at være et heltal. Vi må have:

$1\leq \int_0^\pi p_n(x)\sin(x)dx, \quad {\rm for} \; {\rm all}\; n\geq 1.$

På den anden side, er $p_n(x)\sin(x)\leq \frac{ \pi^n a^n}{n!}$ når $0<x<\pi$ . Derfor, $1\leq \int_0^\pi p_n(x)\sin(x)dx\leq \frac{ \pi^{n+1} a^n}{n!}$ . Men højresiden går mod nul når $n$ vokser, og her er vores modstrid.

Hvordan kan man regne på/med information, man ikke kan se?

Ignacio Cascudo er adjunkt på instituttet her har skrevet et rigtig godt blogindlæg om, hvordan man kan ræsonnere om og regne på/med information, man ikke kan “se”. Jeg har ikke oversat det – mon ikke I kan klare at læse det på engelsk?

How to compute on information you don’t see.

Information security, and in particular cryptography, is a very popular topic nowadays. People are concerned about the privacy of their sensitive information, such as their economic situation, health, or other issues.

It is fair to say that, when we speak about cryptography, what comes to mind to most people is the subject of encryption: how to transmit a message to some other person so that if someone intercept that message, he/she will not be able to read it; you may also know about another cryptographic topic: digital signatures, which allow to prove (authenticate) that certain person is the author of a message and that it has not been modified after being signed and sent.

But cryptography also includes the study of other problems that you may not be aware of; and yet, they are really surprising, and have very important applications, which are becoming more and more popular.

-Do you know for example that using cryptographic tools you can have two parties find out who of the two is richer, or older, or heavier without any of them having to reveal (to the other person or to anybody else) his/her actual wealth, or age, or weight? This can be used for “benchmarking”, where two or more companies can compare these results and find out their weaker points with respect to the competition, without needing to reveal precisely how well or bad they are doing.

-Or that you can run an auction among several people, where everyone of them want to bid some amount for an item and determine who wins the bid without needing to reveal the bids of the losers? This can be used for automatic bidding for ads in the internet. Another scenario where this was used in a pioneer work, carried out in Denmark by researchers of Aarhus University, is the trading of sugar beet prices between the company Danisco and farmers.

-Or that you can run a voting with several voters so that none of them has to ever reveal their vote to anybody, yet at the end of the day, all of them know exactly the result of the voting? And you don’t need ballots for this, in principle you could do it by having each pair of voters exchange messages with each other privately.

These kind of problems is what the subject of secure multiparty computation is concerned with. Secure multiparty computation deals with the scenario where two or more parties want to jointly make some calculation involving private data held by some of them, but without actually revealing this data, they only want to reveal the outcome of the computation.

Since the spectrum of applications is very broad, different solutions and techniques are used for the different scenarios.

Voting

A simplified example of a multiparty computation scenario, where we can show an easy solution, is the following: imagine Alice, Bob and Charlie want to compute the result of a voting, where there are two possible votes (yes or no) and we want to count the number of yes votes. So if we assign number 1 to ‘yes’ and number 0 to ‘no’, we just need to compute the sum of what Alice, Bob and Charlie vote. But now, how can this be computed without having Alice, Bob or Charlie communicate their votes to anybody? Here is a sequence of steps (what is usually called “a protocol”) that can accomplish this goal:

Each party selects three 1-digit numbers such that the sum of these numbers has his/her vote as its last digit. For example if Alice wants to vote yes, she could choose the numbers 2,4 and 5 since 2+4+5=11, and the last digit of 11 is a 1 (which means yes). She could also choose 7,7,7 (the numbers do not need to be different), since 7+7+7=21, or 0,0,1, since 0+0+1=1.
If she voted no, she could have chosen for example 6,5,9 since 6+5+9=20.
Simultaneously, Bob and Charlie do the same with their votes they have.
Each party takes the three numbers he/she has generated in step 1., and sends a different one to each other party (including keeping one for him/herself).
So, if for example Alice has chosen (2,4,5), she sends the value 4 to Bob, 5 to Charlie and keeps the value 2 for herself.
In the next step, each of the players sum the elements he/she has received (including the one he/she kept for him/herself).
Finally each of the players announces publicly the last digit of the sum each one has computed. The results are in turn summed and the last digit of the sum is the final result of the voting.

The table below represents a voting situation: the votes are in blue. The entry corresponding to e.g. Alice row and Bob column is the number Alice has sent to Bob (4, in this example); the entry corresponding to Alice row and column is the number she has generated and kept for herself (2 in this case).

$Voting$

The last values in each column correspond to the sum of the values received by each player (e.g. 15=2+7+6 for Alice), of which each announces publicly the last digit. The sum of these announced digits (which is 12 in this example) is therefore a public value, of which the last digit 2, is the number of yes votes.

This protocol always gives the correct sum of the votes and, almost magically, the vote is private in the sense that the vote of each player remains hidden from the others.

At this point you may complain: “but, that cannot be true, because consider Bob; he voted no (0) and the result was 2 yes votes, so he does know the votes from the other players have to be yes”. This is true; however, it is unavoidable: since the outcome has to be public, no matter how we do the voting (by a multiparty computation protocol, with the help of some trusted mediator or in any other possible solution) Bob would know that Alice and Charlie voted yes. What multiparty computation protocols have to deal with, is to avoid that other information is leaked: for example, since Alice has voted yes, and the was result was 2 yes votes, she should have no information about whether the other yes-voter was Bob or Charlie.

But how could one even be sure about this?. The key is that one can imagine this alternative situation:

$votes2$

The information seen by Alice (her row and column, the announced values and the vote outcome) is exactly the same in this case as in the one above, yet in the case above it was Bob who voted yes, while in the situation below the yes-voter was Charlie. For Alice, it is as solving a Sudoku that has two solutions and each of the solutions leads to a different guess about who is the other yes-voter.

But what happens if a player tries to cheat, sending wrong information (for example vote “2”)? Or if a player refuses to continue with the protocol at some point? And how do you compute functions more complicated than sums? Many different tools involving different mathematics are needed to address all these problems, with fancy names such as oblivious transfer, commitment schemes, secret sharing or zero knowledge proofs (cryptographers are good at baptising their tools). One interesting tool from the mathematics point of view is secret sharing.

Secret sharing

At the beginning of the protocol above, Alice, Bob and Charlie distribute their votes among each other, in such a way that no single person knows the vote of anyone else.

This technique of distributing information is called secret sharing, and can be used for other goals too: for example, if you want to store some important information (a “secret”) but you are afraid to leave it in one place, where it could be potentially accessed by someone you don’t trust; in that case, you could think of distributing the information across several locations (e.g. several hard disks). Secret sharing even allows to do it in such a way that you can share a secret among, say, 4 computers so that if the information stored in 2 of them is accessed, the secret is kept completely hidden; but on the other hand you can recover the secret if you can access any 3 out of the 4 computers (so if one of them crashes you still don’t lose the secret).

The most popular secret sharing scheme was invented by Adi Shamir (the same Shamir that invented the RSA cryptosystem together with Ron Rivest and Leonard Adleman) and it uses properties of evaluations of polynomials. It is in fact based on the same ideas as another tool of discrete mathematics known as “Reed-Solomon error correcting code”, used for the reliable and efficient transmission of information through channels with noise.

The idea is that if you are given a number of evaluations of a polynomial (for example you know that f(3)=9, f(2)=5 and f(1)=3) there is exactly one polynomial of small degree that satisfies these evaluations. “Low degree” means “less than the number of evaluations”. So in the case above, since you are given 3 evaluations, there is one possible polynomial of degree at most 2 that satisfies the conditions, which is in fact x²-x+3. One can reconstruct this polynomial using so-called Lagrange interpolation.

This is still valid if, instead of using real numbers, one works over another field, and in the case of secret sharing calculations are usually performed over finite fields (which were already explained in Turingprisen til Diffie og Hellman on the blog here.)

In Shamir’s secret sharing scheme each of the players is given the evaluation in a different point of a hidden polynomial of degree at most t. The secret is actually the evaluation of the polynomial in another different point, say for example, the point 0.

Now if t+1 participants meet and pool together the shares they have receive, they together know t+1 different evaluations of f, and then they can determine the polynomial, since we know it has degree at most t. But t players together will be missing one evaluation point, and in fact for every element of the field there will be exactly one polynomial consistent with the information they know and that yields this element as secret.

$polynomials$

This picture shows several polynomials of degree 2 consistent with the same 2 evaluations. If we have taken t=2 in the explanation above, the set of 2 players who know these 2 evaluations, will not be able to know the secret, since each of the possible polynomials of degree at most 2 leads to a different evaluation in 0. Source:wikipedia

Andre gode blogs – jo, de findes…

Bloggen her er naturligvis den bedste i hele Verden, men der findes andre matematikblogs, som jeg i øvrigt lader mig kraftigt inspirere af ind imellem. Her er nogle eksempler – måske kan der være ideer til blogindlæg, som I kan bede om/foreslå. Jeg holder mig her til blogs på engelsk eller dansk.

Den amerikanske (forstået som USA) matematiske forening, AMS, har flere blogs, herunder en Blog on math blogs.

Quanta Magazine er ikke en blog, men en imponerende samling artikler om både matematik og anden videnskab. De har en blog, Abstractions.

The Aperiodical er “et mødested for folk, der kan lide matematik og gerne vil vide mere”. Tre hovedforfattere, som har hver deres stil og interesse. De organiserer en opsummering af andre matematikblogs under overskriften Carnival of Mathematics. Det er andre blogs, der skiftes til at lave dette overblik, men der linkes fra the Aperiodical.

Plus Magazine formidler på et lidt lavere niveau end de ovenstående. Og det er strengt taget ikke en blog…

Sandsynligvis.dk er en dansk blog om sandsynligheder og statistik. Søren Højsgaard er en af forfatterne.

Og mange, mange flere, men nu har I nok at klikke rundt i. Finder man Terry Taos blog eller Timothy Gowers’ blog, har de alenlange “blogrolls” med links til andre matematikblogs.

Olympisk matematik. Mest om orden.

Det er olympiadetid og matematikeren tænker helt ærligt ikke meget på matematik, når hun ser OL, men alligevel sniger det sig ind. På Det britiske “Millenium Math Project” lavede de op til OL i London en stor indsats for at bringe matematik og sport ud til skolerne. Der er mange ideer, som jeg da kan forestille mig, danske skoler, herunder gymnasierne, kunne have fornøjelse af. KS5 er Key Stage 5, som er omkring 2g og artikler retter sig mod det niveau og højere.

Hvilke lande klarer sig bedst til OL? Et simpelt spørgsmål, men der er ikke et entydigt svar. For hvad mener man med bedst? I en ranking er Danmark lige nu nummer 33, men vi kan også være nummer 17. Nummer 17 bliver vi i den lettest forståelige ranking, nemlig det totale antal medaljer, mens vi er nummer 33, når man i linket ovenfor klikker på guldmedaljer. Faktisk er det ikke kun guldmedaljer, men en orden, hvor man først ser på antal guldmedaljer, dernæst sølv og dernæst bronze. Iran har 2 guld, 0 sølv, 1 bronze og ligger altså højere end Danmark, som har 1 guld, 3 sølv og 4 bronze. Sverige har 1 guld, 4 sølv og 1 bronze og ligger derfor højere end Danmark.

Data for hvert land er 3 tal eller et punkt i rummet (guld, sølv, bronze) og en ranking er noget 1-dimensionalt. Så man smider noget information væk. Det totale antal medaljer som ranking, guld+sølv+bronze, kan betragtes som en ranking via funktionen f(x,y,z)=x+y+z, altså $(g1,s1,b1)\geq (g2,s2,b2)$ hvis $f(g1,s1,b1)\geq f(g2,s2,b2)$ og så er der jo frit slag: Vælg en funktion $h:\mathbb{R}^3\to \mathbb{R}$ og brug ordningen af de reelle tal til at ordne punkter i rummet. Man vil jo nok kræve noget af funktionen h. Eksempelvis, at lande med lige mange guld og bronze, men forskelligt antal sølv bliver ranket efter, hvem der har flest sølvmedaljer.

Og nej, jeg siger ikke, at alle ordner giver mening – man skulle jo nødig lægge sig ud med nogen:

$XKCD om for meget matematik og stangspring...$

XKCD om for meget matematik og stangspring…

Ordningen efter først guld, så sølv og dernæst bronze er en leksikografisk orden. Det svarer til at sætte ord i alfabetisk orden, hvor første bogstav bestemmer mest, dernæst andet bogstav etc. Er der mon en funktion som ovenfor, der svarer til leksikografisk orden? Ja da. En ranking ER jo en funktion til de naturlige tal og dermed de reelle tal. Så spørgsmålet skal formuleres om, hvis det skal være interessant. Er der en lineær funktion f(x,y,z)=Ax+By+Cz, som giver leksikografisk orden? Ja og nej må svaret vist være. Jeg har lige vendt det med Hans Hüttel og vi konkluderer, at for OL med endelig mange medaljer kan man godt lave sådan en lineær funktion. Ja ja, jeg ved det godt. OL har ikke uendelig mange medaljer, men matematikere forsøger altid at tænke mere generelt over den slags. Så her kommer svaret med Ja:

Lad os bruge medaljerne fra London som udgangspunkt. Der blev uddelt 300 guld, 305 sølv og 356 bronze. Der gives eksempelvis 2 bronze i hver vægtklasse i taikwondo, judo, boksning og brydning og så var der nogen, der hoppede, løb, svømmede præcis lige højt, længst, hurtigt og derfor gav anledning til flere medaljer af samme metal. Nå, men uanset dette: Hvis vi nu bruger funktionen f(g,s,b)= 20.000g+500s+b og derefter bruger ordenen på de reelle tal, så vil en guldmedalje være mere værd end alle sølvmedaljer plus alle bronzemedaljer og en sølv vil være mere værd end alle bronze. Voila. Der er naturligvis mange muligheder for funktionen f. Mulighederne er begrænset som følger: f(g,s,b)=Ag+Bs+Cb skal opfylde (punkt 3 skal læses før 1 og 2 – jeg bruger den betingelse under argumentationen for 1 og 2)

Hvis g1>g2 er f(g1,s1,b1)>f(g2,s2,b2). Altså $Ag_1+Bs_1+Cb_1>Ag_2+Bs_2+Cb_2$ eller omskrevet $A(g_1-g_2)>B(s_2-s_1)+C(b_2-b_1)$ . Worst case (eller med matematik, det, der vil medføre, at uligheden holder i alle andre situationer) må være g1=g2+1, s1=b1=0 og s2 og b2 maksimale (landet har vundet alle sølv og alle bronze…) Altså kræves $A>Bn_s+Cn_b$ , hvor $n_s$ er det totale antal sølvmedaljer og $n_b$ det totale antal bronze.
Hvis $g_1=g_2$ og $s_1>s_2$ er f(g1,s1,b1)>f(g2,s2,b2), som igen er $Ag_1+Bs_1+Cb_1>Ag_2+Bs_2+Cb_2$ . Eftersom der er samme antal guldmedaljer, reducerer uligheden til $B(s_1-s_2)>C(b_2-b_1)$ og igen er der et worst case, nemlig hvor s1=s2+1 og b2 er maksimalt. Det giver $B>Cn_b$ .
A,B og C skal være positive tal, da eksempelvis b1>b2 skal give f(0,0,b1)>f(0,0,b2) etc.

For OL med uendeligt mange medaljer kan leksikografisk orden ikke fremkomme ved at vælge en lineær funktion på den måde. Hvorfor? Jo, antag, at funktionen f kan bruges til det. Så er f(1,0,0) et tal, som skal være større end f(0,0,k) for alle k. Hvis f er lineær og A,B,C er positive, kan det ikke lade sig gøre.

Jo, men Danmark er et lille land. Det må tælle med i ranking. Det har de kigget på hos Milleniium Project og de har også set på BNP – er man et rigt land, har man råd til at bygge svømmebassiner og den slags. Så kan man spørge, om lande har klaret sig bedre end forventet udfra befolkningens størrelse og BNP.

Der er endda nogen, der har skrevet en artikel Who wins the Olympic Games: Economic development and medal totals De har formler for antal medaljer for et land. En smule skepsis er på sin plads – jeg har ikke set på, om formlerne giver det rigtige antal medaljer i London, men mon dog. Der er i hvert fald mange konstanter, man skal have fastsat. For eksempel indgår, om landet er en tidligere sovjetstat. Og om de har planøkonomi….

Og så lige et lille host: Hvis universiteter blev rankede leksikografisk, så ville Aalborg godt nok ligge højt på listen. Eller langt nede, hvis Aa er sidst i alfabetet…